概率与统计-方差、协方差和协方差矩阵

方差(Variance)：方差是标准差(Standard deviation)的平方，而标准差的意义是数据集中各点到均值点距离的平均值。反应的是数据的离散程度。假设$X$是一个随机变量，则方差可以表示为：

$$var(X) = E[(X-E(X))(X-E(X))]=E[(X-E(X))^2]$$

其中，$E(X)$是随机变量$X$的期望。

协方差(Covariance)：标准差与方差是描述一维数据的，当存在多维数据时，我们通常需要知道每个维数的变量之间是否存在关联。协方差就是衡量多维数据集中变量之间相关性的统计量。比如说，一个人的身高与他的体重的关系，这就需要用协方差来衡量。如果两个变量之间的协方差为正值，则这两个变量之间存在正相关，若为负值，则为负相关。

协方差的意义：在概率论中，两个随机变量$X$与$Y$之间的相互关系，大致有下列3种情况：

1）当$X$，$Y$的联合分布像图(2.1)那样时，我们可以看出，大致上有：$X$越大$Y$也越大，$X$越小$Y$也越小，这种情况，我们称为“正相关”。

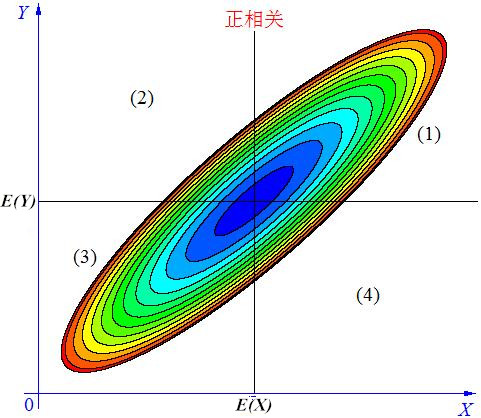
图2.1 随机变量X与Y正相关

2）当$X$，$Y$的联合分布像图(2.2)那样时，我们可以看出，大致上有：$X$越大$Y$反而越小，$X$越小$Y$反而越大，这种情况，我们称为“负相关”。

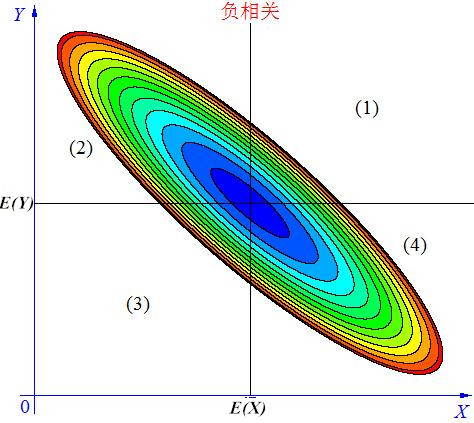
图2.2 随机变量X与Y负相关

3）当$X$，$Y$的联合分布像图(2.3)那样时，我们可以看出，大致上有：既不是$X$越大$Y$也越大，也不是$X$越大$Y$反而越小，这种情况我们称为“不相关”。

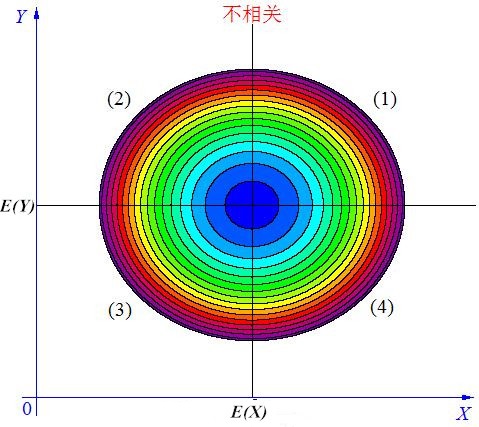
图2.3 随机变量X与Y不相关

那么，怎样将这3种相关情况，用一个简单的数学表达式表达出来呢？观察上面3种情况的图可以看出：

  1）在3幅图的区域（1）中，有$X \gt E(X)$， $Y-E(Y) \gt 0$，所以$(X-E(X))(Y-E(Y)) \gt 0$；
  2）在3幅图的区域（2）中，有$X \lt E(X)$， $Y-E(Y) \gt 0$，所以$(X-E(X))(Y-E(Y)) \lt 0$；
  3）在3幅图的区域（3）中，有$X \lt E(X)$， $Y-E(Y) \lt 0$，所以$(X-E(X))(Y-E(Y)) \gt 0$；
  4）在3幅图的区域（4）中，有$X \gt E(X)$， $Y-E(Y) \lt 0$，所以$(X-E(X))(Y-E(Y)) \lt 0$。

所以很直观地看：

当$X$与$Y$正相关时，它们的分布大部分在区域（1）和（3）中，小部分在区域（2）和（4）中，所以平均来说，有$E[(X-E(X))(Y-E(Y))] \gt 0$;
当$X$与$Y$负相关时，它们的分布大部分在区域（2）和（4）中，小部分在区域（1）和（3）中，所以平均来说，有$E[(X-E(X))(Y-E(Y))] \lt 0$;
当$X$与$Y$不相关时，它们的分布在区域（1）和（3）中，与（2）和（4）中的几乎一样多，所以平均来说，有$E]X-E(X))(Y-E(Y)]=0$。

所以，我们可以定义一个表示$X$， $Y$相互关系的数字特征，也就是协方差：

$$cov(X, Y) = E[(X-E(X))(Y-E(Y))]$$

当$cov(X, Y) \gt 0$时，表明$X$与$Y$正相关；
当$cov(X, Y) \lt 0$时，表明$X$与$Y$负相关；
当$cov(X, Y) = 0$时，表明$X$与$Y$不相关。

这就是协方差的意义。

协方差矩阵，当变量多了，超过两个变量了。那么，就用协方差矩阵来衡量多变量之间的相关性。假设$X$是以$n$个随机变数（其中的每个随机变数也是一个向量，当然是一个行向量）组成的列向量：

$X = \left[\begin{matrix}X_1 \\ X_2 \\ \vdots \\ X_n \end{matrix}\right]$

其中，$\mu_i$是第$i$个元素的期望值，$i=1, 2, \dots , n$，即$\mu_i=E(X_i)$。协方差矩阵的第$i$，$j$项(第$i$，$j$项是$X_i$，$X_j$的协方差)被定义为如下形式：

$$\sum_{ij} = cov(X_i, X_j) = E[(X_i-\mu_i)(X_j-\mu_j)]$$

则协方差矩阵可以表示为：

$\sum = \left[\begin{matrix}E[(X_1-\mu_1)(X_1-\mu_1)] & E[(X_1-\mu_1)(X_2-\mu_2)] & \cdots &E[(X_1-\mu_1)(X_n-\mu_n)] \\ E[(X_2-\mu_2)(X_1-\mu_1)] & E[(X_2-\mu_2)(X_2-\mu_2)] & \cdots &E[(X_2-\mu_2)(X_n-\mu_n)]\\ \vdots & \vdots & \ddots & \vdots\\ E[(X_n-\mu_n)(X_1-\mu_1)] & E[(X_n-\mu_n)(X_2-\mu_2)] & \cdots &E[(X_n-\mu_n)(X_n-\mu_n)] \end{matrix}\right]$

那么，协方差矩阵中的元素对数据的分布有什么影响呢？

首先，我们来看看一维正态分布随机变量的分布与均值$\mu$和$\sigma$的关系，如图(2.4)所示：

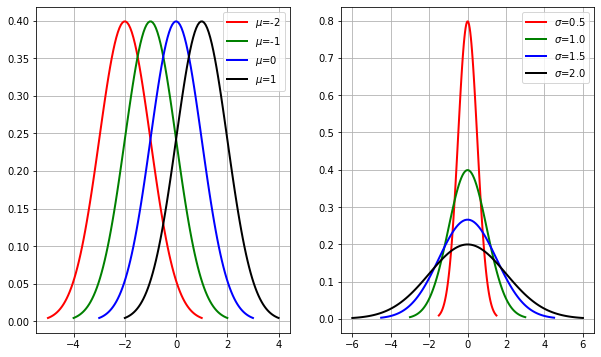
图2.4 一维正态分布随机变量的分布与均值和方差的关系

可以看出：
  1）均值决定了分布的中心点位置
  2）方差决定了分布图形的形状是“胖”（圆）还是“瘦”（扁）

接下来，协方差矩阵中的元素对数据的分布影响，以二维正态分布为例，其中包含3个不同取值的均值(向量)和协方差矩阵：
1）3组数据的协方差矩阵相同，都为对角阵，对角线元素相同，如图（2.5）：

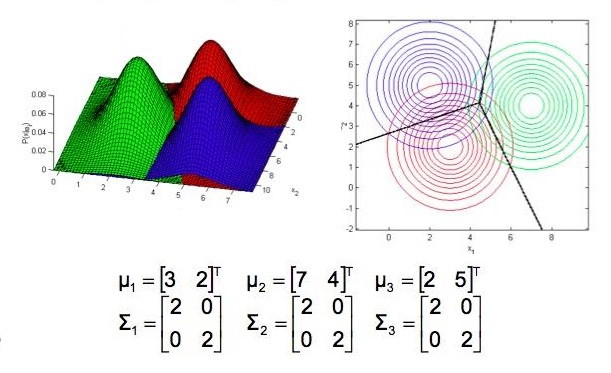
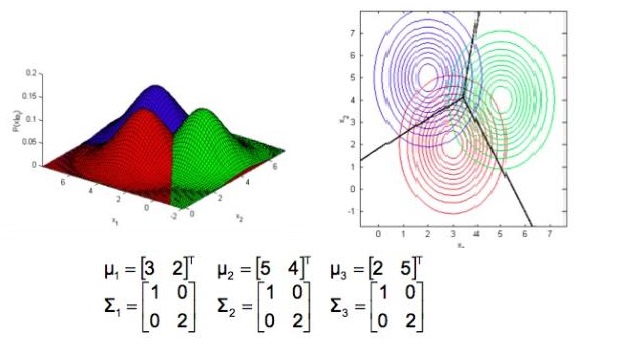
图2.5 2）3组数据的协方差矩阵相同，都为对角阵，对角线元素不同，如图（2.6）：
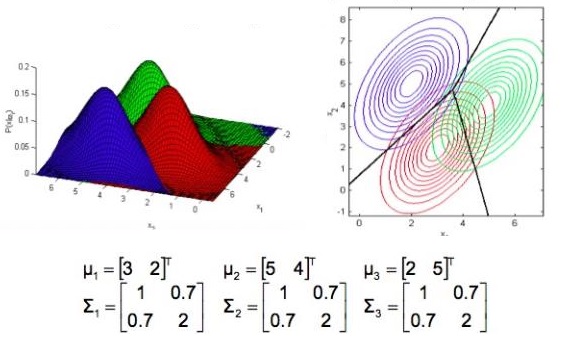
图2.6 3）3组数据的协方差矩阵相同，不是对角阵，对角线元素不同，如图（2.7）：
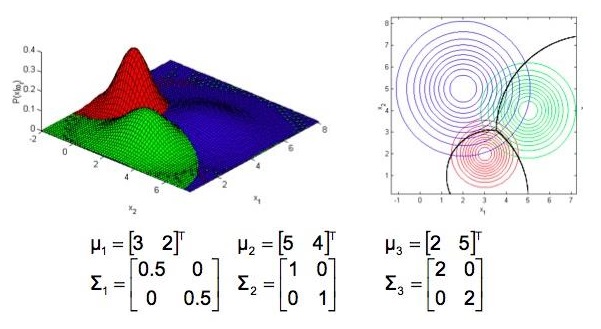
图2.7 4）3组数据的协方差矩阵不同，都是对角阵，对角线元素相同，如图（2.8）：
图2.8 5）3组数据的协方差矩阵不同，不是对角阵，对角线元素不同，如图（2.9）：
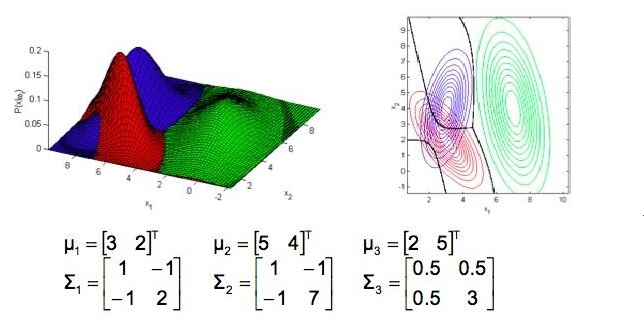
图2.9

可以看出：

  1）均值为分布的中心点位置。
  2）对角线元素决定了分布图形是圆还是扁。
  3）非对角线元素决定了分布图形的轴向（扁的方向）。

参考来源：
1）https://www.jianshu.com/p/5706a108a0c6