机器学习笔记-距离度量与相似度(一)闵可夫斯基距离

在机器学习过程中，我们经常需要知道个体(样本)之间的差异大小，进而评价个体的相似性和类别，特征空间中两个样本(点)之间的距离就是两个样本相似性的一种反映。常见的分类和聚类算法，如K近邻、K均值(K-means)、层次聚类等等都会选择一种距离或相似性的度量方法。根据数据特性的不同，可以采用不同的度量方法。一般而言，定义一个函数 \(dist(x,y)\), 若它是一个“距离度量”(distance measure)，则需要满足一些基本性质：

1. 非负性：\(dist(x_i,x_j)\ge0\);
2. 同一性：\(dist(x_i,x_j)=0\)当且仅当\(x_i=x_j\);
3. 对称性：\(dist(x_i,x_j)=dist(x_j,x_i)\)
4. 直递性：\(dist(x_i,x_j)\le dist(x_i,x_k)+dist(x_k,x_j)\).

注：直递性常被称为“三角不等式”

机器学习中的常见距离公式

1. 闵可夫斯基距离(Minkowski distance)

闵可夫斯基距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。

给定样本\(\pmb x_i=(x_{i1};x_{i2};\dots;x_{in})\)与\(\pmb x_j=(x_{j1};x_{j2};\dots;x_{jn})\)，\(\pmb x \in R^n\)是\(n\)维向量。

则闵可夫斯基距离可定义为：

\[dist(x_i,x_j)=\big(\sum_{u=1}^n|x_{iu}-x_{ju}|^p\big)^\frac{1}{p} \tag{1.1} \]

注：上式即为\(\pmb x_i - \pmb x_j\)的\(L_p\)范数\(||\pmb x_i - \pmb x_j||_p\)

对\(p\ge1\)，公式（1.1）显然满足距离度量的基本性质.

当\(p=2\)时，闵可夫斯基距离即欧氏距离(Euclidean distance) ：

\[dist(x_i,x_j)=||\pmb x_i - \pmb x_j||_2=\big(\sum_{u=1}^n|x_{iu}-x_{ju}|^2\big)^\frac{1}{2} \tag{1.2} \]

当\(p=1\)时，闵可夫斯基距离即曼哈顿距离(Manhattan distance)，亦称“街区距离”(city block distance)：

\[dist(x_i,x_j)=||\pmb x_i - \pmb x_j||_1=\sum_{u=1}^n|x_{iu}-x_{ju}| \tag{1.3} \]

当\(p\rightarrow \infty\)时，闵可夫斯基距离即切比雪夫距离(Chebyshev distance):

\[dist(x_i,x_j)=max_{u=1}^n|x_{iu}-x_{ju}| \]

无图无真相!!!

如图1所示，假设乘车从\(\pmb{x}_i\)点到\(\pmb{x}_j\)点（左下角和右上角两个黑色的点），图中灰色表示街道，白色方框表示建筑物。则绿色的斜线表示欧式距离。其他三条折线表示了曼哈顿距离，显然这三条折线的长度是相等的。

图1 欧氏距离与曼哈顿距离

从计算公式可以知道，坐标平面上到原点的欧氏距离(\(p=2\))相等的所有点组成的形状是一个圆，比如距离为1，则为一个半径为1的圆。类似的当\(p=1\)时，形状为菱形，\(p\)趋于\(\infty\)时，形状是正方形，如图2：

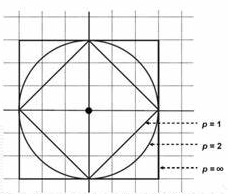
图2 p取值与距离

那么，当\(p\)取其他数值的时候呢？它是下面（图3）这样子哒：

图3 p的其他取值

注意，当\(p \lt 1\)时，闵可夫斯基距离不再满足直递性（即三角不等式），举个简单的反例：假设点\(\pmb{x}_i=(0,0)\)，\(\pmb{x}_j=(1,1)\)，和另一点\(\pmb{x}_u=(0,1)\)，当\(p\lt 1\)时，带入公式（1.1）计算\(\pmb{x}_i=(0,0)\)到\(\pmb{x}_j=(1,1)\)的距离等于\((1+1)^{1/p} \gt 2\), 而\(\pmb{x}_u=(0,1)\)到这两个点的距离都是1。

闵可夫斯基距离比较直观，但是它与数据的分布无关，具有一定的局限性，如果数据某一维度的值远远大于另一个维度的值，这个距离公式就会过度放大幅值较大维度的作用。所以，在实际应用计算距离之前，我们通常需要对数据进行标准化。

参考来源：
1）https://www.cnblogs.com/daniel-D/p/3244718.html
2）机器学习 - 周志华