机器学习笔记--模型的方差与偏差

什么是模型的方差和偏差

我们经常用过拟合、欠拟合来定性地描述模型是否很好地解决了特定的问题。从定量的角度来说，可以用模型的偏差（Bias）与方差（Variance）来描述模型的性能。在有监督学习中，模型的期望泛化误差可以分解成三个基本量的和---偏差、方差和噪声。

偏差、方差和噪声

1）使用文字描述的方式

我们知道，模型在不同训练集上学得的结果很可能不同，即便这些训练集是来自同一个分布。

偏差：指的是由所有采样得到的大小为\(m\)的训练数据集训练出的所有模型的输出的平均值和真实结果之间的差异，度量了模型的期望预测与真实结果的偏离程度，即刻画了模型本身的拟合能力。偏差通常是由于我们对模型做了错误的假设所导致的，比如真实模型是某个二次函数，但我们假设模型是一次函数。由偏差带来的误差通常在训练误差上就能体现出来。

方差：指的是由所有采样得到的大小为\(m\)的训练数据集训练出的所有模型的输出的方差，度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动对模型所造成的影响。方差通常是由于模型的复杂度相对于训练样本数\(m\)过高导致的，比如一共有100个训练样本，而我们假设模型是阶数不大于 200的多项式函数。由方差带来的误差通常体现在测试误差相对于训练误差的增量上，换句话说就是体现为训练误差可能很小，但是测试误差却很大。

噪声：则表达了在当前任务上任何模型所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度。

上述内容说明，模型的泛化性能是由模型本身的拟合能力、数据的充分性以及学习任务本身的难度所共同决定的。给定学习任务，为了取得好的泛化性能，则需使偏差较小，即能够充分拟合数据，并且使方差较小，即使得数据扰动产生的影响小。

2）使用数学公式描述的方式

模型的期望泛化误差可以分解成三个基本量的和---偏差、方差和噪声，即：

\[E(f; D) = bias^2(x) + var(x) + \epsilon^2 \]

注：《机器学习》-周志华，有上面公式的推导过程

此时，对于测试样本\(\pmb{x}\)，令\(y_D\)为\(\pmb{x}\)在数据集中的标记，\(y\)为\(\pmb{x}\)的真实标记，\(f(\pmb{x}; D)\)为训练集\(D\)上学得模型\(f\)在\(\pmb{x}\)上的预测输出。

以回归任务为例，模型的期望预测为：\(\overline{f}(\pmb{x})=E_D[f(\pmb{x};D)]\)

使用样本数相同的不同训练集产生的方差为：\(var(\pmb{x})=E_D[(f(\pmb{x};D)-\overline{f}(\pmb{x}))^2]\)

期望输出与真实标记的差别称为偏差 (bias)为：\(bias^2(\pmb{x})=(\overline{f}(\pmb{x})-y)^2\)

噪声为：\(\epsilon=E_D[(y_D-y)^2]\)

3）无图无真相

上面的定义可能不够直观，为了更清晰的理解偏差和方差， 我们用一个各种地方经常看到的射击的例子，对照上边的描述可以更好的理解这二者的区别和联系。假设一次射击就是一个机器学习模型对一个样本进行预测。射中靶心位置代表预测准确，偏离靶心越远代表预测误差越大。我们通过\(n\)次采样得到\(n\)个大小为\(m\)的训练样本集合，训练出\(n\)个模型，对同一个样本做预测，相当于我们做了\(n\)次射击，射击结果如图1所示。我们最期望的结果就是左上图的结果，射击结果又准确又集中，说明模型的偏差和方差都很小；右上图虽然射击结果的中心在靶心周围，但分布比较分散，说明模型的偏差较小但方差较大；同理，左下图说明模型方差较小，偏差较大；右下图说明模型方差较大，偏差也较大。

图1 方差和偏差

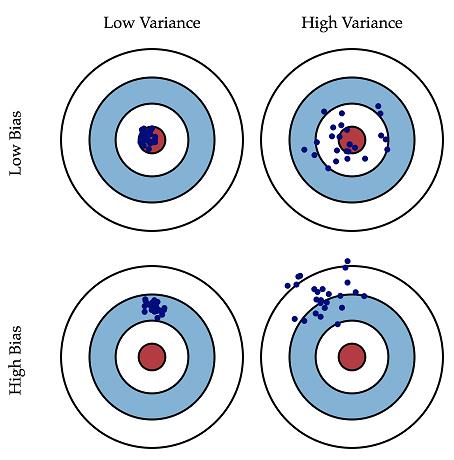
一般来说，偏差和方差是有冲突的，正如上面的公式所述，偏差、方差和期望泛化误差之间的关系是偏差一方差的权衡 (bias-variance trade-off) 。如果一个学习模型被称为测试性能好，那么要求该模型有较小的方差和较小的偏差。这就会涉及权衡的问题，因为直觉上我们会选择有极小偏差但可能是很大方差的方法(例如，画一条通过所有训练观测值的曲线)或追求小方差却大偏差的方法(对数据拟合一条水平线) 。在现实问题中，\(f\)一般是未知的，对一个学习模型来说是不可能精确地计算期望泛化误差、偏差及方差。然而，需要始终铭记偏差和方差的权衡。挑战在于如何找到一个方法使方差和偏差同时很小。至于使用什么方法，未完待续^_......

参考来源：
1）机器学习 - 周志华
2）统计学习导论-基于R应用
3）百面机器学习：算法工程师带你去