第4章 数据预处理
目录
4.1 数据清洗
4.1.1 缺失值处理
4.1.2 异常值处理
4.2 数据集成
4.2.1 实体识别
4.2.2 冗余属性识别
4.3 数据变换
4.3.1 简单函数变换
4.3.2 规范化
4.3.3 连续属性离散化
4.3.4 属性构造
4.3.5 小波变换
4.4 数据规约
4..4.1 属性规约
4.4.2 数值规约
4.1 数据清洗
主要是删除原始数据集中的无关数据、重复数据,平滑噪声数据,筛选掉与挖掘主题无关的数据,处理缺失值、异常值等。
4.1.1 缺失值处理
处理缺失值的方法分为3类:删除记录、数据插补和不处理。
1、常用的数据插补方法
| 均值/中位数/众数插补 | 根据属性值的类型,用该属性取值的均值/中位数/众数进行插补 |
| 使用固定值插补 | 将缺失的属性值用一个常量替换 |
| 最近临插补 | 在记录中找到与缺失样本数据最接近的样本的该属性值插补 |
| 回归方法 | 对带有缺失值的变量,根据已有数据和与其有关的其他变量(因变量)的数据建立拟合模型来预测缺失的属性值 |
| 插值法 | 利用已知点建立合适的插值函数f(x),未知值由对应点 xi 求出的函数值f ( xi )近似代替 |
插值方法:拉格朗日插值法、牛顿插值法、Hermite插值、分段插值、样条插值法等。
拉格朗日插值法利用Python实现:
import pandas as pd from scipy.interpolate import lagrange data=pd.read_excel(r'E:\siren\Python dataAnalyst\chapter4\demo\data\catering_sale.xls') # 过滤异常值,将其变为空值 data['销量'][(data['销量']<400)|(data['销量']>5000)]=None #自定义列向量插值函数 def ployinterp_column(s,n,k=5): y=s[list(range(n-k,n))+list(range(n+1,n+1+k))] #取数 y=y[y.notnull()] #剔除空值 return lagrange(y.index,list(y))(n) #插值并返回插值结果 #逐个元素判断是否需要插值 for i in data.columns: for j in range(len(data)): if (data[i].isnull())[j]: #如果为空即插值 data[i][j]=ployinterp_column(data[i],j)
4.1.2 异常值处理
在数据预处理时,异常值是否剔除,要视具体情况而定。
异常值处理常用方法
| 异常值处理方法 | 方法描述 |
| 删除含有异常值的记录 | 直接将含有异常值的记录删除 |
| 视为缺失值 | 将异常值视为缺失值,利用缺失值处理的方法进行处理 |
| 平均值修正 | 可用前后两个观测值的平均值修正改异常值 |
| 不处理 | 直接在具有异常值的数据集上进行挖掘 |
在很多情况下,要先分析异常值出现的可能原因,在判断异常值是否应该舍弃,如果是正确数据,可直接在具有异常值的数据集上进行挖掘建模。
4.2 数据集成
数据集成就是将多个数据源合并存放在一个一直的数据存储(如数据仓库)中的过程。
在数据集成时,来自多个数据源的现实世界实体的表达形式是不一样的,有可能不匹配,要考虑实体识别问题和属性冗余问题,从而将源数据在最底层上加以转换、提炼和集成。
4.2.1 实体识别
实体识别是指从不同数据源识别出现实世界的实体,它的任务是统一不同源数据的矛盾之处,常见形式:
(1)同名异义
数据源A中的属性ID和数据源B中的ID分别描述的是菜品编号和订单编号,即描述不同的实体。
(2)异名同义
数据源A中的sales_dt和数据源B中的sales_date都是描述销售日期的,即A.sales_dt=B.sales_date
(3)单位不统一
描述同一个实体分别用的是国际单位和中国传统的计量单位。
检测和解决这些冲突就是实体识别的任务。
4.2.2 冗余属性识别
数据集成往往导致数据冗余,例如:
(1)同一属性多次出现
(2)同一属性命名不一致导致重复
对于冗余属性要先分析,检测到后再将其删除。有些冗余属性可以用相关分析检测。
4.3 数据变换
数据变换主要是对数据进行规范化处理,将数据转换成“适当的”形式,以适用挖掘任务及算法的需要。
4.3.1 简单函数变换
简单函数变换是对原始数据进行某些数学变换,常用的变换包括平方、开方、取对数、差分运算等,即:
简单的函数变换常用来将不具有正态分布的数据变换成具有正态分布的数据。

4.3.2 规范化
数据规范化(归一化)处理是数据挖掘的一项基础工作。不同评价指标往往具有不同的量纲,数值间的差别可能很大,不进行处理可能会影响到数据分析的结果。为了消除指标间的量纲和取值范围差异的影响,进行标准化处理,将数据按照比例进行缩放,是指落到一个特定区域,便于进行综合分析。
(1)最小-最大规范化
也称离差标准化,是对原始数据的线性变换,将数值映射到[0,1]之间。
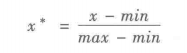
离差标准化保留了原来数据中存在的关系,是消除量纲和数据取值范围影响的最简单方法。
缺点:若数值集中且某个数值很大,则规范化后各值会接近于0,并且会相差不大。若将来遇到超过目前属性取值范围的时候,会引起系统错误,需要重新确定min和 max。
(2)零-均值规范化
也称标准差标准化,经过处理的数据的均值为0,标准差为1。是当前用得最多的数据标准化方法。
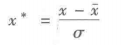
(3)小数定标规范化
通过移动属性值的小数位数,将属性值映射到[-1,1]之间,移动的小数位数取决于属性值绝对值的最大值。
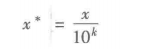
1 1 data=pd.read_excel(r'E:\siren\Python dataAnalyst\chapter4\demo\data\normalization_data.xls') 2 2 #标准差标准化 3 3 (data-data.mean())/data.std() 4 4 5 5 #最小-最大规范化 6 6 (data-data.min())/(data.max()-data.min()) 7 7 8 8 #小数定标规范化 9 9 data/10**np.ceil(np.log10(data.abs().max())
4.3.3 连续属性离散化
将连续属性变换成分类属性,即连续属性离散化。
1、离散化过程
连续属性的离散化就是在数据的取值范围内设定若干个离散的划分点,将取值范围划分为一些离散化的区间,最后用不同的符号或整数值代表落在每个子区间中的数据值。
离散化涉及2个子任务:1)确定分类数
2)如何将连续属性值映射到这些分类值。
2、常用的离散化方法
(1)等宽法
将属性的值阈分成具有相同宽度的区间,区间个数由数据本身的特点决定。
缺点:对离群点敏感,倾向于不均匀地把属性值分布到各个区间。有些区间包含许多数据,另外一些区间的数据很少,这样会损坏建立的决策模型。
(2)等频法
将相同数量的记录放进每个区间。
缺点:虽然避免了使用等宽法的问题,却可能将相同的数据值分到不同的区间以满足每个区间中固定的数据个数。
(3)基于聚类分析的方法
一维聚类的方法包括两个步骤:
1)将连续属性的值用聚类算法(如K-Means)进行聚类
2)将聚类得到的簇进行处理,合并到一个簇的连续属性值并做同一标记。
聚类分析的离散化方法也需要用户指定簇的个数,从而决定产生的区间数。
1 import pandas as pd 2 3 data = pd.read_excel(r'E:\siren\Python dataAnalyst\chapter4\demo\data\discretization_data.xls') #读取数据 4 data = data[u'肝气郁结证型系数'].copy() 5 k = 4 6 7 d1 = pd.cut(data, k, labels = range(k)) #等宽离散化,各个类比依次命名为0,1,2,3 8 9 #等频率离散化 10 w = [1.0*i/k for i in range(k+1)] 11 w = data.describe(percentiles = w)[4:4+k+1] #使用describe函数自动计算分位数 12 w[0] = w[0]*(1-1e-10) 13 d2 = pd.cut(data, w, labels = range(k)) 14 15 from sklearn.cluster import KMeans #引入KMeans 16 kmodel = KMeans(n_clusters = k, n_jobs = 4) #建立模型,n_jobs是并行数,一般等于CPU数较好 17 kmodel.fit(data.reshape((len(data), 1))) #训练模型 18 c = pd.DataFrame(kmodel.cluster_centers_).sort(0) #输出聚类中心,并且排序(默认是随机序的) 19 w = pd.rolling_mean(c, 2).iloc[1:] #相邻两项求中点,作为边界点 20 w = [0] + list(w[0]) + [data.max()] #把首末边界点加上 21 d3 = pd.cut(data, w, labels = range(k)) 22 23 def cluster_plot(d, k): #自定义作图函数来显示聚类结果 24 import matplotlib.pyplot as plt 25 plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签 26 plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号 27 28 plt.figure(figsize = (8, 3)) 29 for j in range(0, k): 30 plt.plot(data[d==j], [j for i in d[d==j]], 'o') 31 32 plt.ylim(-0.5, k-0.5) 33 return plt 34 35 cluster_plot(d1, k).show() 36 37 cluster_plot(d2, k).show() 38 cluster_plot(d3, k).show()
4.3.4 属性构造
利用已有的属性构造出新的属性,并加入到现有的属性集合中。
比如,进行防窃露电诊断建模时,已有的属性包括供入电量、供出电量。理论上供入电量=供出电量,但是传输过程中存在电能损耗,使得供入电量>供出电量,如果这条线路上的一个或多个大用户存在窃漏电行为,会使得供入电量明显大于供出电量。
为判断是否有大用户存在窃漏电行为,构造新指标-线损率,该过程就是构造属性。

线损率正常为3%~15%,如果远远超过这个范围,就可以认为该条线路的大用户可能存在窃漏电等用电异常行为。
4.4 数据规约
4.4.1 属性规约
通过属性合并来创建新属性维数,或者直接通过删除不相关的属性(维)来减少数据维数,从而提高数据挖掘的效率、降低计算成本。
目标:寻找出最小的属性子集并确保新数据子集的概率分布尽可能接近原来数据集的概率分布。
属性规约的常用方法:
(1)合并属性
(2)逐步向前选择
(3)逐步向后删除
(4)决策树归纳
(5)主成分分析
逐步向前选择、逐步向后删除、决策树归纳属于直接删除不相关属性方法。
4.4.2 数值规约
数值规约是指通过选择替代的、较小的数据来减少数据量,包括有参数方法和无参数方法两类。
有参数方法:使用一个模型来评估数据,只存放参数,而不是存放实际数据,如:回归和对数线性模型。
无参数方法:需要存放实际数据,如:直方图、聚类、抽样(采样)。
(1)直方图
(2)聚类
聚类技术奖数据元组(即记录,数据表中的一行)视为对象。将对象划分为簇,使一个簇中的对象相互“相似”,与其他簇中的对象“相异”。
(3)抽样
简单随机抽样
聚类抽样
分层抽样
(4)参数回归




 浙公网安备 33010602011771号
浙公网安备 33010602011771号