【带着canvas去流浪】（2）绘制折线图

我的github主页：https://github.com/dashnowords

我的新书上架啦，3天即登京东计算机编程语言类排行榜Top1！！！精选30+JavaScript库，从使用方式，设计原则，原理源码，周边知识等等多维度详细讲解，带你玩转前端花花世界，欢迎选购~

示例代码托管在：https://github.com/dashnowords/blogs/tree/master/Demo/canvas-echarts/line-chart

博客园地址：《大史住在大前端》原创博文目录

华为云社区地址：【你要的前端打怪升级指南】

目录

• 一. 任务说明
• 二. 重点提示
• 三. 示例代码
  • 3.1 一般折线图
  • 3.2 用贝塞尔曲线绘制平滑折线图
• 四. 大数据量场景

一. 任务说明

使用原生canvasAPI绘制折线图。（柱状图截图来自于百度Echarts官方示例库【查看示例链接】。

二. 重点提示

一般折线图是比较好实现的，只需要调用最基本的moveTo()和lineTo( )方法来绘制即可。平滑折线图是一个难点，需要借助贝塞尔曲线来进行绘制，此时每段曲线的控制点算法就成了核心难点，对原理感兴趣的读者可以自行研究，本文直接利用算法的结论来进行实现。

上一节中为了以文字中点为参考，在绘制x轴文字时采用的方法是用measureText( )方法测量文字的宽度，然后偏移该距离的一半来达到效果，事实上我们可以通过设置textAlign属性为'center'来达到以文字宽度方向中线为参考点的绘制。

context.textAlign = 'center';
context.drawText('Hello world',x ,y);

三. 示例代码

坐标轴及绘图参数设置请直接参见【带着canvas去流浪】（1）绘制柱状图或在示例demo中查看。

3.1 一般折线图

折线图数据绘制示例代码：

/**
 * 绘制数据
 */
function drawData(options) {
    let data = options.data;//数据点坐标
    let xLength = (options.chartZone[2] - options.chartZone[0])*0.96;//线段尾部留白后x轴长
    let yLength = (options.chartZone[3] - options.chartZone[1])*0.98;//线段尾部留白后y轴长
    let gap = xLength / options.xAxisLabel.length;//x轴间隙
    //缓存从数据值到坐标距离的比例因子
    let yFactor =(options.chartZone[3] - options.chartZone[1]) *0.98  /  options.yMax 
    let activeX =  0;//记录绘制过程中当前点的坐标
    let activeY =  0;//记录绘制过程中当前点的y坐标
    context.strokeStyle = options.barStyle.color || '#1abc9c'; //02BAD4
    context.strokeWidth = 2;
    context.beginPath();
    context.moveTo(options.chartZone[0],options.chartZone[3]);//先将起点移动至0,0坐标
    for(let i = 0; i < data.length; i++){
        activeX = options.chartZone[0] + (i + 1) * gap;
        activeY = options.chartZone[3] - data[i] * yFactor;
        context.lineTo(activeX, activeY);
     }
     context.stroke();
    }

浏览器中可查看效果：

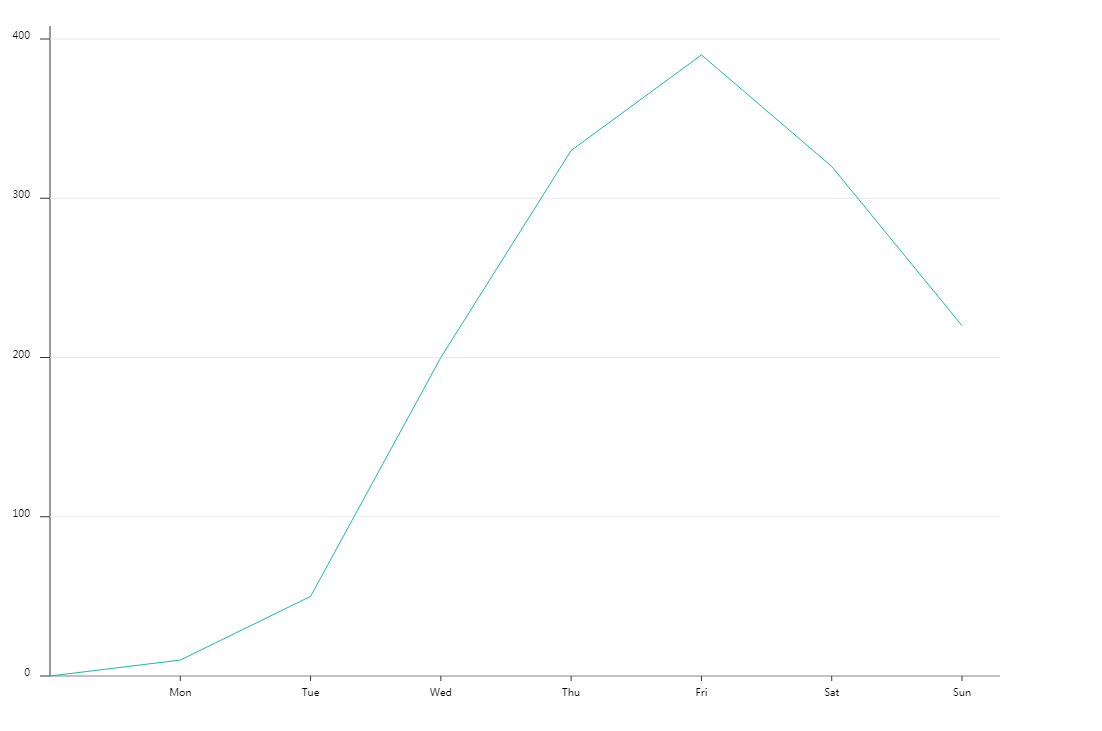
3.2 用贝塞尔曲线绘制平滑折线图

一般折线图连接点部分非常生硬，更多的场景下我们更希望曲线相对平滑，这时候就需要用到贝塞尔曲线来进行绘制，关于控制点的确定可参考文章【怎样确定贝塞尔曲线的控制点】。

👉关于Canvas图形绘制中坐标系的一点提示

为了将参数集中，options对象中记录的数据坐标是相对于我们自己绘制的坐标系的，为了使用canvas绘图上下文中的贝塞尔曲线绘制函数，需要在绘制时将数据点的坐标值转换为相对于canvas的坐标值。

本文示例中采用的基本算法为（为复现绘制过程，直接采用面向过程的编程方式）：

1. 绘制x轴文字时记录相对于可视坐标系的坐标值，并存储于options.xAxisPos数组中。
2. 由于数据点是对齐x轴文字来绘制的，所以options.xAxisPos及options.data中存储的坐标对就是数据点在可视坐标中的坐标点。
3. 遍历数据坐标点，计算使用三次贝塞尔曲线连接相邻点时的控制点的坐标，此时控制点坐标是相对于可视坐标系的，再经过坐标变换函数transToCanvasCoord( )处理将坐标数值转换为相对于canvas坐标系的数值。
4. 使用context.bezierCurveTo(c1x, c1y, c2x, c2y, dx dy)函数来绘制拟合曲线。

示例代码为：

/**
 * 三次贝塞尔曲线数据拟合
 */
function drawDataWithCubicBezier(options) {
    //计算用于绘图的数据点和控制点坐标
    let drawingPoints = calcControlPoints(options);
    //设置绘图样式
    context.strokeStyle = options.barStyle.color || '#1abc9c'; //02BAD4
    context.strokeWidth = 4;
    context.beginPath();
    context.moveTo(options.chartZone[0],options.chartZone[3]);//先将起点移动至0,0坐标
    //逐个连接相邻坐标点
    for(let i = 1; i < drawingPoints.length; i++){
       context.bezierCurveTo(drawingPoints[i-1].cp1x, drawingPoints[i-1].cp1y, drawingPoints[i-1].cp2x, drawingPoints[i-1].cp2y, drawingPoints[i].dx, drawingPoints[i].dy);
    }
    //绘制线条
    context.stroke();
}

/**
 * 计算控制点
 * 本例采用的算法，在每个点计算时需要用到该点左侧1个点和右侧2个点的坐标信息，影响边界点的绘制，本例中采用的方法为直接复制边界点坐标来简化边界点的坐标求值。
 */
function calcControlPoints(options) {
    let results = [];
    let y = options.data;
    let x = options.xAxisPos;
    //补充左值
    y.unshift(y[0]);
    x.unshift(0);
    //补充右值
    x.push(x[y.length - 1]);
    x.push(x[y.length - 1]);
    y.push(y[y.length - 1]);
    y.push(y[y.length - 1]);
    //计算用于绘制曲线的坐标点及控制点坐标值
    for(let i = 1; i < y.length - 2; i++){
        results.push({
            dx:transToCanvasCoord(x[i], 'x'),
            dy:transToCanvasCoord(y[i]),
            cp1x:transToCanvasCoord(x[i] + (x[i+1] - x[i-1]) / 4,'x'),
            cp1y:transToCanvasCoord(y[i] + (y[i+1] - y[i-1]) / 4),
            cp2x:transToCanvasCoord(x[i+1] - (x[i+2] - x[i]) / 4,'x'),
            cp2y:transToCanvasCoord(y[i+1] - (y[i+2] - y[i]) / 4),
        })
    }
    console.log(results)
    return results;
}

/**
 * 将坐标转换为相对canvas的坐标
 * @param  {[type]} coord 相对于可视坐标系的值
 * @param  {[type]} flag  标记转换x坐标还是y坐标
 */
function transToCanvasCoord(coord,flag) {
    let xLength = (options.chartZone[2] - options.chartZone[0])*0.96;
    let yLength = (options.chartZone[3] - options.chartZone[1])*0.98;
    let yFactor =(options.chartZone[3] - options.chartZone[1]) *0.98  /  options.yMax;
    if (flag === 'x') {
        return coord + options.chartZone[0];
    }
    return options.chartZone[3] - coord * yFactor;
}

👉Tips：

1. 在实际开发中，反复出现的计算结果可以通过闭包的形式缓存下来，例如本例中transToCanvasCoord( )函数中前半部分的计算实际上每次进行坐标转换时都会计算，这是没必要的。
2. 上例中的算法在计算控制点时是以当前点x[i]计算连接x[i]到x[i|+1]时的控制点坐标并进行保存，而绘图时当循环变量为i时，drawingPoints[i]中存储的控制点坐标，是连接至(x[ i+1 ],y[ i+1 ])时的控制点，所以取用参数时需要错一位。当然也可以在计算drawingPoints时直接按需存储即可。

在浏览器中可以看到曲线拟合的绘制效果:

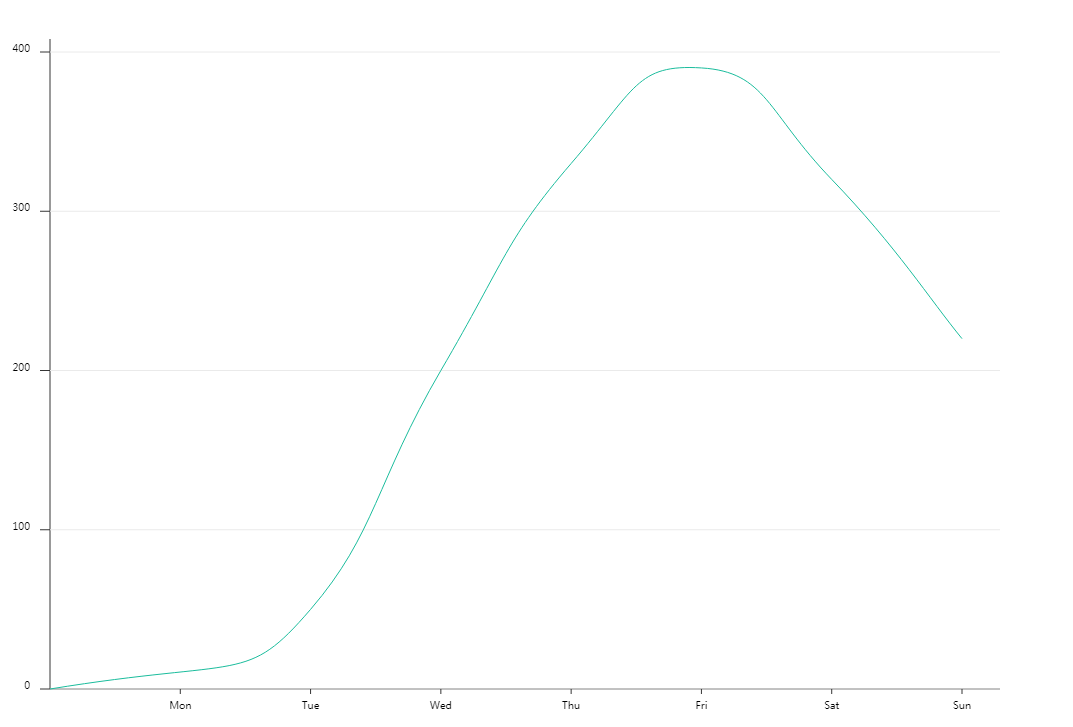
四. 大数据量场景

面对大数据量的可视化展现或是在交互后出现重绘时，就极容易造成主线程阻塞，这是需要极力避免的。常见的处理思路有以下几种：

1. 数据采样并重新拟合以减少绘图数据点，也就是从源数据到绘图数据进行映射，毕竟显示器分辨率就那么高，过大的数据量加重了数据损失，却并不一定能在视觉和效果上获得对应的提升。
2. 将大数据量及耗时的处理发送至webWorker中，利用工作线程来处理计算密集型任务。
3. 将同步的绘图任务分解为若干个异步的子任务来执行，避免阻塞主线程。

笔者阅历有限，并没有生产环境的大数据量绘制的性能优化实战经验，能想到的就是上面几点，非常欢迎有相关经验的读者交流讨论。