野生前端的数据结构练习（11）动态规划算法

我的github主页：https://github.com/dashnowords

我的新书上架啦，3天即登京东计算机编程语言类排行榜Top1！！！精选30+JavaScript库，从使用方式，设计原则，原理源码，周边知识等等多维度详细讲解，带你玩转前端花花世界，欢迎选购~

一.动态规划算法

dynamic programming被认为是一种与递归相反的技术，递归是从顶部开始分解，通过解决掉所有分解出的问题来解决整个问题，而动态规划是从问题底部开始，解决了小问题后合并为整体的解决方案，从而解决掉整个问题。

动态规划在实现上基本遵循如下思路，根据边界条件得到规模较小时的解，小规模问题合并时依据递推关系式进行，也就是说较大规模的问题解可以由较小问题的解合并计算得到。最经典易懂的就是使用递归算法和动态规划算法两种不同的方式来计算斐波那契数列或求阶乘的对比，动态规划算法的特性相当于对计算过程进行了缓存，避免了不必要的重复计算。

本篇通过几个典型的相关实例来学习和练习动态规划算法。

二.寻找最长公共子串

题目不难理解，例如在单词“raven”和“havoc”的最长公共子串就是av。最容易想到的算法就是暴力求解，也称为贪心算法，在下一篇中会提供贪心算法暴力求解最长公共子串的示例代码。

算法描述如下：

字符串1长为m,字符串2长为n,先生成一个m*n的矩阵L并将其中都填充为0，矩阵中的值L[x,y]表示如果存在公共字符串，那么该字符串在字符串1中的位置为从x-L[x,y]到x，在字符串2中的位置为从y-L[x,y]到y，换句话说：L[x,y]记录了如果当前位置为公共子串的截止点时公共子串的长度。

递推关系式如下:

若str1[x] === str2[y], L[x,y] = L[x-1,y-1] + 1;

若str1[x] !== str2[y], L[x,y] = 0;

从图中可以更清晰地看到动态规划算法在寻找公共子串时的过程：

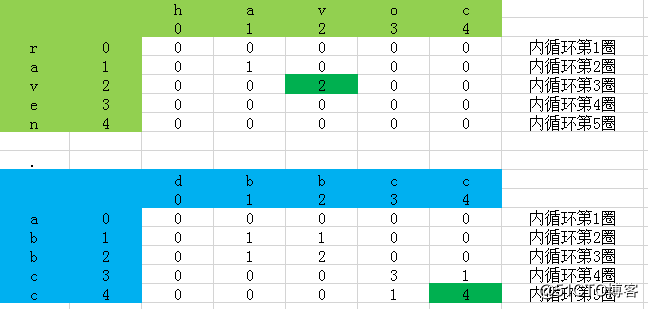
该表从左上角开始填空，循环遍历每个格子，如果str1中的字符和str2中的某个字符相同，则需要找到其左上角格子的数字，然后加1填在自己的格子里，如果不相等则填0，最终记录表中最大的值即为最长公共子串的结束位置，打印出最长公共子串也就很容易实现了。

参考代码：

/**
 * 动态规划求解最长公共子串
 */
function lcs(str1,str2) {
    let record = [];
    let max = 0;
    let pos = 0;
    let result = '';
    //初始化记录图
    for(let i = 0; i < str1.length; i++){
        record[i] = [];
        for(let j = 0; j < str2.length; j++){
            record[i][j] = 0;
        }
    }
    //动态规划遍历
    for(let i = 0; i < str1.length; i++){
        for(let j = 0; j < str2.length; j++){
            if (i === 0 || j === 0) {
                record[i][j] = 0;
            }else{
                if (str1[i] === str2[j]) {
                     record[i][j] = record[i-1][j-1] + 1;
                } else {
                     record[i][j] = 0;
                }
            }
            //更新最大值指针
            if (record[i][j] > max) {
                max = record[i][j];
                pos = [i];
            }
        }
    }
    //拼接结果
    if (!max) {
        return '';
    } else {
        for(let i = pos ; i > pos - max ; i--){
            result = str1[i] + result;
        }
        return result;
    }
}

console.log(lcs('havoc','raven'))
console.log(lcs('abbcc','dbbcc'))

三.0-1背包问题递归求解

0-1背包问题用递归或动态规划都可以求解，通过本例和下一节的例子就可以对比两种算法相反的求解过程。

背包问题是算法中一个经典的大类，从简单到复杂一本书都讲不完，本例中仅实现简单的0-1背包问题，这类问题是指被放入背包的物品只能选择放或者不放，不能只放入一部分。

0-1背包问题的描述是这样的，假设保险箱中有n个物品，他们的尺寸存放在size[ ]数组中，每一个的价值存放在values[ ]数组中，你现在拥有一个背包，其容量为capacity，问应该装哪些东西进背包，使得被装入的物品总价值最大。

算法描述和递推关系式如下:

1. 如果第n个物品无法放入背包，则最大价值等同于将其他物品放入背包时能得到的最大价值：

   maxValue = knapsack(capacity,size,values,n-1)

2. 如果第n个物品能够放入背包，则最大价值等同于下列两种情况中较大的一个：

   2.1 放入物品n,maxValue = knapsack(capacity - size[n], size, values, n-1)+values[n]

   2.2 不放物品n,maxValue = knapsack(capacity, size, values, n-1)

代码实现如下：

/**
 * 递归求解0-1背包问题
 * 算法：
 * 1.如果单个物品体积超出背包容量，则肯定不拿
 * 2.如果单个物品体积未超出背包容量，则问题变为在下列两种情况中取较大的值
 * 2.1 放入当前物品 knapsack(capacity - size[n-1], size, value, n-1) + value[n-1])
 * 2.2 不放入当前物品 knapsack(capacity, size, value, n-1) 
 */
function max(a,b) {
    return a>b?a:b;
}

/**
 * 
 * @param  {[type]} capacity 背包容量
 * @param  {[type]} size     物品体积数组
 * @param  {[type]} value    物品价值数组
 * @param  {[type]} n        物品个数
 * @return {[type]}          最大价值
 */
function knapsack(capacity, size, value, n) {
    //如果没有物品或者背包容量为0 则无法增值
    
    if (n == 0 || capacity == 0 ) {
        return 0;
    }
    if (size[n-1] > capacity) {
        //算法步骤1 从最后一个物品开始，如果单个物品超出容量限制则不放入
        return knapsack(capacity, size, value, n-1);
    } else {
        //算法步骤2
        return max(knapsack(capacity - size[n-1], size, value, n-1) + value[n-1],knapsack(capacity, size, value, n-1));
    }
}

let value = [4,5,10,11,13];
let size = [3,4,7,8,9];
let capacity = 16;
let n = 5;

let result = knapsack(capacity, size, value, n);
console.log('result:',result);

可以看到代码基本只是用程序语言实现了算法描述并进行了一些边界条件的处理，并没有进行任何实现方法上的优化，从它不断调用自身就可以看出这是一个很明显的递归方法。在递归方法下，由于重复访问计算的问题，很难打印出最终到底选择了哪些物品，而在下面的动态规划算法的解法中就相对容易实现。

四.0-1背包问题动态规划求解

动态规划算法来求解0-1背包问题，核心递推关系上并没有什么差异，但正如开头所讲，动态规划的优势就是对计算过的结果进行了缓存，所以采用这个算法进行0-1背包问题求解得到最终结果后，可以再自顶向下反向查询从缓存的表格中查出这个解的实现路径，从而就可以判断每个物品是否被选入当前解。

动态规划算法实现如下：

/**
 * 动态规划求解0-1背包问题
 */
function max(a,b) {
    return a>b?a:b;
}

/**
 * 
 * @param  {[type]} capacity 背包容量
 * @param  {[type]} size     物品体积数组
 * @param  {[type]} value    物品价值数组
 * @param  {[type]} n        物品个数
 * @return {[type]}          最大价值
 */
function knapsack(capacity, size, value, n) {
    //K[n][capacity]表示0~n-1这n个物品入选时的最优值
    let K = [];
    let pick = [];
    let result = 0;
    for (let i = 0; i <= n ; i++){
       K[i] = [];
       for(let j = 0; j <= capacity; j++){
          if(j === 0 || i === 0){
            //i=0为防御性编程，没有实际意义
            //j=0表示背包容量为0，无法放入故结果为0
            K[i][j] = 0;
          } else if (size[i-1] > j){
            //如果背包容量比第i个物品的重量还小，则第i个物品必然无法放入，相当于前i-1个物品放入j容量背包时的最值
            K[i][j] = K[i-1][j];
          } else {
            //动态规划解,当第i个物品可以放入时，K[i][j]等同于放入i时最值和不放i时的值取最大
            K[i][j] = max(K[i-1][j-size[i-1]] + value[i-1], K[i-1][j]);
          }
       }
    }
    result = K[n][capacity];
    
    //如何求解到底选了哪些物品?
    while(n > 0){
        if (K[n-1][capacity - size[n-1]] + value[n-1] > K[n-1][capacity]) {
            capacity -= size[n-1];
            n--;
            pick[n] = 1;
        } else {
            n--;
            pick[n] = 0;
        }
    }
    console.log('答案的选择情况为:',pick);
    return result;
}

let value = [4,5,10,11,13];
let size = [3,4,7,8,9];
let capacity = 16;
let n = 5;

let result = knapsack(capacity, size, value, n);
console.log('结果:',result);