Java数据结构与算法-树
(摘录加总结------)
一、树的概念
(1)树是一种非线性的数据结构,是由n(n>=1)个有限节点组成的有层次关系的集合,在树中有许多节点,每一个节点最多只有一个父节点,并且可能会有0个或者更多个子节点,没有父节点的那个称为根节点,除了根节点外,每个节点又可分为多个不相交的子树。

(2)树的相关概念术语:
1)节点<node>
树中每个元素都叫节点2)根节点或树根<root>
树顶端的节点称之为根节点,也叫树根3)子树<subTree>
除根节点之外,其他节点可以分为多个树的集合,叫做子树,在上图中,K这个节点可以称之为一颗子树,而H、K、L三个节点组合起来也可以叫做一颗子树4)节点的度
一个节点直接含有的子树的个数,称之为节点的度。比如上图中B节点的度为3,C节点的度是2,I、J、K、L节点的度是05)叶子节点、叶节点、终端节点
度为0的节点叫做叶子节点,也叫叶节点、终端节点,其实就是没有子节点的节点,或者说没有子树的节点6)双亲节点、父节点
父节点就是一个节点上头的那个节点,如果一个节点包含若干子节点,那么这个节点就是这些子节点的父节点,也叫双亲节点7)兄弟节点
拥有相同父节点的节点互称为兄弟节点8)树的度
一棵树中最大节点的度称之为树的度,即树中哪个节点的子节点最多,那么这个节点的度也就是树的度9)节点的层次
从根这一层开始,根算1层,根的子节点算2层,一直到最下面一层10)树的高度、深度(这里属于树的层次结构)
树的深度是从根节点开始、自顶向下逐层累加(根节点的高度是1)助记:深度从上到下
树的高度是从叶节点开始、自底向上逐层累加(叶节点的高度是1)助记:高度由下向上
虽然树的高度和深度一样,但是具体到某个节点上,其高度和深度通常是不一样的。 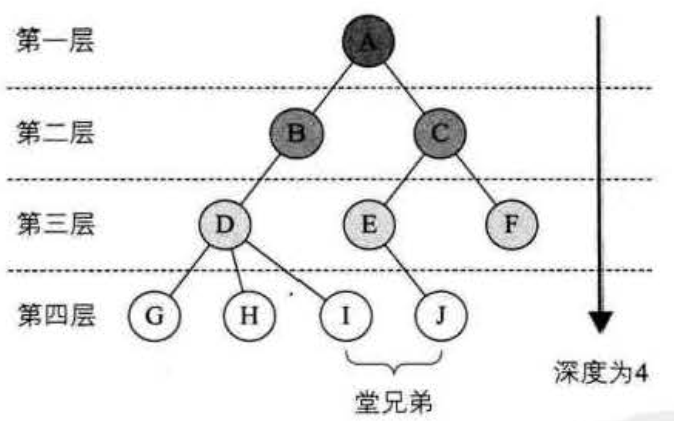
11)堂兄弟节点
堂兄弟节点是同一层,父节点不同,或者说双亲节点在同一层的节点称之为堂兄弟节点712)节点的祖先
从根节点到某一节点一路顺下来的除了该节点的所有节点都是该节点的祖先节点13)节点的子孙
以某节点为根的子树中,任何一个节点都是其子孙,也就是说这个节点下面与这个节点有关的节点都是这个节点的子孙14)森林
由m棵不相交的树组成的集合,叫做森林,对比树中每个节点的子树的集合其实就构成了森林。(3)常见的树的分类:
常接触到的树有:二叉树、平衡二叉树、二叉查找树、B树、B+树、B*树、哈夫曼树、红黑树、trie树等。
(4)树的存储结构的实现
public class TreeNode1{
private int data;
private int parent;
public int getData(){
return date;
}
public void setData(int data){
this.data = data;
}
public int getParent(){
return parent;
}
public void setParent(int parent){
this.parent = parent;
}
}
上面的这个实现是利用了双亲表示法,约定根节点的位置域为-1,这样的存储结构,我们可以根据结点的 parent 指针很容易找到它的双亲结点,所用的时间复杂度为 0(1) ,直到 parent 为-1 时,表示找到了树结点的根。可如果我们要知道结点的孩子是什么,对不起,请遍历整个结构才行。


另外我们可以使用孩子表示法的多重链表表示方法来表示,但是考虑到表示的准确性和资源浪费程度,考虑这样子表示的方法是比较可以的:
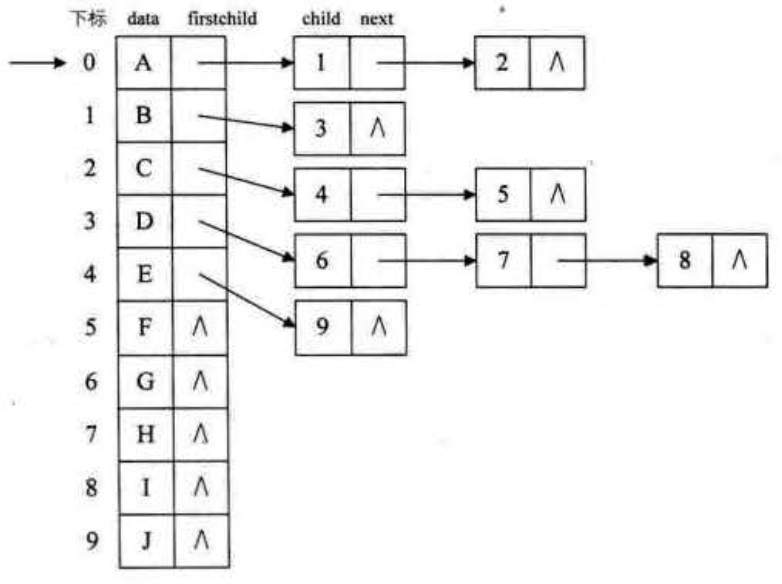
将一个树里面所有的节点按照顺序存储结构形式将其放入到一个数组里面,然后每一个节点对其子节点按照链表的形式进行拓展,即这个数组里面存储的节点的指针域是存储的该节点的孩子链表的头指针,如果有N个节点的话就应该有N个线性表,比如索引为3的D节点,它有3个子节点,所以以D这个头指针发散出来的表达了6,7,8即G,H,J的子节点之间的逻辑关系的链表表示如图所示,并且子节点为零的节点它的指针域就会为空。
这样的结构对于我们要查找某个结点的某个孩子,或者找某个结点的兄弟,只需要查找这个节点的孩子单链表即可,对于遍历整棵树也是很方便的。
若是对于这个结构进行进一步改进的话,将双亲关系表示进去:(双亲孩子表示法)
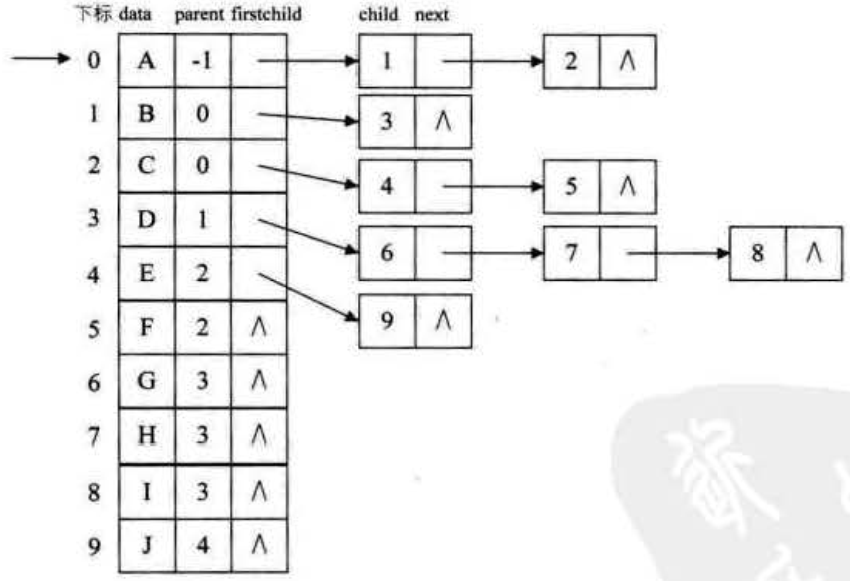
(孩子兄弟表示法):任意一棵树,它的节点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此我们设置两个指针,分别指向该节点的第一个孩子和此节点的右兄弟。但是如果是对于上图所示的树来看的话,对于节点D,它有三个子节点:G,H,I,其中H是G的右兄弟,I是G的右兄弟,同时对于I来说没有它的再对应的右兄弟了,所以它的两个指针域应该为空。
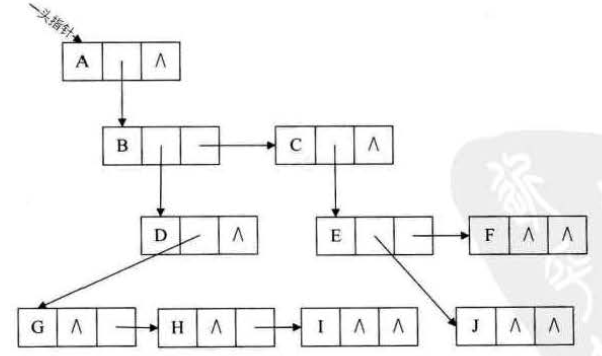
对于每一个节点类的编写就应该包含:data,firstChild,rightBro这三个属性。如果想要找到某个节点的双亲,可以考虑再在此基础上添加一个parent指针域来解决快速朝招双亲的问题。这个表示法的最大好处就是把一颗复杂的树变成了一棵二叉树。
二、二叉树
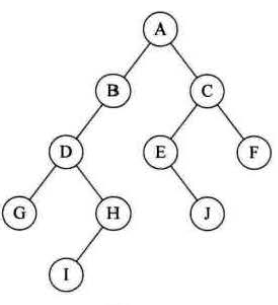
对于在某个阶段都是两种结果的情形,比如开和关、0和1、真和假、上和下、对与错、正面与反面,都适合用树状结构来建模,这种树是一种很特殊的树状结构,称之为二叉树。对于上图中的树由于D有三个节点,所以它不是二叉树。
(1)二叉树的特点:
二叉树中不存在子树或者有一棵子树都是可以的。左子树和右子树是有顺序的,次序不能任意颠倒。即使树中某节点只有一棵子树也要区分它是左子树还是右子树。由于要区分左子树和右子树比如三个节点的树:
有五种不同的形态:

(2)特殊的二叉树
斜树:线性表就是一种树的极其特殊的表现形式。比如上面的树2和树5。
满二叉树: 非叶子节点的度一定是2。
非叶子节点的度一定是2。
完全二叉树:满二叉树一定是完全二叉树,但是完全二叉树不一定是满二叉树。(按层次编号一一对应)相当于是满二叉树的某些位置去掉之后的树,形式上还是满足满二叉树的形式的。

(3)二叉树的性质(这些性质基本上都是归纳法出来的)
性质1:在二叉树的第i层上至多有2^(i-1)个节点(i>=1)。
性质2:深度为k的二叉树至多有2^k-1个节点(k>=1)。最多就是满二叉树的情况。
性质3:对任何一棵二叉树T,如果其终端节点数(叶子节点数)为n0,度为2的节点数为n2,则n0=n2+1。(除了叶子节点外只有度为1或2的节点数了)
性质4:具有n个节点的完全二叉树的深度为【log2n】+1(【x】表示不大于x的最大整数)。由于深度为k的满二叉树的节点数n一定是2^k-1,这个深度就是该二叉树的度,所以反推可以得到满二叉树的度k=log2(n+1)。
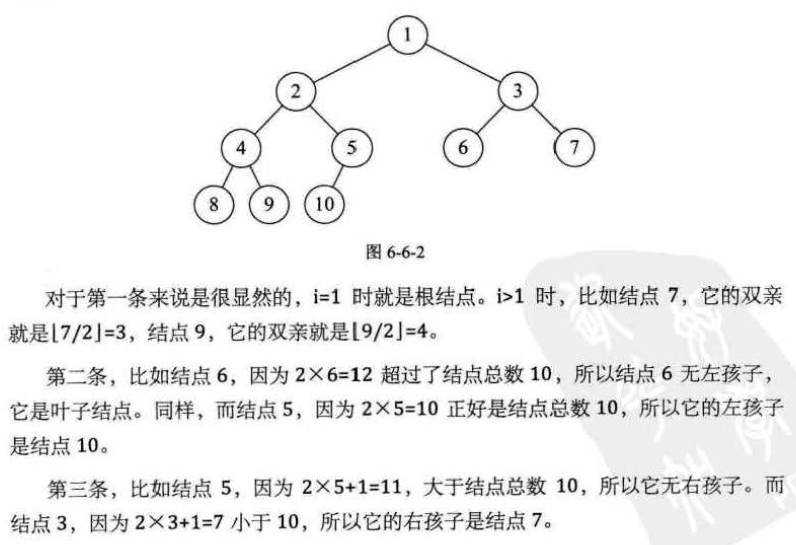
性质5:如果对一棵有n个节点的完全二叉树(其深度为【log2n】+1)的节点按层序编号(从第一层到第【log2n】+1层,每层从左到右),对任一节点i(1<=i<=n)有:

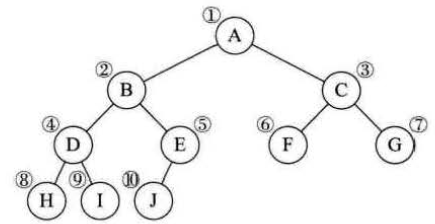
(4)二叉树顺序存储结构
二叉树的特殊性导致使用顺序存储结构也可以实现。使用一维数组存储二叉树中的节点,并且节点的存储位置也就是数组的下表要能体现节点之间的逻辑关系,比如双亲与孩子的关系,左右与兄弟的关系。

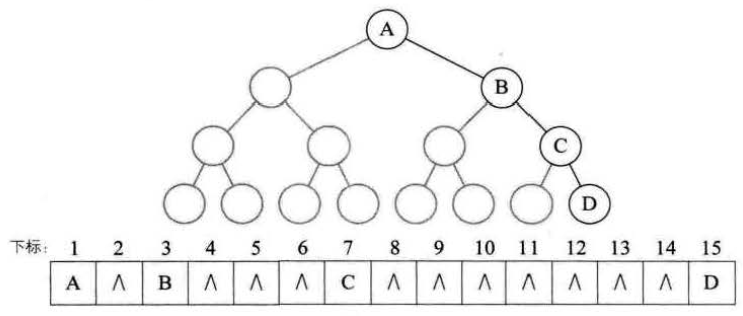
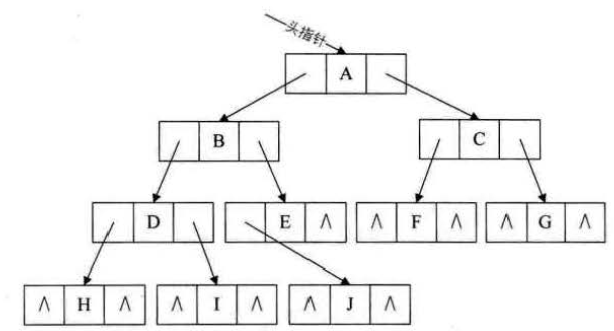
对于一般的树尽管层序编号不能反映逻辑关系,但是可以将其按完全二叉树编号,只不过把不存在的节点设置为^,但是可能会存在存储空间的浪费,所以一般只用于完全二叉树。
(5)二叉树连式存储结构
也称为二叉链表,为其设计一个数据域和两个指针域是比较自然的想法。二叉树的每个节点最多有两个孩子。
三、二叉树的遍历
二叉树的遍历:指从根节点出发,按照某种次序一次访问二叉树中所有的节点。使得每个节点被访问一次且仅被访问一次。这存在一个遍历次序的不确定性问题,因为树的节点之间不存在唯一的前驱和后继关系。
二叉树遍历方法:
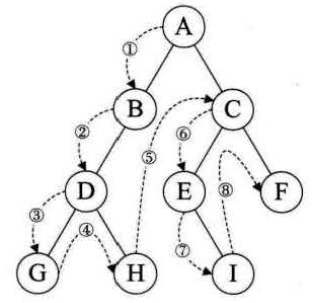
(1)前序遍历
若二叉树为空,则空操作返回,然后访问顺序是访问根节点,然后遍历左子树和右子树。
public void PreOrder(BinaryTreeNode node){
if(node!=null){
System.out.println(node.getData()); //先访问根节点
PreOrder(node.getLeftChirld()); //先根遍历左子树
PreOrder(node.getRightChirld()); //先根遍历右子树
}
}
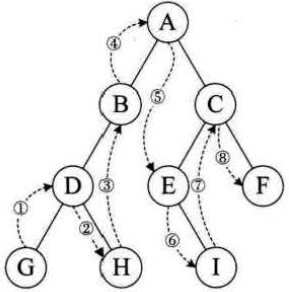
(2)中序遍历
若树为空,则空操作返回,遍历顺序从根节点开始但是不是先访问根节点,而是从左子树的终端节点开始,遍历左子树,然后访问根节点,再中序遍历右子树。
public void InOrder(BinaryTreeNode node){
if(node!=null){
InOrder(node.getLeftChirld()); //中根遍历左子树
System.out.println(node); //访问根节点
InOrder(node.getRightChirld()); //中根遍历右子树
}
}
(3)后序遍历
若树为空,则空操作返回,遍历顺序从左到右先叶子后节点的方式便利访问左右子树,最后是访问根节点。

public void PostOrder(BinaryTreeNode node){
if(node!=null){
PostOrder(node.getLeftChirld()); //后根遍历左子树
PostOrder(node.getRightChirld()); //后根遍历右子树
System.out.println(node); //访问根节点
}
}
}
(4)层序遍历
若树为空,则空操作返回,遍历顺序从树的第一层,从根节点开始访问,从上而下逐层遍历,在同一层中,按照从左到右的顺序对节点逐个访问。

这四种遍历方法都是在把树中的节点变成某种意义的现行序列。
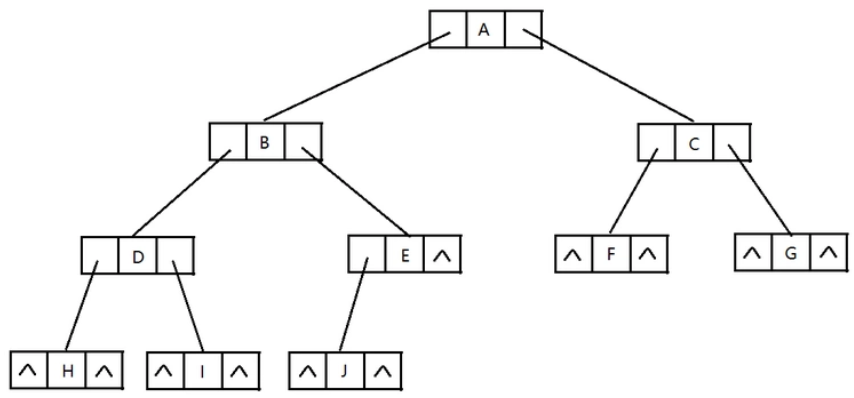
二叉树的创建:二叉树的左右子节点仍然是一棵二叉树。
(1)表示方法:左右链表表示法
public class BinaryTreeNode {
private int data; //数据
private BinaryTreeNode leftChirld; //左孩子
private BinaryTreeNode rightChirld; //右孩子
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public BinaryTreeNode getLeftChirld() {
return leftChirld;
}
public void setLeftChirld(BinaryTreeNode leftChirld) {
this.leftChirld = leftChirld;
}
public BinaryTreeNode getRightChirld() {
return rightChirld;
}
public void setRightChirld(BinaryTreeNode rightChirld) {
this.rightChirld = rightChirld;
}
}
(2)创建二叉树:操作二叉树,初始化根节点或者初始化一个空二叉树。
public class BinaryTree {
private BinaryTreeNode root;
//初始化二叉树
public BinaryTree(){}
public BinaryTree(BinaryTreeNode root){
this.root = root;
}
public void setRoot(BinaryTreeNode root){
this.root = root;
}
public BinaryTreeNode getRoot(){
return root;
}
}
(3)二叉树的清空:清空大致分为两步,首先清空某个节点为根节点的子树,递归地删除每个节点。接着再删除根节点。
/**
* 二叉树的清空:
* 首先提供一个清空以某个节点为根节点的子树的方法,既递归地删除每个节点;
* 接着提供一个删除树的方法,直接通过第一种方法删除到根节点即可
*/
//清除某个子树的所有节点
public void clear(BinaryTreeNode node){
if(node!=null){
clear(node.getLeftChirld());
clear(node.getRightChirld());
node = null; //删除节点
}
}
//清空树
public void clear(){
clear(root);
}
(4)判断树是否为空:只需判断根节点是否为空即可。
//判断二叉树是否为空
public boolean isEmpty(){
return root == null;
}
(5)求树的高度:思路,首先需要一种获取以某个节点为子树的高度方法,使用递归实现。如果一个节点为空,那么这个节点肯定是一颗空树,高度为0;如果不为空,则遍历地比较它的左右子树高度,高的一个为这颗子树的最大高度,然后加上自身的高度即可。
/**
* 求二叉树的高度:
* 首先要一种获取以某个节点为子树的高度的方法,使用递归调用。
* 如果一个节点为空,那么这个节点肯定是一颗空树,高度为0;
* 如果不为空,那么我们要遍历地比较它的左子树高度和右子树高度,
* 高的一个为这个子树的最大高度,然后加上自己本身的高度就是了
* 获取二叉树的高度,只需要调用第一种方法,即传入根节点
*/
//获取二叉树的高度
public int heigh(){
return heigh(root);
}
//获取以某节点为子树的高度
public int heigh(BinaryTreeNode node){
if(node==null){
return 0; //递归结束,空子树高度为0
}else{
//递归获取左子树高度
int l = heigh(node.getLeftChirld());
//递归获取右子树高度
int r = heigh(node.getRightChirld());
//高度应该算更高的一边,(+1是因为要算上自身这一层)
return l>r? (l+1):(r+1);
}
}
(6)求二叉树的节点数:思路,获取二叉树节点数,需要获取以某个节点为根的子树的节点数实现。
如果节点为空,则个数肯定为0;如果不为空,则算上这个节点之后,继续递归计算所有子树的节点数,全部相加即可
/**
* 获取二叉树的节点数
*/
public int size(){
return size(root);
}
/**
* 求二叉树的节点数:
* 求节点数时,我们看看获取某个节点为子树的节点数的实现。
* 首先节点为空,则个数肯定为0;
* 如果不为空,那就算上这个节点之后继续递归所有左右子树的子节点数,
* 全部相加就是以所给节点为根的子树的节点数
* 如果求二叉树的节点数,则输入根节点即可
*/
public int size(BinaryTreeNode node){
if(node==null){
return 0; //如果节点为空,则返回节点数为0
}else{
//计算本节点 所以要+1
//递归获取左子树节点数和右子树节点数,最终相加
return 1+size(node.getLeftChirld())+size(node.getRightChirld());
}
}
(7)返回某节点的父亲节点:思路,首先,同样需要通过一种方法来获取某个节点在某个子树中的父节点,这里使用递归实现,接着通过这种方法获取这个节点在二叉树中的父节点事实上,以现有的这种二叉树的形式,我们并没有办法直接获取一个节点的父节点, 这里只能通过从根节点遍历来比较获取。
//node节点在subTree子树中的父节点
public BinaryTreeNode getParent(BinaryTreeNode subTree,BinaryTreeNode node){
if(subTree==null){
return null; //如果是空子树,则没有父节点
}
if(subTree.getLeftChirld()==node || subTree.getRightChirld() == node){
return subTree; //如果子树的根节点的左右孩子之一是待查节点,则返回子树的根节点
}
BinaryTreeNode parent = null;
if(getParent(subTree.getLeftChirld(),node)!=null){
parent = getParent(subTree.getLeftChirld(),node);
return parent;
}else{
//递归左右子树
return getParent(subTree.getRightChirld(),node);
}
}
//查找node节点在二叉树中的父节点
public BinaryTreeNode getParent(BinaryTreeNode node){
return (root==null||root==node)? null:getParent(root,node);
}
(8)二叉树的插入:二叉树的插入分析:
* 分两种情况:插入某个节点的左子节点;插入某个节点的右子节点
* 值得指出的是,当这个节点本身有子节点时,这样的插入也会覆盖原来在这个位置上的节点。
* 另外,虽然插入的是子节点,但是子节点也可以代表一颗子树。
* 因为但从这个节点来看并不知道这个节点是否有左右子树存在,所以虽然插入的是一个节点,但有可能
* 插入可很多节点(插入的是一颗子树)
//给某个节点插入左节点
public void insertLeft(BinaryTreeNode parent,BinaryTreeNode newnode){
parent.setLeftChirld(newnode);
}
//给某个节点插入右节点
public void insertRitht(BinaryTreeNode parent,BinaryTreeNode newnode){
parent.setRightChirld(newnode);
}


