桶排序+基数排序+计数排序
桶排序
1.原理：
将需要排序的数组分在有限的桶里
然后对每个桶中的数分别排序
（对每个桶的操作：1.别的排序算法 2.以递归的方式继续使用桶排序）
2.过程：
- 假设待排序的一组数统一的分布在一个范围中，并将这一范围划分成几个子范围，也就是桶
- 将待排序的一组数，分档规入这些子桶，并将桶中的数据进行排序
- 将各个桶中的数据有序的合并起来
3.举个例子：
设有数组 array = [29, 25, 3, 49, 9, 37, 21, 43]
那么数组中最大数为 49
先设置 5 个桶
那么每个桶可存放数的范围为：0~9，10~19，20~29，30~39，40~49
然后分别将这些数放人自己所属的桶
然后，分别对每个桶里面的数进行排序
或者在将数放入桶的同时用插入排序进行排序
最后，将各个桶中的数据有序的合并起来
基数排序：
1.原理：
桶排序的拓展（我没看出来这两者的联系喵喵喵？
将整数按位数切割成不同的数字，然后按每个位数分别比较。
2.过程：
首先，将要比较的数值统一成同样的数位长度（数位少的在前面补0）
然后，从最低位开始，依次进行一次排序
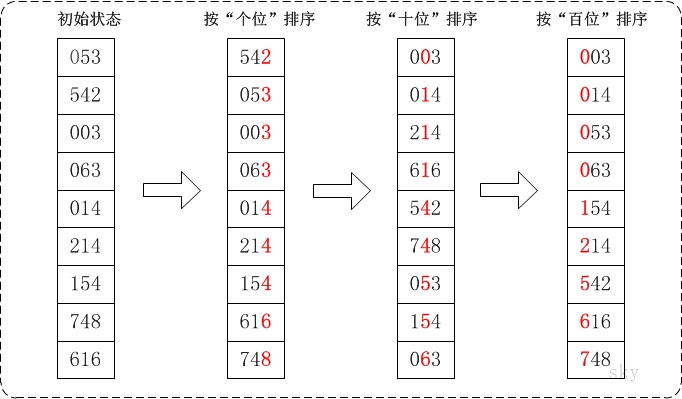
3.再举个栗子（假装图文并茂嘿嘿嘿...
通过基数排序对数组{53, 3, 542, 748, 14, 214, 154, 63, 616}，它的示意图如下：
计数排序：
1.原理：
把需要排序的数组 分到有限的桶里
2.过程：
假设有一个a数组，其中装着要排序的数列
a数列的数据范围为[x,y)
创建一个大小为y的桶数组r
将容量为y的桶数组中的每一个单元都看作一个独立的"桶"
遍历每个数组a
a的值为r数组的下标
并将该桶存的数值+1
3.又举个栗子：
a[3] = 5
r[5]++;
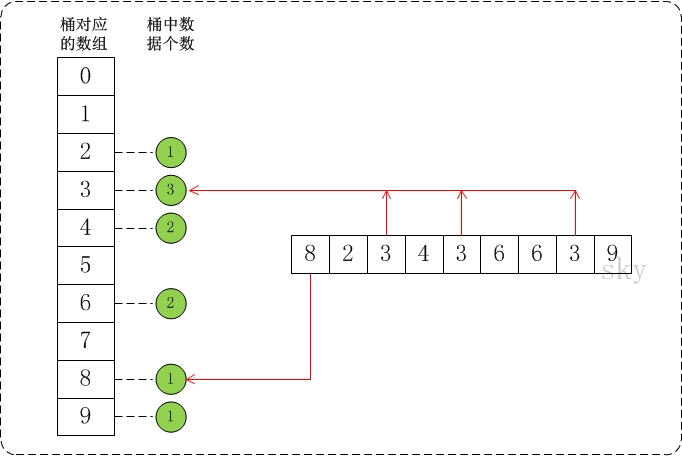
假设a={8,2,3,4,3,6,6,3,9}, max=10。
此时，将数组a的所有数据都放到需要为0-9的桶中。如下图：
