LCA--倍增法
一般来求LCA有3种方法
1.倍增
2.RMQ+欧拉序
3.tarjan(离线)
本文将倍增求lca
这个算法是很常见很常见的
也是较好理解的
(我也不明白假期学长讲的时候我为什么死活都不明白
自闭qwq
对不起学长qwq
明明学长讲的是最好的qwq
想学长了qwq)
---------------------------------------------------------------------------
一、基础概念
LCA定义:
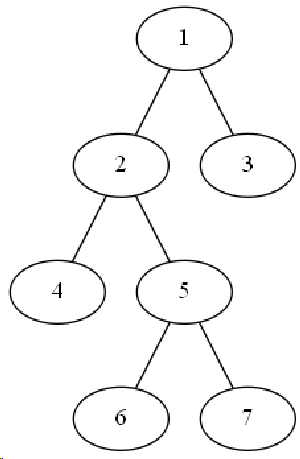
LCA(Lowest Common Ancestors),即最近公共祖先,是指在有根树中,找出某两个结点u和v最近的公共祖先。
如图,结点4,6的公共祖先有1、2,但最近的公共祖先是2,即Lca(4,6) = 2
显然遇到这个问题
首先会想到暴力
再一算
时间复杂度"仅仅"是O(n)而已啦
可是如果有q次询问呢
比如说洛谷板子题
n和q(这里的q即板子题中的m都是5 * 105的级别的
那么n*q就是一个不小的数了
那么暴力一定是过不了的了
那么就只能优化优化了
--------------------------------------------------------------------
倍增法:
注意到u,v走到最近公共祖先w之前,u,v所在结点不相同。
而到达最近公共祖先w后,再往上走仍是u,v的公共祖先,即u,v走到同一个结点,这具有二分性质。
于是可以预处理出一个2k的表,
fa[k][u]表示u往上走2k步走到的结点,令根结点深度为0,则2k>depth[u]时,令fa[k][u]=-1(不合法情况的处理)
不妨假设depth[u] < depth[v]
①将v往上走d = depth[v] - depth[u]步,此时u,v所在结点深度相同,该过程可用二进制优化。
由于d是确定值,将d看成2的次方的和值,d = 2k1 + 2k2 + ... + 2km,利用fa数组,如v = fa[k1][v],v = fa[k2][v]加速。
②若此时u = v,说明Lca(u,v)已找到
③利用fa数组加速u,v一起往上走到最近公共祖先w的过程。
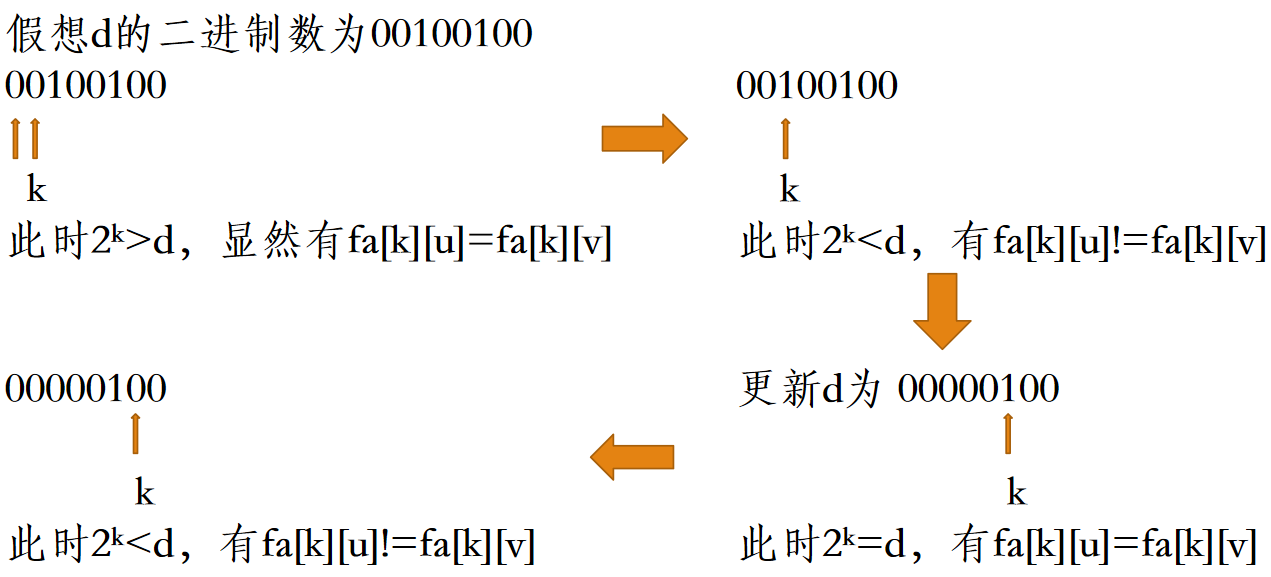
令d = depth[u] - depth[w],虽然d是个未知值,但依然可以看成2的次方的和。
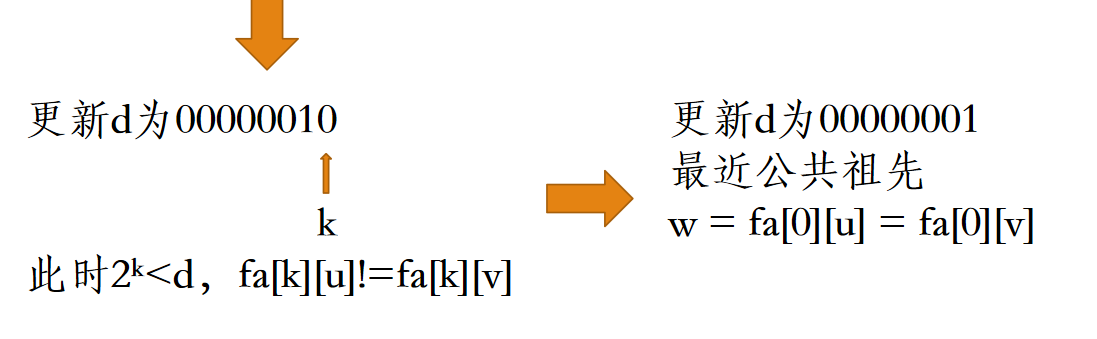
从高位到低位枚举d的二进制位,设最低位为第0位,若枚举到第k位,有fa[k][u] != fa[k][v],则令u = fa[k][u],v = fa[k][v]。
最后
最近公共祖先w = fa[0][u] = fa[0][v],即u和v的父亲
如何预处理?
k=0时,fa[k][u]为u在有根树中的父亲,令根结点fa[k][root]=-1。
k>0时,fa[k][u]=fa[k-1][fa[k-1][u]]。树的高度最多为n,k是logn级别。
时间复杂度?
预处理O(nlogn)
单次查询O(logn)
来个板子题也很好理解呀(传送门)
上面提到过的
罗姑上也有板子题
但是我最近是由hdu的oj写的
正好还有那个的代码就直接拿过来了
#include<cstdio> #include<iostream> #include<cstring> #define maxn 40000 using namespace std; struct EDGE { int nxt,to,v; }edge[maxn*2+5]; //链式前向星(可以用结构体,也可以用独立的数组) //注意这里结构体的大小,下面会说的 int T,n,root,cnt,m; //T次模拟,cnt为边的个数(边的编号),n个点的树,m次询问,root是树的根(有的lca中没有给出根节点的标号,需要自己找,这里就没给) int head[maxn+5],dep[maxn+5],dis[maxn+5]; //head也是属于链前中的内容,写在这里因为[]中为点的标号,所以它的大小就是节点数的大小 //dep存每个节点的深度,dis存每个节点到根节点的深度 int f[maxn+5][25];//前面的[i]为i节点 ,后面的[j]为从i节点往上跳2^j个节点 bool vis[maxn+5];//用来找根节点特意开的一个数组 void add(int x,int y,int z)//加边(用链式前向星存边) { edge[++cnt].to=y; edge[cnt].v=z; edge[cnt].nxt=head[x]; head[x]=cnt; } void dfs(int u,int fa) { dep[u]=dep[fa]+1;//深度加一 for(int i=0; i<=22; i++)//预处理,处理出u节点蹦2^i个节点所到达的节点编号 { f[u][i+1]=f[f[u][i]][i]; } for(int i=head[u]; i; i=edge[i].nxt)//遍历他的出边(dfs) { if(edge[i].to==fa) { continue; }//(因为正反都加边了)如果这个边指向的点是u节点的父节点,不dfs这个 dis[edge[i].to]=dis[u]+edge[i].v;//距离 f[edge[i].to][0]=u;//父节点 dfs(edge[i].to,u); } } int LCA(int x,int y) { if(dep[x]<dep[y]) { swap(x,y); }//使x是最深的那个点 for(int i=22; i>=0; i--) { if(dep[f[x][i]]>=dep[y])//如果蹦的话x的深度仍比y的深度深,那就蹦,否则不蹦 { x=f[x][i]; } if(x==y)//如果x蹦到了y,那么此时的x(也就是y)就是lca { return x; } } //此时x和y的深度相同,但不是同一个节点 for(int i=22; i>=0; i--) { if(f[x][i]!=f[y][i])//如果x和y蹦完了到了相同的节点,那么蹦到的节点一定大于或等于lca {//所以只有蹦到了不同的节点,才可以蹦(这样才能保证没蹦超出lca) x=f[x][i]; y=f[y][i]; } } return f[x][0];//离真正的lca只差一步(此时不管蹦多少都超,所以前面的循环只能使x是离lca只差一层的节点) } int main() { scanf("%d",&T); while(T--)//T次模拟(每次询问都是用新的树,因此要把之前的数组全部清空) { memset(vis,0,sizeof(vis)); memset(edge,0,sizeof(edge)); memset(f,0,sizeof(f)); memset(dep,0,sizeof(dep)); memset(head,0,sizeof(head)); memset(dis,0,sizeof(dis)); cnt=0; scanf("%d%d",&n,&m); for(int i=1; i<=n-1; i++) { int x,y,z; scanf("%d%d%d",&x,&y,&z); vis[y]=1; add(x,y,z); add(y,x,z);//因为不知道x和y谁是爸爸,所以就正反都加边 ,所以结构体的大小要开两倍 } for(int i=1; i<=n; i++) { if(vis[i]==0) { root=i; break; } }//没有被标记过的是根节点 dfs(root,0); for(int i=1; i<=m; i++) { int a,b; scanf("%d%d",&a,&b); printf("%d\n",dis[a]+dis[b]-2*dis[LCA(a,b)]); } } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号