树链剖分

 

模板题

 

支持的操作：

操作1： 格式： 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z

操作2： 格式： 2 x y 表示求树从x到y结点最短路径上所有节点的值之和

操作3： 格式： 3 x z 表示将以x为根节点的子树内所有节点值都加上z

操作4： 格式： 4 x 表示求以x为根节点的子树内所有节点值之和

 

为什么要用树链剖分呢？？？

因为（看板子看板子），题目它给你了一棵树，而它很难是一棵二叉树

所以很难用线段树来实现

所以我们要选一个折中的办法

是平均起来询问的连续区间数量最少

 

实质：

通过改变dfs序，使得能做树上线段树（啊哈？？这是什么鬼？？emm...可以先不管...一会儿可能就会知道了）

 

一些个概念：

重儿子：对于每一个非叶子节点，它的儿子中 以那个儿子为根的子树节点数最大的儿子 为该节点的重儿子

轻儿子：父亲节点中除了重结点以外的结点；

（叶子结点没有重儿子也没有轻儿子，因为它没有儿子）

重边：父亲结点和重结点连成的边；

轻边：父亲节点和轻节点连成的边；

重链：由多条重边连接而成的路径；

轻链：由多条轻边连接而成的路径；

[

　　对于叶子节点，若其为轻儿子，则有一条以自己为起点的长度为1的链

　　每一条重链以轻儿子为起点

]

 

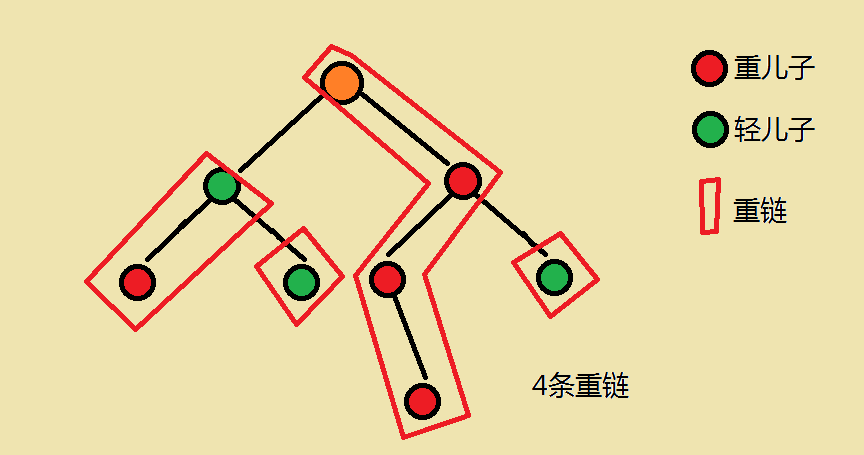
（借一个图过来，嘻嘻）

 

这里涉及到两个dfs

 

dfs1：

这个dfs要处理几件事情：

　　　　标记每个点的深度dep[ ]

　　　　标记每个点的父亲fa[ ]

　　　　标记每个非叶子结点的子树大小（含它自己）

　　　　标记每个非叶子结点的重儿子编号son[ ]

 

 

void dfs1(int o,int f,int deep)//o是当前节点，f是o节点的父亲，deep是o节点的深度
{
    dep[o] = deep;//记录每个点的深度
    fa[o] = f;//记录每个非叶子节点的父亲
    siz[o] = 1;//记录每个非叶子节点的子树大小，因为有它自己，所以初始值为1
    int maxson = -1;//记录中儿子的儿子数
    for(int i = 1;i;i = nex[i])//遍历o点的出边
    {
        int u = to[o];
        if(u == f)//若为父亲则continue（向上遍历啦？？！）
            continue;
        dfs1(u,o,deep+1);//dfs1下去
        siz[o] += siz[u];//把它儿子的子树大小加到它身上去
        if(siz[u] > maxson)
        {
            son[o] = u;//如果找到了比当前找到的重儿子树还大的子树，就替换掉之前的重儿子
            maxson = siz[u];
        }
    }
}

 

 

 

dfs2：

这个dfs要处理的几件事情：

　　　　标记每个点的新编号

　　　　复制每个点的初始值到新编号上

　　　　处理每个点所在链的顶端

　　　　处理每条链

顺序：先处理重儿子再处理轻儿子

 

void dfs2(int o,int topf)//o是当前节点，topf是当前链的最顶端的节点
{
    id[o] = ++cnt;//标记每个点的新编号
    wt[cnt] = w[o];//把每个点的初始值赋到新编号上来
    top[o] = topf;//这个点所在链的顶端
    if(!son)//如果没有儿子，就返回
        return;
    dfs2(son[o],topf);//按 先处理重儿子，再处理轻儿子 的递归顺序处理
    for(int i = beg[o];i;i = nex[i])
    {
        int u = to[i];
        if(y == fa || y == son[o])
            continue;
        dfs(u,u);//对于每一个轻儿子都有一条从他自己开始的链
    }
}

 

 

用图来模拟一下dfs2的顺序和结果：

（嘿嘿，又偷了一张图）

 

注意：

　　因为顺序是先重后轻，所以每一条重链的新编号是连续的

　　因为是dfs，所以每一个子树的新编号也是连续的

 

现在回顾一下我们要处理的问题：

　　处理任意两点间路径上的点权和

　　处理一点及其子树的点权和

　　修改任意两点间路径上的点权

　　修改一点及其子树的点权

 

1.处理任意两点间路径时：

规定：让连顶端的深度更深的那个点为x（让这个点先往上跳）

（这是为什么呢？？！）

• ans加上x点到x所在连顶端这一段区间的点权和
• 把x跳到x所在链顶端的那个点的上面一个点

不停地之行这两个步骤，直到两个点处于一条链上，这时再加上此时连个点的区间和即可

这是会发现，我们所要处理的所有曲建军为连续编号（新编号）

于是想到用线段树（终于明白了上面说的树上树）

用线段树处理连续编号区间和

每次查询时间复杂度为O（log²n）

 

int qrange(int x,int y)//查询x到y之间 
{
    int ans = 0;//总和 
    while(top[x] != top[y])//当两个点不再同一条链上 
    {
        if(dep[top[x]] < dep[top[y]])//把x点改为所在链顶端的深度更深的那个点 
            swap(x,y);
            res = 0;
            query(1,1,n,id[top[x]],id[x]);//ans加上x点到x所在连顶端 这一段区间的点权和 
            ans += res;
            ans %= mod;//按题意取模 
            x = fa[top[x]];//把x跳到x所在连顶端的那个点上面的一个点 
    }
    //知道两个点处在一条链上 
    if(dep[x] > dep[y])
        swap(x,y);
    res = 0;
    query(1,1,n,id[x],id[y]);//这时再加上此时两个点的区间和即可 
    ans += res;
    return ans % mod;
}

 

2.处理一点及其子树的点权和：

因为：记录了每个非也子节点的子树大小（含他自己），并且每个子树的新编号都是连续的

于是

直接线段树区间查询即可

时间复杂度O(logn)

//区间查询
int qson(int o)
{
    res = 0;
    query(1,1,n,id[x],id[x] + siz[x] - 1);//子树区间右端点为id[x] + siz[x] - 1；
    return res; 
} 

//区间修改 
void updrange(int x,int y,int k)
{
    k %= mod;
    while(top[x] != top[y])
    {
        if(dep[top[x]] < dep[top[y]])
            swap(x,y);
        update(1,1,n,id[top[x]],id[x],k);
        x = fa[top[x]];
    }
    if(dep[x] > dep[y])
        swap(x,y);
    update(1,1,n,id[x],id[y],k);
}

//子树修改 
void updson(int x,int k)
{
    update(1,1,n,id[x],id[x] + siz[x] - 1,k);
}

emm...

基本差不多了呢

就差板子的完整代码啦！！！

 

我心态崩了...

qwqqwq

写跪了

到现在还de不出来bug

 

7.29

我没想到这次我咕了这么久

而且...我几乎彻底把它忘了

其实板子几天前就搞完了

（轻松了很多）

于是我又新写了一个极其不完整的博客？

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

inline int read()
{
    int sum = 0,p = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
            p = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        (sum *= 10) += ch - '0';
        ch = getchar();
    }
    return sum * p;
}

#define mid ((l + r) >> 1)
#define len (r - l + 1)
#define lson o << 1,l,mid
#define rson o << 1 | 1,mid + 1,r

const int maxn = 2e5 + 5,maxm = 1e5 + 5;
int n,m,r,p;
int val[maxn],dep[maxn],fa[maxn],siz[maxn],son[maxn],id[maxn],nval[maxn],top[maxn];
//val点权 ,dep点深度 ,fa父节点编号，siz子树大小,son重儿子,id新编号,nval新编号下的点权数，top当前链顶端结点 
int res,tot,lazy[maxn * 4],a[maxn * 4];
int cnt,head[maxn]; 
struct edge
{
    int nxt,to;
}e[maxm * 4];

void add(int a,int b)
{
    e[++cnt].nxt = head[a];
    e[cnt].to = b;
    head[a] = cnt;
}

void dfs1(int o,int f,int deep)//o当前结点，f父节点，deep深度 
{
    dep[o] = deep;
    fa[o] = f; 
    siz[o] = 1; 
    int maxson = -1;
    for(int i = head[o];i;i = e[i].nxt)
    {
        int v = e[i].to;
        if(v == f)
            continue;
        dfs1(v,o,deep+1);
        siz[o] += siz[v];
        if(siz[v] > maxson)
        {
            son[o] = v;
            maxson = siz[v];
        }
    } 
}

void dfs2(int o,int topf)
{
    id[o] = ++tot;
    nval[tot] = val[o];
    top[o] = topf;
    if(!son[o])
        return;
    dfs2(son[o],topf);
    for(int i = head[o];i;i = e[i].nxt)
    {
        int v = e[i].to;
        if(v == fa[o] || v == son[o])
            continue;
        dfs2(v,v);
    } 
}

//---------------线段树---------------- 

void pushdown(int o,int lenn)
{
    lazy[o << 1] += lazy[o];
    lazy[o << 1 | 1] += lazy[o];
    a[o << 1] += lazy[o] * (lenn - (lenn >> 1));
    a[o << 1 | 1] += lazy[o] * (lenn >> 1);
    a[o << 1] %= p;
    a[o << 1 | 1] %= p;
    lazy[o] = 0;
}

void build(int o,int l,int r)
{
    if(l == r)
    {
        a[o] = nval[l] % p;
        return;
    }
    build(lson);
    build(rson);
    a[o] = (a[o << 1] + a[o << 1 | 1])% p;
}

void update(int o,int l,int r,int ql,int qr,int k)
{
    if(ql <= l && r <= qr)
    {
        lazy[o] += k;
        a[o] += k * len;
        return;
    }
    if(lazy[o])
        pushdown(o,len);
    if(ql <= mid)
        update(lson,ql,qr,k);
    if(qr > mid)
        update(rson,ql,qr,k);
    a[o] = (a[o << 1] + a[o << 1 | 1])%p;
}

void query(int o,int l,int r,int ql,int qr)
{
    if(ql <= l && r <= qr)
    {
        res = (res +a[o])%p;
        return;
    }
    if(lazy[o])
        pushdown(o,len);
    if(ql <= mid)
        query(lson,ql,qr);
    if(qr > mid)
        query(rson,ql,qr);
}

//---------------线段树—————————————— 

void updr(int l,int r,int k)
{
    k %= p;
    while(top[l] != top[r])
    {
        if(dep[top[l]] < dep[top[r]])
            swap(l,r);
        update(1,1,n,id[top[l]],id[l],k);
        l = fa[top[l]];
    }
    if(dep[l] > dep[r])
        swap(l,r);
    update(1,1,n,id[l],id[r],k);
}

int queryr(int l,int r)
{
    int ans = 0;
    while(top[l] != top[r])
    {
        if(dep[top[l]] < dep[top[r]])
            swap(l,r);
        res = 0;
        query(1,1,n,id[top[l]],id[l]);
        ans = (ans + res)%p;
        l = fa[top[l]];
    }
    if(dep[l] > dep[r])
        swap(l,r);
    res = 0;
    query(1,1,n,id[l],id[r]);
    return (ans + res) % p;
}

void updson(int o,int k)
{
    update(1,1,n,id[o],id[o] + siz[o] - 1,k);
}

int qson(int o)
{
    res = 0;
    query(1,1,n,id[o],id[o] + siz[o] - 1);
    return res;
}

int main()
{
    n = read(),m = read(),r = read(),p = read();
    for(int i = 1;i <= n;i++)
        val[i] = read();
    for(int i = 1;i < n;i++)
    {
        int a = read(),b = read();
        add(a,b);
        add(b,a);
    }
    dfs1(r,0,1);
    dfs2(r,r);
    build(1,1,n); 
    while(m--)
    {
        int opt = read();
        if(opt == 1)
        {
            int x = read(),y = read(),z = read();
            updr(x,y,z);
        }
        else if(opt == 2)
        {
            int x = read(),y = read();
            printf("%d\n",queryr(x,y));
        }
        else if(opt == 3)
        {
            int x = read(),y = read();
            updson(x,y);
        }
        else
        {
            int x = read();
            printf("%d\n",qson(x));
        }
    }
    return 0;
}