st表

几个月之前学的

当时

可能只是明白了

但没有真正的掌握

以至与

现在的我

不记得多少了

所以

我觉得很有必要

写一写

-------------------------------

st表

• 用于解决RMQ问题（区间最值问题）
• O（n logn）

 

ST表是利用的是倍增的思想

拿最大值来说

我们用Max[i][j] Max[i][j] 表示，从i i 位置开始的2 j  2j 个数中的最大值，例如Max[i][1] Max[i][1] 表示的是i i 位置和i+1 i+1 位置中两个数的最大值

那么转移的时候我们可以把当前区间拆成两个区间并分别取最大值（注意这里的编号是从1 1 开始的）

 

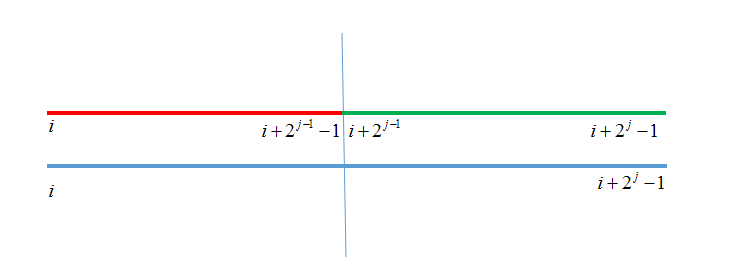
查询的时候也比较简单

我们计算出log 2 (区间长度) log2(区间长度)

然后对于左端点和右端点分别进行查询，这样可以保证一定可以覆盖查询的区间

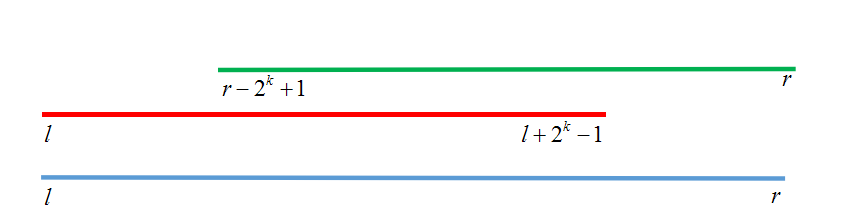
刚开始学的时候我不太理解为什么从右端点开始查的时候左端点是r−2 k +1

实际很简单，因为我们需要找到一个点x  ，使得x+2 k −1=r

这样的话就可以得到x=r−2 k +1

上面讲的可能比较抽象，建议大家画个图好好理解一下

-----------------------------------------------------------------------------------

题目背景

这是一道ST表经典题——静态区间最大值

请注意最大数据时限只有0.8s，数据强度不低，请务必保证你的每次查询复杂度为 O(1)O(1) O(1)

题目描述

给定一个长度为 N N N 的数列，和 M M M 次询问，求出每一次询问的区间内数字的最大值。

输入输出格式

输入格式：

 

第一行包含两个整数 N,M N, M N,M ，分别表示数列的长度和询问的个数。

第二行包含 N N N 个整数（记为 ai a_i ai​），依次表示数列的第 ii i 项。

接下来 M M M行，每行包含两个整数 li,ril_i, r_i li​,ri​，表示查询的区间为 [li,ri][ l_i, r_i] [li​,ri​]

 

输出格式：

 

输出包含 MM M行，每行一个整数，依次表示每一次询问的结果。

 

输入输出样例

输入样例#1： 复制

8 8
9 3 1 7 5 6 0 8
1 6
1 5
2 7
2 6
1 8
4 8
3 7
1 8

输出样例#1： 复制

9
9
7
7
9
8
7
9

说明

对于30%的数据，满足： 1≤N,M≤10 

对于70%的数据，满足： 1≤N,M≤10^5 

对于100%的数据，满足： 1≤N≤10^5,1≤M≤10^6,ai∈[0,10^9],1≤li≤ri≤N

 

--------------------------------------------------------------------------------------------------------------

莫名tle

心情烦躁

只好谟大佬了

#include<bits/stdc++.h>
#define N 200000
#define LN 20   //2的ln次方已经足够了 
using namespace std;
int n,m,a[N],f[N][LN+5],lo[N],x,y,s;  //数组稍稍开大一点点比较好 
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    lo[0]=-1;
    for(int i=1;i<=n;i++){
        f[i][0]=a[i];
        lo[i]=lo[i>>1]+1;   //i在这里代表长度 这个循环是计算出每个长度对应的2^t的t 
    }
    for(int j=1;j<=LN;j++)
        for(int i=1;i+(1<<j)-1<=n;i++)  //因为后一段的开始是r-2^k+1 也就是r-lo[l-r+1] 防止越界 
            f[i][j]=max(f[i][j-1],f[i+(1<<j-1)][j-1]);  //预处理 计算出每种情况的max 
    while(m--){
        scanf("%d%d",&x,&y);
        s=lo[y-x+1];  
        printf("%d\n",max(f[x][s],f[y-(1<<s)+1][s]));  // 查询时复杂度为O(1) 
    }
    return 0;
}