结对项目第一周
结对项目——四则运算 阶段性总结
需求分析(第一周达成):
- 能够生成n道四则运算题,n可由使用者输入来控制
- 支持整数
- 支持分数
- 生成题目中含有括号
- 可以判断正误,如果错误会输出正确答案
- 统计正确率
扩展需求:
- 生成题目后存入文件
- 完成题目后从文件读入并进行判断
- 支持题目去重
- 支持
繁體中文,简体中文,English
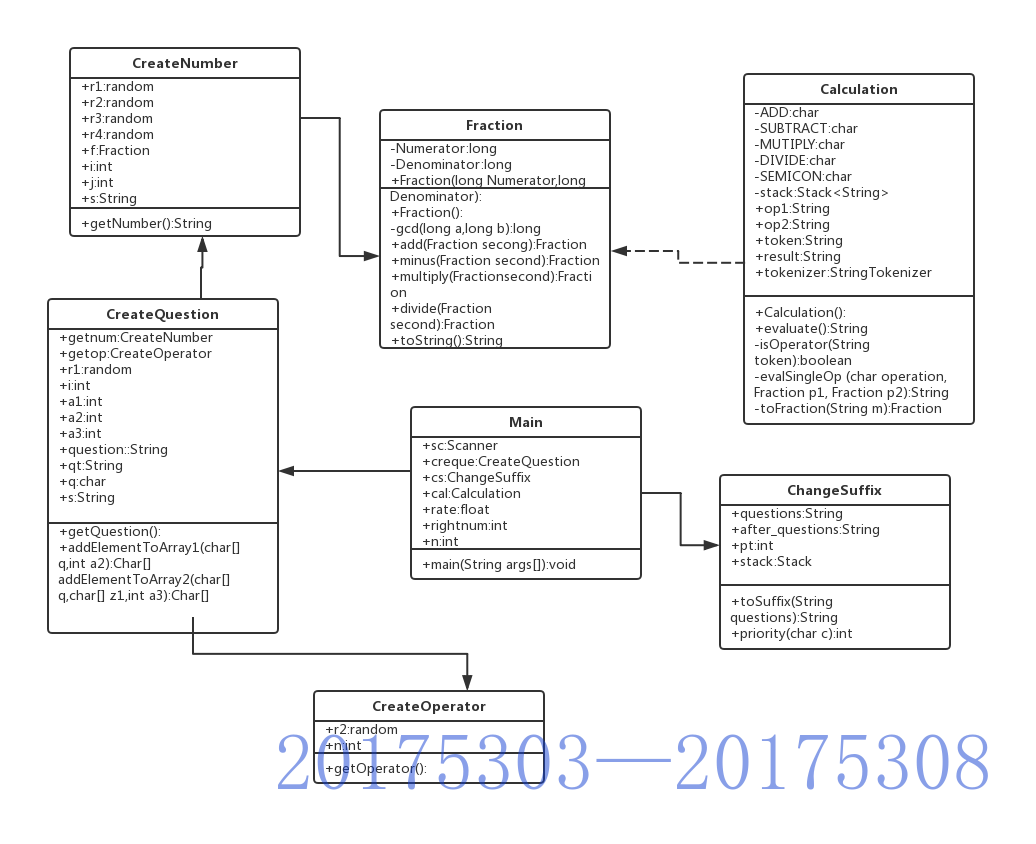
设计思路(同时输出UML类图):
以下是程序主体设计思路,各步骤具体操作详情请见注释:
由于本周可用的准备时间较长,我们选择直接进行真分数的操作。在java语言中并没有一个专门的类用来表示分数,所以需要手动添加。我们设计了一个专门的类用来描述分数(程序中的Fraction类),并且严格依照分数的性质来进行设计(例如分母不可以为0),其次我们要给出分数四则运算的计算方法。然后我们考虑的是,进行四则运算,要随机生成题目,我们选择分别建两个类,一个用来生成操作数(分数随机生成两个数字,分别做分子和分母),一个用来生成符号,生成的随机性我们通过random()来保证。写好了这两个类之后,我们用另一个专门生成题目的类来调用这两个类中的方法组成题目。转后缀码后进行计算。最后统计结果。
实现过程中的关键代码解释:
在整体项目的实现过程中,由于结对队友前期公务繁忙,所以我承担了主要的代码编写工作,所以在最后注释由队友添加,这样在他添加注释的过程中也重新审视了一遍代码
分数类代码:
public class Fraction {
private long Numerator; // 分子
private long Denominator; // 分母
public Fraction(long Numerator, long Denominator) {
this.Numerator = Numerator; //将传过来的参数Numerator赋值给类中的Numerator
if (Denominator == 0) {
throw new ArithmeticException("分母不能为零"); //如果分母为0,抛出问题“分母不能为零”
} else {
this.Denominator = Denominator; //如果分母不为0,将传过来的参数Denominator赋值给类中的Denominator
}
change(); //对分数进行化简
}
public Fraction() { //将分数初始化
this(0, 1);
}
public long getNumerator() { //返回分子Numerator
return Numerator;
}
public void setNumerator(long numerator) {
Numerator = numerator; //设置分子,将传过来的参数numerator赋值给类中的Numerator
}
public long getDenominator() {
return Denominator; //返回分母Denominator
}
public void setDenominator(long denominator) {
Denominator = denominator; //设置分母,将传过来的参数denominator赋值给类中的Denominator
}
private Fraction change() {
long gcd = gcd(Numerator,Denominator); //求分子和分母的最大公因子并将公因子的值赋给gcd
Numerator /= gcd; //将分子Numerator的值除以gcd的值赋给Numerator
Denominator /= gcd; //将分母Denominator的值除以gcd的值赋给Denominator
return this;
}
private long gcd(long a, long b) { //求a和b的最大公因数
long mod = a % b;
if (mod == 0) {
return b; //如果余数mod为0,返回除数即为最大公因数
} else {
return gcd(b, mod); //如果余数mod不等于0,将除数b看做被除数,把余数看做除数递归调用gdc(b,mod)
}
}
public Fraction add(Fraction second) { //一个分数加一个分数的加法法则
return new Fraction(this.Numerator * second.Denominator + second.Numerator * this.Denominator,
this.Denominator * second.Denominator);
}
public Fraction minus(Fraction second) { //一个分数减一个分数的减法法则
return new Fraction(this.Numerator * second.Denominator - second.Numerator * this.Denominator,
this.Denominator * second.Denominator);
}
public Fraction multiply(Fraction second) { //一个分数乘一个分数的乘法法则
return new Fraction(this.Numerator*second.Numerator,
this.Denominator * second.Denominator);
}
public Fraction divide(Fraction second) { //一个分数除以一个分数的除法法则
return new Fraction(this.Numerator*second.Denominator,
this.Denominator * second.Numerator);
}
public String toString() { //讲分数以字符串的形式返回
if(this.Denominator==1){
return String.format("%d",this.Numerator); //如果分母为1,输出分子
}
else {
return String.format("%d/%d", this.Numerator, this.Denominator); //如果分母不为1,输出"分子/分母"
}
}
}
生成题目代码:
import java.util.*;
public class CreateQuestion{
public static String getQuestion(){ //得到一个String类型的问题
CreateNumber getnum = new CreateNumber(); //新建一个CreateNumber类的对象getnum
CreateOperator getope = new CreateOperator(); //新建一个CreateOperator类的对象getope
Random r1 = new Random();
String s = new String();
int i,a1,a2,a3;
a1 = r1.nextInt(4); //随机生成一个[0,4)的数a1,这决定了公式的长度
String question,qt;
question=getnum.getNumber() + getope.getOperator(); //初始化变量question
for(int j=1;j<=a1;j++){
qt=getnum.getNumber()+getope.getOperator();
question=question+qt; //循环增加问题长度
}
question= question+getnum.getNumber(); //给问题的最后加上一个数
char[] q = question.toCharArray(); //将生成的字符串变成字符数组,以便在里边加括号
if(q.length>9){ // 字符串的长度在9以上才会进行加括号操作,避免出现因找不到加括号的位置而出现死循环的情况
for(i=0;;i++){ //通过循环找寻适合加左括号的位置
a2=r1.nextInt(q.length-3); //随机生成一个位置的下标,在排除最后3个字符的字符串里找位置生成左括号,以便留给右括号空间
if(a2<=5){
if(q[a2]=='+' || q[a2]=='-' || q[a2]=='*' || q[a2]=='÷'){
break; //若找到合适位置便退出循环
}
else continue; //未找到则继续循环
}
}
char[] z1=addElementToArray1(q,a2); //调用方法,把字符数组q[],位置a2传到方法里边
for(i=0;;i++){ //通过循环找寻适合加右括号的位置
a3=r1.nextInt(z1.length); //随机生成一个位置的下标,找位置生成右括号
if(a3>a2+4){ //右括号的位置应该比左括号的位置靠右至少4位
if( z1[a3]=='+' || z1[a3]=='-' || z1[a3]=='*' || z1[a3]=='÷' || a3==q.length){
break; //若找到合适位置便退出循环
}
else continue; //未找到则继续循环
}
}
char[] z2=addElementToArray2(q,z1,a3); //调用方法,把字符数组q[],z1[],位置a2传到方法里边
s = new String(z2);
return s;
}
else s = new String(q);
return s;
}
public static char[] addElementToArray1(char[] q,int a2) {
char [] z1 = new char[q.length+1]; //字符数组z1长度相比q加一
int i;
for(i=z1.length-1;i>a2;i--){
z1[i]=q[i-1];
}
z1[a2+1]='(';
for(i=0;i<=a2;i++){
z1[i]=q[i];
} //在q[]中a2位置加入左括号,写入z1[]
return z1;
}
public static char[] addElementToArray2(char[] q,char[] z1,int a3) {
char [] z2 = new char[z1.length+1]; //字符数组z2长度相比z1加一
int i;
if(z1[a3]=='+' || z1[a3]=='-' || z1[a3]=='*' || z1[a3]=='÷'){
for(i=z2.length-1;i>a3;i--){
z2[i]=z1[i-1];
}
z2[a3]=')';
for(i=0;i<=a3-1;i++){
z2[i]=z1[i];
}
} //若a3位置为一个运算符,在z1[]中a3位置加入左括号,写入z2[]
else {
for(i=0;i<z1.length;i++){
z2[i]=z1[i];
}
z2[z1.length]=')';
} //若a3等于字符数组q的长度,将z1写入z2,并在z2末尾加上右括号
return z2;
}
}
转后缀式代码:
import java.util.*;
public class ChangeSuffix {
String questions;
String after_questions= "";
public String toSuffix(String questions){
this.questions=questions;
Stack stack=new Stack(); //新建一个栈
for (int i=0;i<questions.length();i++) {
char ele=questions.charAt(i); //取出字符串的第i个字符
if (ele>='0'&&ele<='9'){
after_questions=after_questions+ele; //如果第i个字符为数字,直接写入到后缀表达式中
}
else if (ele=='+'||ele=='-'||ele=='*'||ele=='÷'||ele=='/') {
after_questions=after_questions+" "; //如果遇到运算符
if (stack.empty()){
stack.push(ele);
} //若栈为空,字符进栈
else if (priority(ele)>priority((char)stack.peek())) {
stack.push(ele);
} //如果栈顶元素的运算优先级小于当前字符的运算优先级,当前元素进栈
else{
after_questions=after_questions+ String.valueOf(stack.pop())+" ";
i--;
} //其他情况即如果栈顶元素的运算优先级大于或等于当前字符的运算优先级,将该元素出栈,变成字符串类型
}
else if(ele=='('){
stack.push(ele);
} //如果当前元素为左括号,进栈
else if(ele==')'){
after_questions+=" ";
while((char)stack.peek()!='('){
after_questions=after_questions+ String.valueOf(stack.pop())+" ";
} //如果栈顶元素不是左括号,连续将栈顶元素弹出变成字符串类型写入到后缀表达式中
stack.pop(); //将左括号弹出
}
}
after_questions+=" ";
while(!stack.empty()){
after_questions=after_questions+String.valueOf(stack.pop())+" ";
} //如果栈顶元素非空,连续弹出栈顶元素变成字符串类型写入到后缀表达式中
return after_questions;
}
public int priority (char c){ //定义运算符的优先级
int pt =0;
switch(c){
case '(':
pt=1;
break;
case '+':
case '-':
pt=2;
break;
case '*':
case '÷':
pt=3;
break;
case '/':
pt=4;
break;
case ')':
pt=5;
break;
default:
pt=0;
break;
}
return pt;
}
}
计算代码:
import java.util.*;
public class Calculation {
/** constant for addition symbol */
private final char ADD = '+';
/** constant for subtraction symbol */
private final char SUBTRACT = '-';
/** constant for multiplication symbol */
private final char MULTIPLY = '*';
/** constant for division symbol */
private final char DIVIDE = '÷';
private final char SEMICON= '/';
/** the stack */
private Stack<String > stack;
public Calculation() {
stack = new Stack<String>(); //创建一个String类型的栈
}
public String evaluate (String expr)
{
String op1,op2;
Fraction p1;
Fraction p2;
String token;
String result ="";
StringTokenizer tokenizer = new StringTokenizer (expr); //将expr后缀表达式传进StringTokenizer方法
while (tokenizer.hasMoreTokens())
{
token = tokenizer.nextToken(); //将StringTokenizer分解出的字符串赋给token
//如果是运算符,调用isOperator
if (isOperator(token))
{
//从栈中弹出操作数2
op2=stack.pop();
p2 = toFraction(op2);
//从栈中弹出操作数1
op1=stack.pop();
p1 =toFraction(op1);
//根据运算符和两个操作数调用evalSingleOp计算result;
result=evalSingleOp(token.toCharArray()[0],p1,p2);
//计算result入栈;
stack.push(result);
}
else//如果是操作数,入栈
stack.push(token);
}
return result;
}
private boolean isOperator (String token)
{
return ( token.equals("+") || token.equals("-") ||
token.equals("*") || token.equals("÷")||token.equals("/") ); //若token是运算符,返回true
}
private String evalSingleOp (char operation, Fraction p1, Fraction p2)
{
Fraction result = new Fraction(0,1); //初始化result
switch (operation) //根据运算符选择运算
{
case ADD:
result =p1.add(p2);
break;
case SUBTRACT:
result = p1.minus(p2);
break;
case MULTIPLY:
result = p1.multiply(p2);
break;
case DIVIDE:
case SEMICON:
result = p1.divide(p2);
}
return result.toString(); //将结果变成字符串
}
private Fraction toFraction(String m){
String token1, token2;
Fraction r = new Fraction(0,1);
StringTokenizer tokenizer1 = new StringTokenizer(m, "/");//把操作数以"/"为标记分割开来
token1 = tokenizer1.nextToken();
if (tokenizer1.hasMoreTokens()) {//如果有第二个元素就把token1放在分子的位置,token2放在分母的位置
token2 = tokenizer1.nextToken();
int toke1 =Integer.valueOf(token1).intValue();
int toke2 =Integer.valueOf(token2).intValue();
r =new Fraction(toke1,toke2);
}
else {//如果没有第二个元素就把token1放在分子的位置,分母固定为1
int toke1 = Integer.valueOf(token1).intValue();
r =new Fraction(toke1,1);
}
return r;
}
}
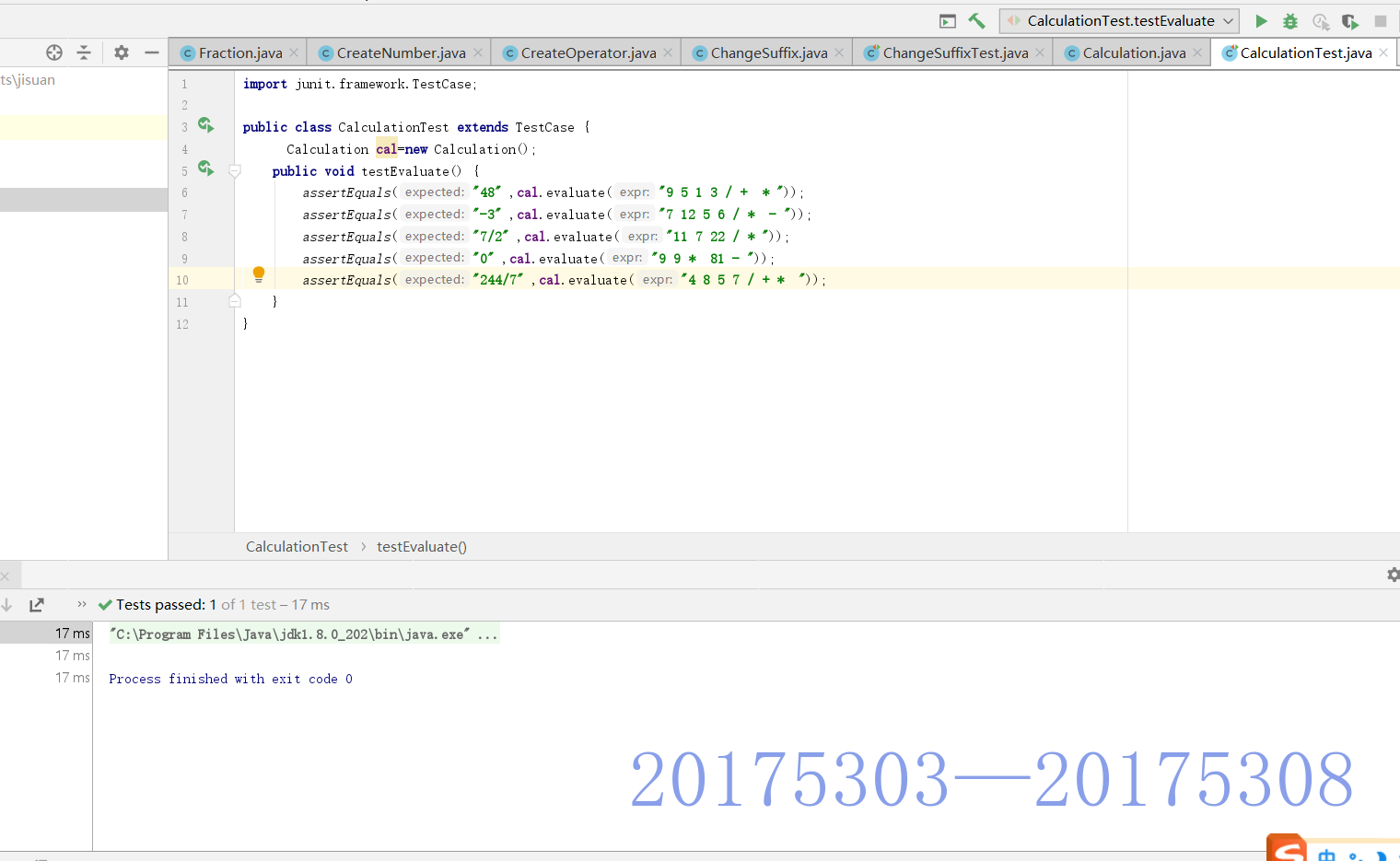
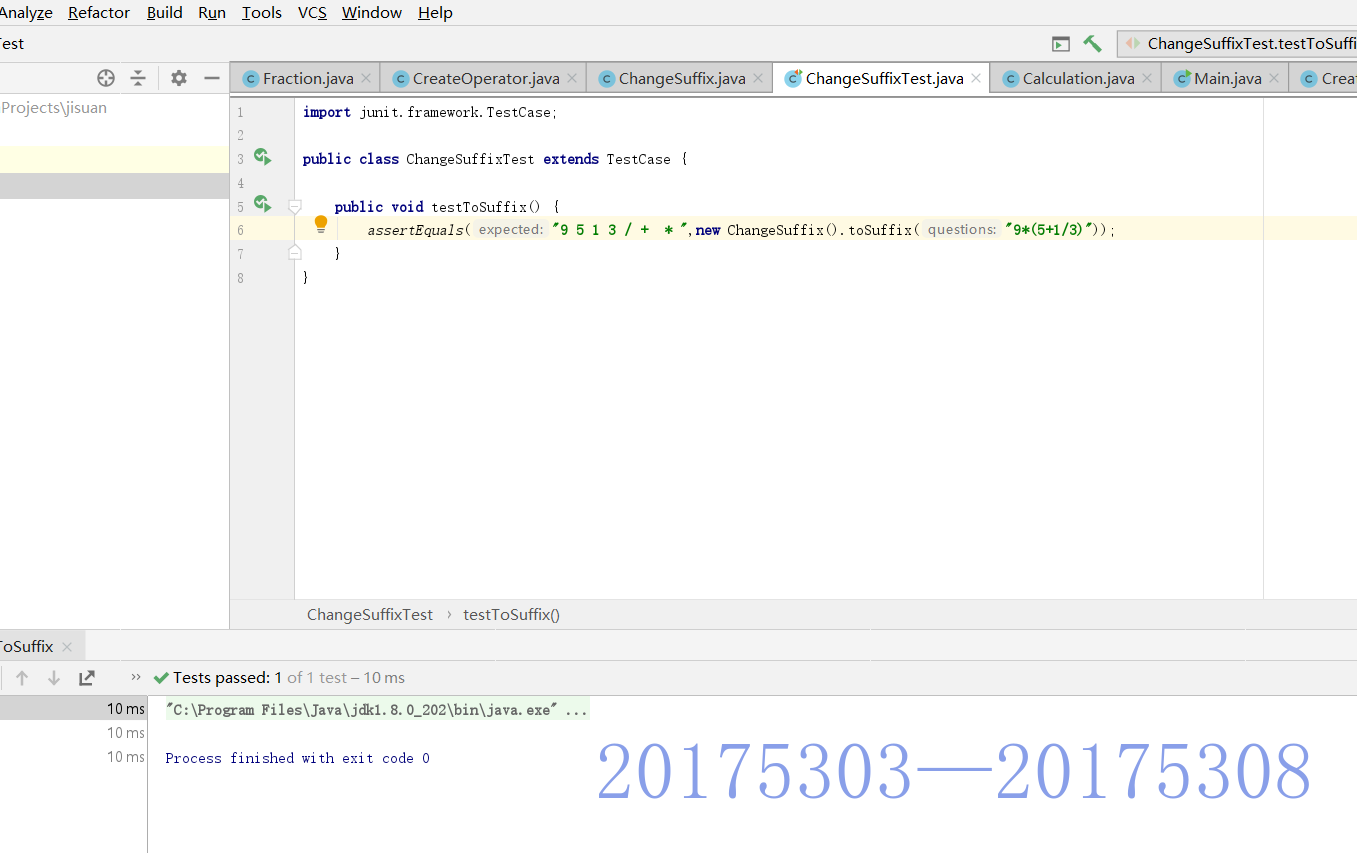
测试方法:

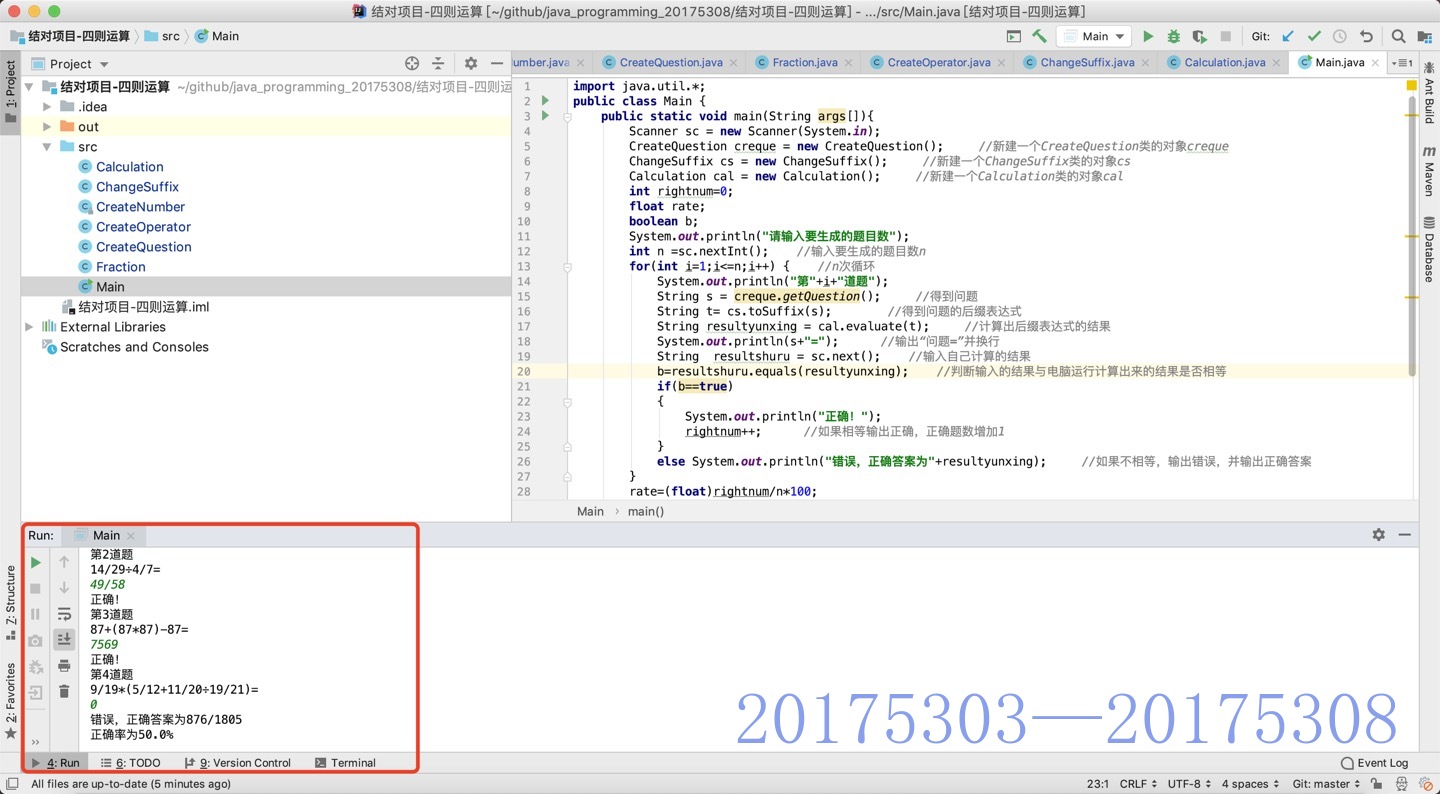
运行过程截图:
代码托管

遇到的困难及解决办法
- 在生成算式的时候,我一直找不到正确的办法,建立如getNumber()+getOperator()的形式,结尾会是运算符号,如果反过来,算式的起始又会是符号。
解决办法:其实这个问题非常好解决,只是我的思维定式让我始终跳不开一段语句完成一件事的思路,其实我大可在getNumber()+getOperator()的循环执行后再加一个getNUmber()收尾,这样生成的就会是一个正确的算式,想到了这一点突然觉得这个问题十分好笑
- 中缀式转后缀式最初是在离散数学中简单学习过但并没有太过深入的了解,所以在本次计算需要用到后缀式的时候一时间有些不知所措,代码编写进程一度停滞。
解决办法:其实在老师给的博客中有关于转后缀法则的介绍,里面的内容很详细,只需要用给出的例子算式对照每一条法则一步一步来就可以写出后缀式了
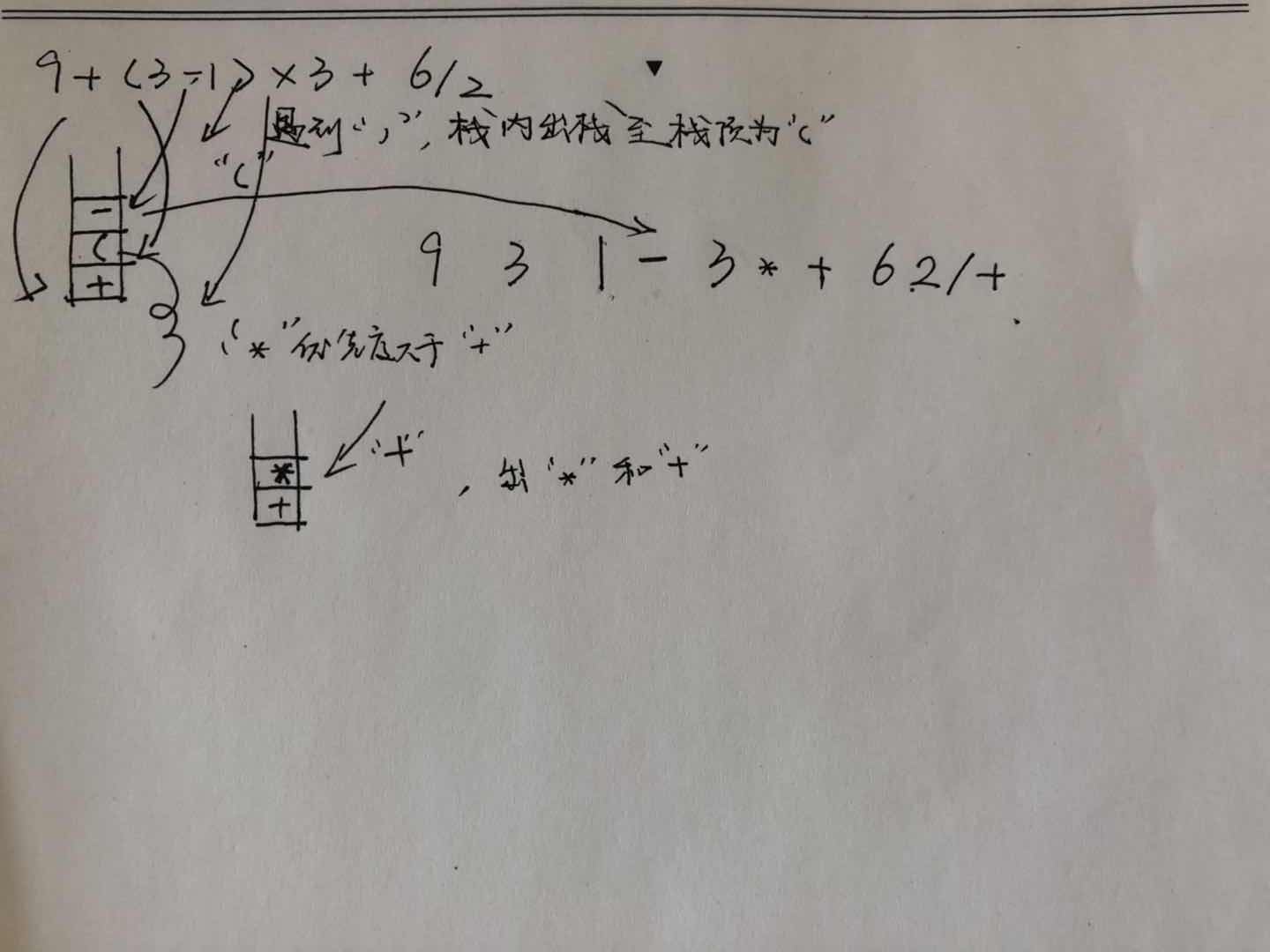
- 我一开始在设定分数类的时候,一直存在这样一种思维,如果带有分数的类进行计算出现负数,那么分解成分子分母的时候会因为不知道将符号分给分子还是分母产生错误,就强行将负数的情况锁死,结果运行的时候问题多多
解决办法:其实仔细想想,分数在运算的时候从来都没有用到分母的加减运算,分母向来只参与到通分这一步。如果分数整体表现为负数,一定是分子出现了错误,而无论栈计算还是转后缀式,负号“-”一定会和分子以字符串的形式捆绑在一起,不会产生错误。
- 问题同样出在分数类,分数有一个很重要的特点,就是他的分母不可以为0,我一直不知道如果生成了这种情况该怎么处理,就强行将分母为0的时候给分母强行改成其他值,虽然在大范围内分母为0的概率不大,但这种情况一旦出现就无法解决,知道有一次其他内容出现运行错误我点开了错误报告:(报告给出的具体内容没有截屏,现在已经无法找回当时的页面了。。。)

解决办法:在分数类仿照java原有的代码写好处理办法如下:
if (Denominator == 0) {
throw new ArithmeticException("分母不能为零");
其中的ArithmeticException就是处理方法
- 对后缀式进行计算的代码,老师博客中已经有了一个大致的样板,但是里面没有有关分数的情况,需要进一步改动,但是在改动的时候,出现了诸多错误无法一一列举,但总体解决办法如下
解决办法:Stack类型之前没有进行过学习,急于求成的我并没有系统的整体学习,但在我的使用过程中我发现Stack
对结对的小伙伴进行评价
在我们结对初始我们就认为最好的合作一定要是互补的。我很幸运,我的结对小伙伴非常靠谱,他的严谨补足了我一些不求甚解的缺点。在我们的团队合作进程中,我们分工比较明确。我进行了程序的主要的代码编写工作,但是在一些细节的完善和一些问题的解决过程中他提出了非常宝贵的建议和思路,包括一些程序的重要补足。在结对的过程中,我们考虑的应该不仅是如何更好的进行一个项目的编写,还要在进程中不断学习对方身上的优点。我觉得我的结对伙伴是个值得信任,非常优秀的中国好队友!
PSP图:
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| ·Estimate | · 估计这个任务需要多少时间 | 35 | 45 |
| Development | 开发 | ||
| ·Anlaysis | · 需求分析 (包括学习新技术) | 50 | 100 |
| ·Design Spec | · 生成设计文档 | 30 | 40 |
| ·Design Review | · 设计复审 (和同事审核设计文档) | 40 | 25 |
| ·Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 45 | 45 |
| ·Design | · 具体设计 | 60 | 140 |
| ·Coding | · 具体编码 | 120 | 160 |
| · Code Review | · 代码复审 | 60 | 40 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 140 | 170 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 60 | 90 |
| · Size Measurement | · 计算工作量 | 5 | 15 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 45 |
| 合计 | 675 | 915 |

