【原创】洛谷 LUOGU P3366 【模板】最小生成树
P3366 【模板】最小生成树
题目描述
如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出orz
输入输出格式
输入格式：第一行包含两个整数N、M，表示该图共有N个结点和M条无向边。（N<=5000，M<=200000）
接下来M行每行包含三个整数Xi、Yi、Zi，表示有一条长度为Zi的无向边连接结点Xi、Yi
输出格式：输出包含一个数，即最小生成树的各边的长度之和；如果该图不连通则输出orz
输入输出样例
输入样例#1：
4 5 1 2 2 1 3 2 1 4 3 2 3 4 3 4 3
输出样例#1：
7
说明
时空限制：1000ms,128M
数据规模：
对于20%的数据：N<=5，M<=20
对于40%的数据：N<=50，M<=2500
对于70%的数据：N<=500，M<=10000
对于100%的数据：N<=5000，M<=200000
样例解释：
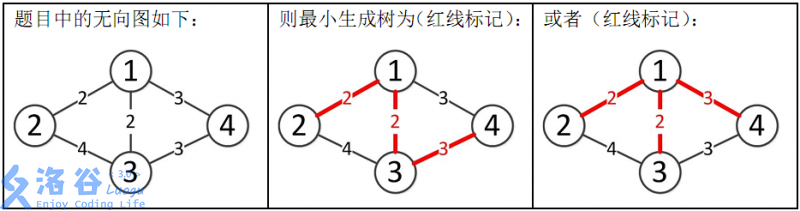
所以最小生成树的总边权为2+2+3=7
练习最小生成树，用了mhy12345大神的风格写了Kruskal算法。
Kruskal的思路：（贪心）
将边集按权值排序，
用并查集维护，从小到大连边，
这样就能保证所有环的最大边一定不被连上，
计算已加节点cnt，当cnt==n-1时即生成完毕。
若边集遍历完但cnt<n-1则图不连通。
时间复杂度即为排序复杂度，一般为O(ElogE)。
代码如下：
1 // LUOGU 3366 【模板】最小生成树 2 // 2017.7.21 12:55 3 #include<cstdio> 4 #include<cstdlib> 5 #include<cstring> 6 #include<iostream> 7 #include<string> 8 #include<algorithm> 9 #define MAXV 5010 10 #define MAXE 200010 11 using namespace std; 12 struct tEdge{ 13 int u,v,w; 14 }E[MAXE]; 15 int n,m,ans=0,cnt=0; 16 int uf[MAXV]; 17 bool cmp(const tEdge E1,const tEdge E2){ 18 return E1.w<E2.w; 19 } 20 int getfather(int v){ 21 return (uf[v]==v)?v:uf[v]=getfather(uf[v]); 22 } 23 bool Union(tEdge E){ 24 if(getfather(E.u)!=getfather(E.v)){ 25 uf[getfather(E.u)]=getfather(E.v); 26 return 1; 27 } 28 return 0; 29 } 30 int main(){ 31 scanf("%d%d",&n,&m); 32 for(int i=1;i<=m;i++) 33 scanf("%d%d%d",&E[i].u,&E[i].v,&E[i].w); 34 sort(E+1,E+m+1,cmp); 35 for(int i=1;i<=n;i++)uf[i]=i; 36 for(int i=1;i<=m;i++) 37 if(Union(E[i])){ 38 ans+=E[i].w,cnt++; 39 if(cnt==n-1)break; 40 } 41 if(cnt==n-1)printf("%d\n",ans); 42 else printf("orz\n"); 43 return 0; 44 }
