（原+译）常见的梯度下降算法

转载请注明出处：

http://www.cnblogs.com/darkknightzh/p/5785137.html

翻译网址：

http://sebastianruder.com/optimizing-gradient-descent/index.html#fn:2

参考网址：

http://blog.csdn.net/luo123n/article/details/48239963

对于凸优化问题，需要计算损失函数$L(\theta )$的极小值（最小值）。由于梯度是函数上升最快的方向，因而梯度下降算法在更新参数$\theta $的梯度时，均是减去参数的梯度。下面的$\eta $为学习率。

下面的均为一阶的梯度下降算法，二阶的由于要计算Hessian矩阵，计算量较大，因而原网址未介绍。

1. 批量梯度下降算法（batch gradient descent，BGD）

BGD在整个训练集上面计算损失函数关于参数$\theta $的梯度：

$\theta =\theta -\eta \centerdot {{\nabla }_{\theta }}J(\theta )$

由于每次更新$\theta $时均需要在整个训练集上面计算梯度，因而BGD算法比较慢，且BGD算法无法处理数据太多而无法一次性存储在内存中的情况。另外，BGD算法无法在线更新模型。

目前深度学习库能自动且有效的计算梯度，因而如果自己手动推导梯度，最好进行梯度检查。参见http://cs231n.github.io/neural-networks-3/

对于凸优化问题，BGD会收敛到全局最小值；对于非凸优化问题，BGD会收敛到局部最小值。

2. 随机梯度下降算法（stochastic gradient descent，SGD）

SGD每次选择一个训练样本对$({{x}^{(i)}},{{y}^{(i)}})$来更新参数$\theta $：

$\theta =\theta -\eta \centerdot {{\nabla }_{\theta }}J(\theta ;{{x}^{(i)}},{{y}^{(i)}})$

由于SGD每次只通过一个训练样本对来更新参数，因而比BGD快很多，也可以用于在线学习。但是SGD更新参数时很容易出现波动，因而方差很高。但是这种波动也能让SGD跳出当前的局部极小值，调到另一个更好的极小值处。当逐渐降低学习率时，SGD和BGD一样，对于非凸问题，会收敛到局部极小值；对于凸问题会收敛到全局极小值。

注意，在使用SGD时，需要对样本进行随机化处理。

3. 小批量梯度下降算法（mini-batch gradient descent，MBGD）

MBGD结合了BGD和SGD的优点，每次使用部分训练样本更新$\theta $（感觉上很多论文的SGD实际上指的是MBGD）。如训练集共N个样本，每次使用n个样本，则batch总数为N/n（假设其为整数）。第i次更新时，使用一个batch中的n个样本（上面的公式为参考网址中的，感觉不正确，下面的为自己改的）：

$\theta =\theta -\eta \centerdot {{\nabla }_{\theta }}J(\theta ;{{x}^{(i:i+n)}},{{y}^{(i:i+n)}})$

$\theta =\theta -\eta \centerdot {{\nabla }_{\theta }}J(\theta ;{{x}^{((n-1)\times i+1:n\times i)}},{{y}^{((n-1)\times i+1:n\times i)}})$

当训练数据集比较大时，利用整个训练数据来计算梯度对硬件要求比较大，如内存，CPU等，使用MBGD可以降低对硬件的要去。另外，MBGD可以降低参数$\theta $的方差，从而更快的收敛。可以使用深度学习库中高度优化的矩阵运算来更有效地计算mini-batch的梯度。实际使用中mini-batch的大小为50到250之间，但是可以根据需要进行调整。

 

上面的这三种固定学习率的梯度下降算法有其弊端：学习率太低时收敛太慢，学习率太高又可能到时损失函数在极小值处波动甚至是发散。

另一方面，SGD不易处理鞍点处的梯度。由于鞍点周围的误差相同，梯度在所有方向都接近于0，导致SGD很难脱离鞍点。

4. 动量（momentum）

由于SGD（指上面的三种方法）的参数更新完全依赖于当前的batch，容易出现震荡现象，动量通过将当前时刻的梯度与前一时刻的梯度按照一定的比例进行加权，使得当前的更新方向包括当前梯度的方向与之前时刻梯度的方向，来增加更新的稳定性，同时抑制SGD的震荡现象。

${{v}_{t}}=\gamma {{v}_{t-1}}+\eta \centerdot {{\nabla }_{\theta }}J(\theta )$

$\theta =\theta -{{v}_{t}}$

动量的系数$\gamma $表示保留原来方向的程度，通常设置为0.9左右。

当梯度指向收敛方向时，动量加快更新速度；当梯度改变方向时，动量降低更新速度。从而在保证收敛更快的同时，减弱震荡现象（暂时没想明白，不知道公式是否正确）。

动量的论文：Qian, N. (1999). On the momentum term in gradient descent learning algorithms. Neural Networks : The Official Journal of the International Neural Network Society, 12(1), 145–151. http://doi.org/10.1016/S0893-6080(98)00116-6

5. Nesterov accelerated gradient（NAG）

相比于momentum，NAG更智能，其包含一个将要去哪里的指示，因而在曲面上升时，能够降低更新速度。

使用momentum时，通过动量部分$\gamma {{v}_{t-1}}$来更新参数$\theta $，从而$\theta -\gamma {{v}_{t-1}}$给出了参数下一个近似位置。因而通过下一个近似位置来进行更新：

${{v}_{t}}=\gamma {{v}_{t-1}}+\eta \centerdot {{\nabla }_{\theta }}J(\theta -\gamma {{v}_{t-1}})$

$\theta =\theta -{{v}_{t}}$

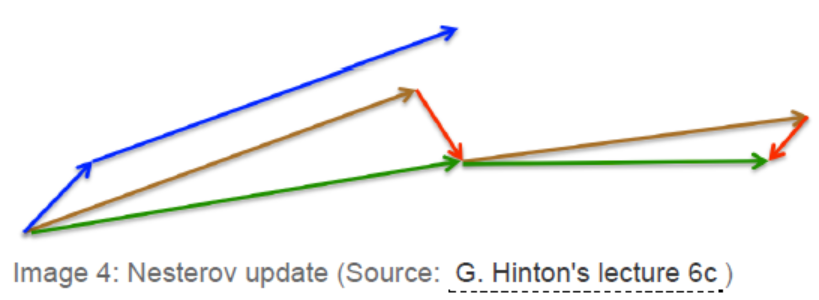
动量的系数$\gamma $通常设置为0.9左右。动量的方法首先计算当前梯度（下图中短的蓝色向量），之后通过之前梯度及当前梯度进行参数更新（长的蓝色向量）。NAG则通过之前梯度及当前梯度进行参数更新（棕色向量），并计算此时梯度（红色向量），并使用此时的梯度修正最终的更新方向（绿色向量）。NAG可以避免更新过猛，在RNNs中可以明显的提升性能。

NAG的论文：Nesterov, Y. (1983). A method for unconstrained convex minimization problem with the rate of convergence o(1/k2). Doklady ANSSSR (translated as Soviet.Math.Docl.), vol. 269, pp. 543– 547.

6. Adagrad

上面的方法在参数更新过程中，使用了固定的学习率。Adagrad自适应地为各个参数分配不同的学习率：对于不常见的参数可以进行大幅度的调整，对于常见参数则进行小幅度的微调（此处用“不常见”和“常见”不太好）。因而适用于处理稀疏数据。对于当前需要更新的参数${{\theta }_{i}}$在某时刻t：

${{\theta }_{t+1,i}}={{\theta }_{t,i}}-\frac{\eta }{\sqrt{{{G}_{t,ii}}+\varepsilon }}\centerdot {{g}_{t,i}}$

${{G}_{t}}\in {{R}^{d\times d}}$为一个对角矩阵，对角线上的值为$\theta $的梯度到当前时刻的平方和。$\varepsilon $通常为1e-8，为了保证分母非0。如果不使用开方的话，该算法性能会差很多。

Adagrad算法参数更新的矩阵形式如下：

${{\theta }_{t+1}}={{\theta }_{t}}-\frac{\eta }{\sqrt{{{G}_{t}}+\varepsilon }}\odot {{g}_{t}}$

$\odot $为矩阵对应元素相乘。该算法优点是自适应的调整学习率。一般初始学习率设置为0.01。

Adagrad的论文：Duchi, J., Hazan, E., & Singer, Y. (2011). Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. Journal of Machine Learning Research, 12, 2121–2159. Retrieved from http://jmlr.org/papers/v12/duchi11a.html 

该算法的缺点是，分母中需要计算每个参数梯度的累计平方和，由于每次均累加一个正数，训练阶段累积和会持续增加，导致训练后期的学习率非常小，以至更新时不能从当前的梯度获取任何有用信息（另外，更新参数时，左右两边的单位不统一）。下面的算法可以解决这个问题。

7. Adadelta

Adadelta对Adagrad进行了改进，不是不限次数的累加梯度，而是将之前梯度累加的次数限定为离当前时刻最近的w次。该算法并未存储之前w个时刻的梯度的平方，而是通过之前时刻梯度平方的平均来计算。当前梯度的平方和为上一次梯度的平方和与当前梯度平方的加权之和（不太懂为何这样可以）。

$E{{\left[ {{g}^{2}} \right]}_{t}}=\gamma E{{\left[ {{g}^{2}} \right]}_{t-1}}+(1-\gamma )g_{t}^{2}$

$\gamma $和动量项类似，为衰减系数，也设置为0.9左右。通过这个衰减系数，我们令每一个时刻的${{g}_{t}}$随着时间按照ρ指数衰减，这样就相当于我们仅使用离当前时刻比较近的${{g}_{t}}$信息，从而使得很长时间之后，参数仍然可以得到更新（参考网址2）。此时更新公式如下：

$\Delta {{\theta }_{t}}=-\frac{\eta }{\sqrt{E{{\left[ {{g}^{2}} \right]}_{t}}+\varepsilon }}{{g}_{t}}$

由于分母是均方根误差（RMS error），因而可以写为下式：

$\Delta {{\theta }_{t}}=-\frac{\eta }{RMS{{\left[ g \right]}_{t}}}$    感觉该公式有问题

将上面公式改成关于${{\theta }_{t}}$的：

$E{{\left[ \Delta {{\theta }^{2}} \right]}_{t}}=\gamma E{{\left[ \Delta {{\theta }^{2}} \right]}_{t-1}}+(1-\gamma )\Delta \theta _{t}^{2}$

$RMS{{\left[ \Delta \theta  \right]}_{t}}=\sqrt{E{{\left[ \Delta {{\theta }^{2}} \right]}_{t}}+\varepsilon }$

由于$RMS{{\left[ \Delta \theta  \right]}_{t}}$未知，使用之前时刻的RMS值代替。最终的Adadelta更新公式为：

$\Delta {{\theta }_{t}}=-\frac{RMS{{\left[ \Delta \theta  \right]}_{t-1}}}{RMS{{\left[ g \right]}_{t}}}{{g}_{t}}$

${{\theta }_{t+1}}={{\theta }_{t}}+\Delta {{\theta }_{t}}$

使用Adadelta，由于随着参数更新，学习率的影响慢慢消失，因而都不需要设置默认的学习率。

Adadelta的论文：Zeiler, M. D. (2012). ADADELTA: An Adaptive Learning Rate Method. Retrieved from http://arxiv.org/abs/1212.5701

8. RMSprop

RMSprop未发表，但是也是自适应学习率的算法，由Geoff Hinton提出（http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf）。该算法实际上和Adadelta类似：

$E{{\left[ {{g}^{2}} \right]}_{t}}=0.9E{{\left[ {{g}^{2}} \right]}_{t-1}}+0.1g_{t}^{2}$

${{\theta }_{t+1}}={{\theta }_{t}}-\frac{\eta }{\sqrt{E{{\left[ {{g}^{2}} \right]}_{t}}+\varepsilon }}{{g}_{t}}$

默认的学习率是$\eta $=0.001。

9. Adaptive Moment Estimation（Adam）

Adam也可以自适应的计算各参数的学习率。Adam不仅计算指数衰减梯度平方的二阶矩的估计${{v}_{t}}$，如Adadelta与RMSprop，其还计算指数衰减梯度的一阶矩的估计${{m}_{t}}$，类似于动量。

${{m}_{t}}={{\beta }_{1}}{{m}_{t-1}}+(1-{{\beta }_{1}}){{g}_{t}}$

${{v}_{t}}={{\beta }_{2}}{{v}_{t-1}}+(1-{{\beta }_{2}})g_{t}^{2}$

其中${{m}_{t}}$为一阶矩的估计（均值），初始化为0向量；${{v}_{t}}$为二阶矩的估计（方差），初始化为0向量。Adam的作者发现当衰减率（decay rate）很小时（${{\beta }_{1}}$和${{\beta }_{2}}$接近于1），${{m}_{t}}$和${{v}_{t}}$最终都趋于0。因而Adam算法最终对一阶矩和二阶矩进行校正（${{\beta }_{1}}$和${{\beta }_{2}}$的上标t代表t次方）：

${{\hat{m}}_{t}}=\frac{{{m}_{t}}}{1-\beta _{1}^{t}}$

${{\hat{v}}_{t}}=\frac{{{v}_{t}}}{1-\beta _{2}^{t}}$

最终Adam的更新规则为：

${{\theta }_{t+1}}={{\theta }_{t}}-\frac{\eta }{\sqrt{{{{\hat{v}}}_{t}}}+\varepsilon }{{\hat{m}}_{t}}$

默认情况下，${{\beta }_{1}}=0.9$，${{\beta }_{2}}=0.99$，$\varepsilon ={{10}^{-8}}$，$\eta =0.001$。

Adam的论文：Kingma, D. P., & Ba, J. L. (2015). Adam: a Method for Stochastic Optimization. International Conference on Learning Representations, 1–13.

 

10. 算法的选择

如果数据比较稀疏，最好使用自适应学习率的算法。如果不清楚具体使用哪个的话，使用Adam就可以了。