OO第一单元总结

 第一次作业

 

 1.项目结构

本次类主要分为3个，main类，用于预处理的Preprocess类和用于拆解，求导并打印表达式的PowFunc类。

第一次的作业比较简单，不需要判断Wrong Format，只需要将表达式预处理成方便求导的形式然后求导就可以了。预处理过程主要分为以下几步：

　　1.去除空格

　　2.将多个连续的正负号变为一个

　　3.补充缺失的系数（+1，-1等）

　　4.补充缺失的指数**1。

2.代码复杂度分析

 

 

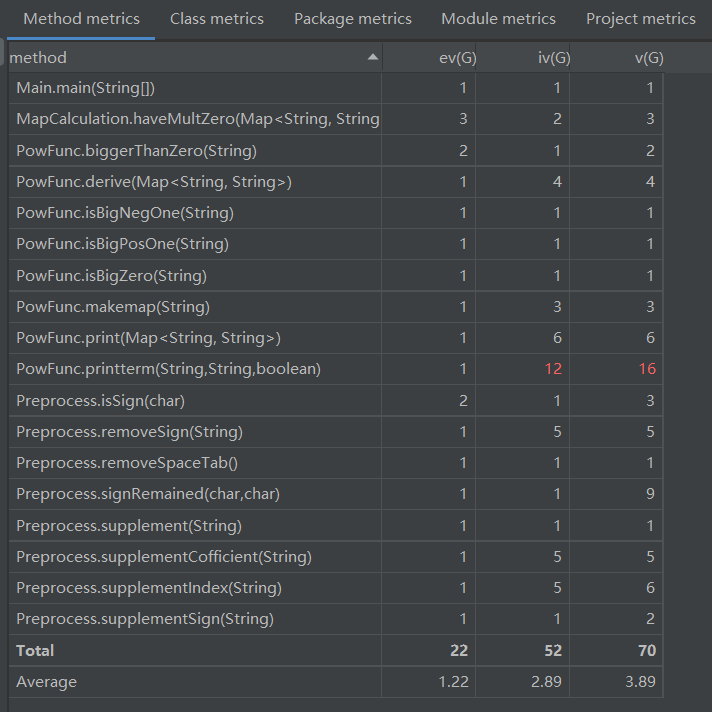
 由上图可以发现方法的复杂度整体都不高，但是printterm函数的复杂度明显很高。导致printterm复杂度升高的部分如下图所示：

 

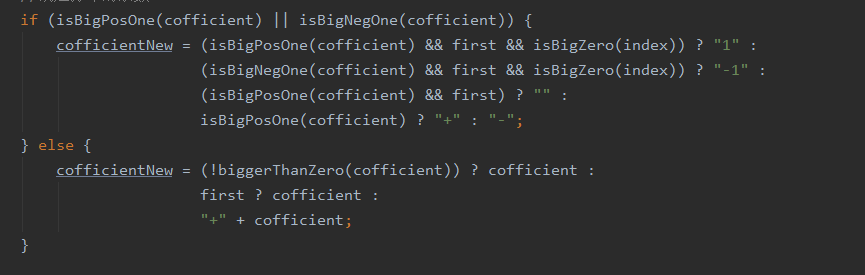
 圈复杂度大说明程序代码可能质量低且难于测试和维护。确实在写这块代码课下自己测试的时候这里发现了不少问题。这也启示了我以后写完代码后可以用代码复杂度分析工具分析模块的复杂性，针对复杂的模块要多设立测试点测试。根据帕累托原则，20%的模块中可能含有系统80%的bug，所以测得bug的模块往往含有更多的bug，需要多加测试。

3.bug分析

（1）合并同类项

　　第一次作业中我在合并同类项的时候出现了bug，因为我根据每一项建立了一个HashMap，Key为指数，Value为系数。由于我在合并同类项时简单地让HashMap判断是否contains Key的字符串，然而这导致了一个严重的问题就是形如指数为“2”和“+002”的两项并不会被合并，因为它们字符串并不相同，然而实际上指数是相等的。所以一个方法是先把指数转为BigInteger再比较，这样的话由于BigInterger兼容性较好，可以自动把“+0002”这种既带正负号又带前导0的数字转化为标准格式。之后比较字符串时就不会出现这种问题。

（2）一些特殊的情况

　　比如-x+x，因为有的同学优化时项为0的不输出所以最后的结果是没有输出，导致bug。

（3）map中遍历时删除操作的正确方法

for (Iterator<Map.Entry<String,String>> it = map.entrySet().iterator(); it.hasNext();) {
    Map.Entry<String,String> item = it.next();
    String cofficient = item.getValue();
    if (cofficient.equals("0")) {
                    it.remove();
    }
}
                

　　而以下两种Map的遍历方法都不适合做删除操作：

HashMap<String,String> map = new HashMap<>();
Set<String> key = map.keySet();
for (String s : key) {
    //do something
    map.remove(s);
}

HashMap<String,String> map1 = new HashMap<>();
Set<Map.Entry<String,String>> entrySet = map1.entrySet();
for(Map.Entry<String,String> entry : entrySet) {
    //do something
    map1.remove(entry.getKey());
}

　　第一次作业中互测时有同学采用了不正确的遍历方法删除之后就会出现bug。

（4）正则表达式使用注意事项

• 正则表达式不宜写的很长，如果写的比较则应该分成多条来写，增强代码可读性同时方便自己debug,正则表达式debug的方法可采用下文中的第（5）条，使用check RegExp来检查。

有的同学正则表达式只写成了一条，写的很长，就很容易出bug，互测当中我看到了这样写的同学就去测他的正则表达式，果然发现了bug。

• 前2次作业中由于没有空白引起的Wrong Format，所以我把所有空格去掉后再匹配格式，这样就可以适当缩减正则表达式的长度降低出错几率。
• 正则表达式需要留神爆栈问题。虽然在我们这届的指导书中往往对输入字符串的长度有较强的限制一般不容易出现爆栈的现象，然而在往届同学的博客中提到确实存在有的同学在互测中由于正则表达式爆栈而出错的情况。
• 为了防止正则表达式爆栈，可以采取以下策略：
• 懒惰匹配
• 了解自动机原理后做原理层面的优化（很复杂）

（5）小技巧1：BigInteger中自带的固定值

BigInteger中有三个基本常理：

BigInteger.ZERO
BigInteger.ONE
BigInteger.TEN

　　-1可以采用BigInteger.ONE.negate()以赋值。

（6）使用intellij自带的check RegExp来方便地检测正则表达式是否正确。

 

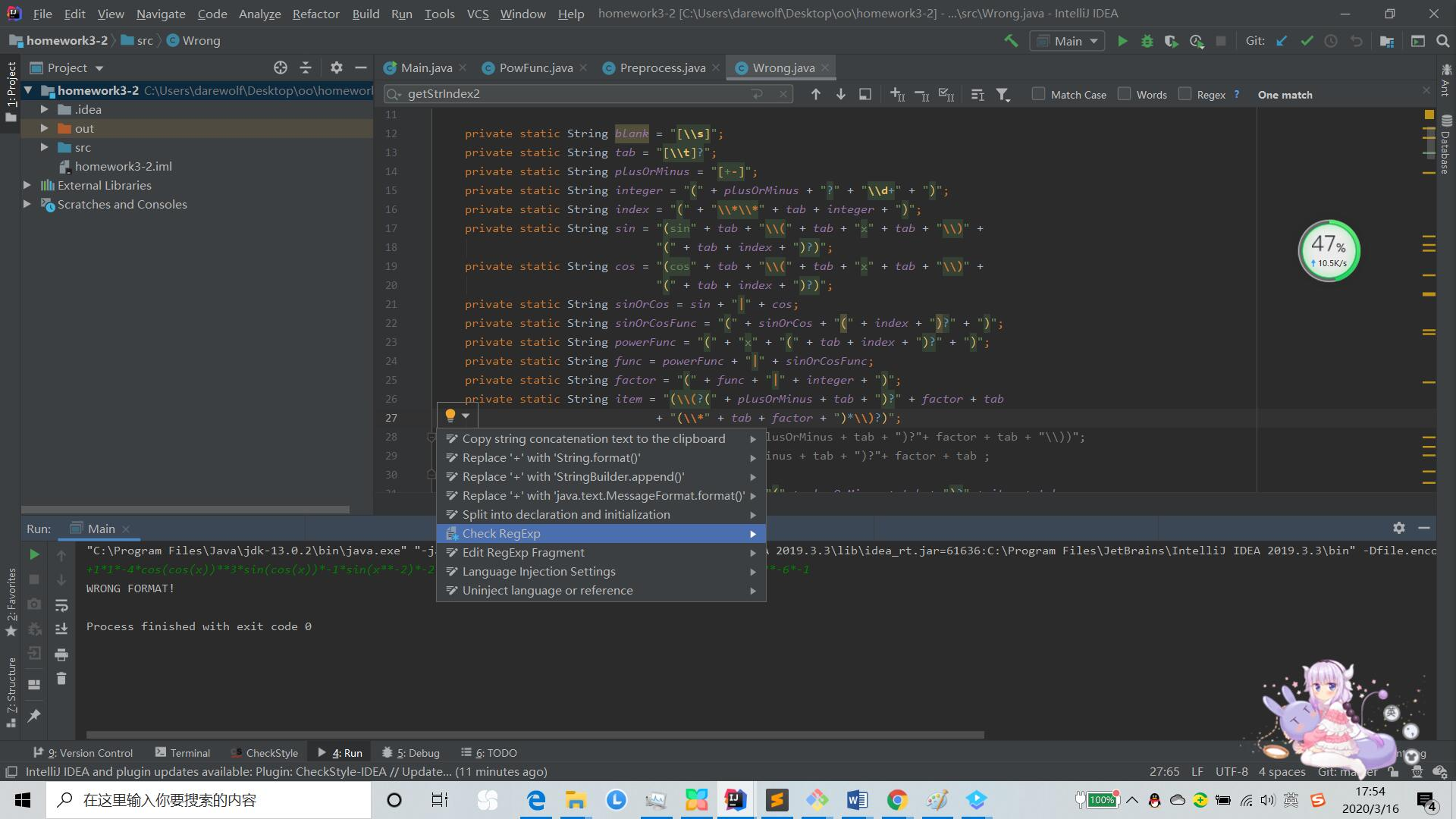
 在正则表达式“”中的任意一处点击一下，就可以在左侧的下拉菜单中选取check RegExp选项，然后可以在弹出框中输入字符串，会显示字符串是否匹配正则表达式。

字符串如果匹配则如下图所示：

 

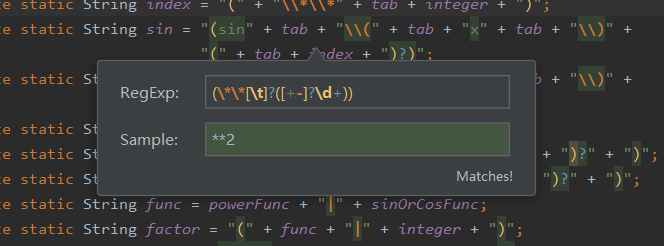
 字符串如果不匹配则如下图所示：

 

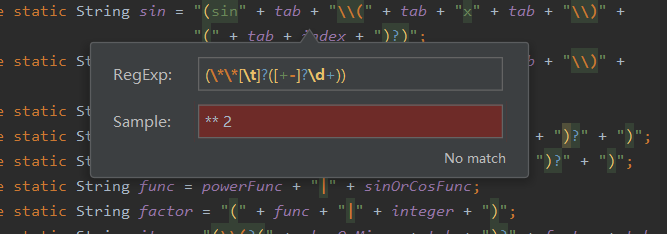
 第二次作业

 1.项目结构

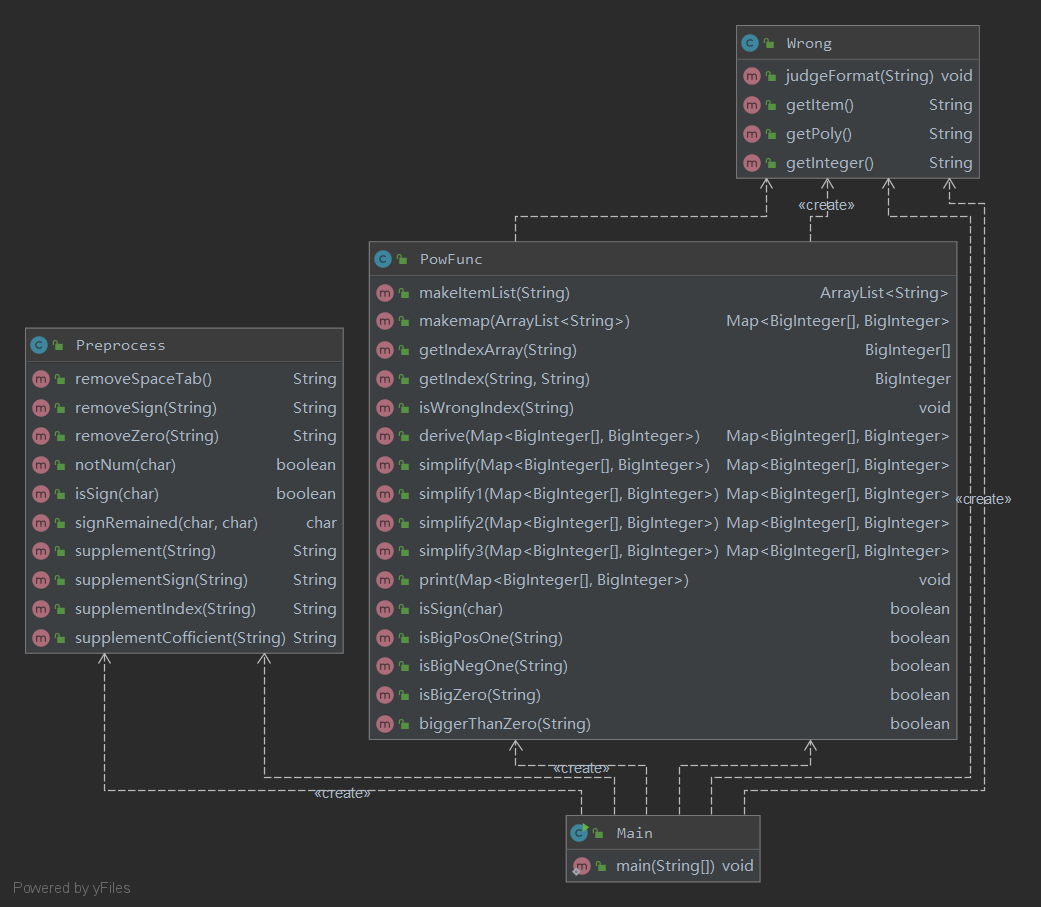
 　　第二次作业引入一个新模块Wrong，主要用来判断是否Wrong Format。由于第二次作业正则表达式不会出现嵌套的现象，故根据指导书写出所有的正则表达式便可轻松地判断表达式是否符合格式。

 2.代码复杂度分析

 

 

 

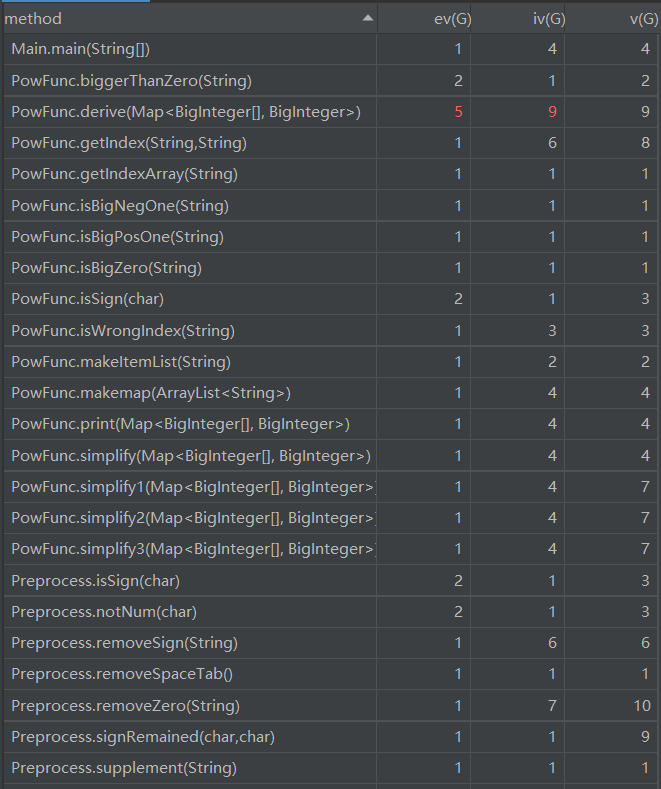
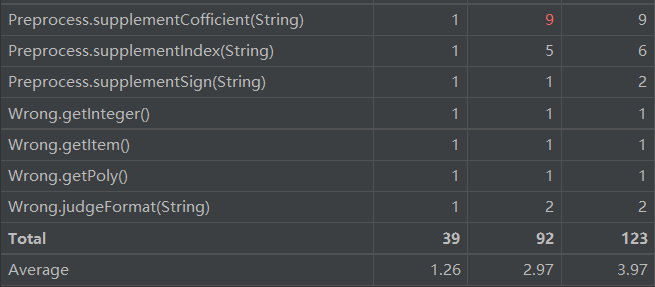
　　 由上图可知，derive模块的复制程度较高，应继续做类的拆分。derive模块核心代码如下：

if (coff.compareTo(bigZero) == 0) {
                continue;
            } else {
                for (int i = 0;i <= 2;i++) {
                    System.arraycopy(indexArr,0,indexArrNew,0,3);
                    if (indexArr[i].compareTo(bigZero) == 0) {
                        continue;
                    } else if (i == 0) {
                        coffNew = indexArr[i].multiply(coff);
                        indexArrNew[i] = indexArr[i].subtract(bigOne);
                    } else if (i == 1) {
                        coffNew = indexArr[i].multiply(coff);
                        indexArrNew[i] = indexArr[i].subtract(bigOne);
                        indexArrNew[2] = indexArr[2].add(bigOne);
                    } else if (i == 2) {
                        coffNew = indexArr[i].multiply(coff).multiply(bigNegOne);
                        indexArrNew[i] = indexArr[i].subtract(bigOne);
                        indexArrNew[1] = indexArr[1].add(bigOne);
                    }
                    //放入map

                    System.arraycopy(indexArrNew,0,indexArrNewPut[bigArri],0,3);
                    if (mapRet.containsKey(indexArrNewPut[bigArri])) {
                        mapRet.put(indexArrNewPut[bigArri],
                                mapRet.get(indexArrNewPut[bigArri]).add(coffNew));
                    } else {
                        mapRet.put(indexArrNewPut[bigArri],coffNew);
                    }
                    bigArri += 1;
                }

 

 　　这里可以采用工厂模式，建立一个求导后项的系数和指数的值的工厂。传入原系数和指数数组的HashMap和循环变量i，传回求导之后各项组成的HashMap。这样就可以大大降低derive模块的复杂度，可读性更强。

3.bug分析

（1）带有前导0的指数求导依然是易错点

本次我在公测和互测中都未被hack，hack了别人的两个bug：

-+x*x**2*x**+00002*-4*sin(x)*sin(x)**2*sin(x)**-0002

x*sin(x)**0002*sin(x)**-0001*sin(x)**-1

　　这说明在第二次作业中带有前导0的复杂指数化简依然是一个容易出错的问题。

　　下面我想说一个在课下让我“命悬一线”的问题

（2）非常不建议把数组类型作为HashMap的Key。

　　在做第二次作业时在求导方面我并没有考虑很好的扩展性，考虑了一种“投机取巧”的办法，即所有的项都有一个通用的形式a*x**b*sin(x)**c*cos(x)**d，每一项求导之前与求导之后的格式都为a*x**b*sin(x)**c*cos(x)**d。所以我建了一个存储项的HashMap，Key为int[3]的数组，分别存储x,sin(x)和cos(x)的指数，即[b,c,d]，Value为前面的系数，即为a。我最初的想法是这样建的话有利于合并同类项，因为不能合并同类项的两项之间[b1,c1,d1]和[b2,c2,d2]并不相同。

　　然而当我使用map.contains(int[])的时候却发现并没有像我想的那样成功合并同类项。原因在与map.contains()比较两个Key的时候的原理是采用.equals()方法，然而这个方法并不能比较两个含有相同值的数组，所以map.contains()无法通过正常的方法来识别是否含有一样的数组。如下方的代码会输出false:

 

　　　　 int [] a = {1,2};
　　　　　int [] b = {1,2};
        boolean c=a.equals(b);
        System.out.println(c);

 

第三次作业

1.项目结构

（1）判断格式的非递归实现

• 指导书上给的正则表达式会需要递归调用，然而java的正则表达式并不能像有的语言一样可以递归调用（不知道为什么不加这个功能）
• 下图即为指导书中有关递归调用正则表达式的过程

 

• 经过仔细思考可以换一种非递归理解方式，即因子可以带括号（也就成了表达式因子），也可以不带（其他因子）。
• 项可以是一个因子，表达式也可以是一个因子。
• 所以项两侧可有括号可没有，表达式也是如此。
• 故代码可如下所示：

private static String factor = "(" + func + "|" + integer + ")";
private static String item = "(\\(?(" + plusOrMinus + tab + ")?" + factor + tab
                                + "(\\*" + tab + factor + ")*\\)?)";
private static String poly = "\\(?" + tab + "(" + plusOrMinus + tab + ")?" + item + tab+ "([+-]" + tab + item + tab + ")*" + "\\)?";

 

经测应该无误，通过了所有自己和公测的Wrong Format测试点 。

• 之后判断指数大小是否符合范围
• 通过栈判断表达式的括号是否匹配（有的同学没有考虑）

 

（2）求导过程的非递归实现

　　其中我想重点讲一下我的求导方面的架构设计。讨论区中以及绝大部分人的方法基本都离不开递归，或者构建了表达式树然后再递归。然而这样导致一个问题就是递归层数如果深的话就有可能导致爆栈，如：

 ((((((((((((((((((((((((x)))))))))))))))))))))))))))。所以你讨论区里很多同学提出可以拆除没有意义的括号，我想到的情形主要有以下几种：

• ((((((((((((((((((((((((x)))))))))))))))))))))))))))，因子两边嵌套数层括号但其实并没有什么意义，故如果两层括号紧密相连，如(())，就可以拆除其中的一层括号。
• (x+(x+(x+……，括号外侧由正号或者负号连接，括号无用，可直接去除。
• (x*(x*(x+……，虽然括号外侧由乘号连接，但是括号内部是一项，即没有项与项之间的正负号，则括号无用，可以直接去除。

　　然而有一些项是不能通过这种方式来去除括号的，比如sin(sin(sin……sin(x)……），最多可以有11层。虽然数据限制或许导致并不会爆栈，然而这个问题并没有得到真正解决，即递归层数稍一变多就会爆栈。

　　所以我觉得采取一种非递归的算法，虽然思考难度比递归大不少但是可以一劳永逸地解决问题。递归其实是从最外层的括号开始求导，如果内层函数含有括号则继续递归。而非递归方法则与之相反，先求出最内层括号的导数值，然后一层一层向外求导。这个题目可以采取非递归的算法的本质原因是你可以根据表达式预知括号的层数即分布。也就是说根据表达式可以先建立一个字符数组，将表达式中所有的括号放入其中。然后就可以得知括号的层数，之后就可以先把最内层的一个或多个括号内的表达式求出导数，同理向外求导直到没有括号。由于我在执行此方法时会在整个表达式外套上一层括号，故求到最外层后即为整个表达式的导数。这个方法听起来并不困难，但其实写起代码来却要解决好几个递归不需要考虑的问题，难度较大。

下面举一个简单的例子解释这个方法。比如对这个表达式进行求导：(x+1)*(x+2)，

• 第一步给外层加上括号((x+1)*(x+2))
• 第二步提取括号数组：(()())，易得括号深度为2。
• 第三步求出所有深度为2的括号内的表达式的导数，都为1.
• 第四步求出最外层括号内对应表达式中的导数。

 2.代码复杂度分析

 

 

 

 

 

 

 

 

 

 　　以上6个方法为第三次作业中所以复杂度不符合规范的方法。前两次作业分别只有1个和2个方法不符合规范，充分说明了在方法划分不合理的时候，当一个工程的代码变复杂以后，复杂的模块数目几乎以指数的速度增长，复杂的模块也导致出bug的概率大大增加。

　　其中第一张图中的四个方法全部与求导有关，这四个方法的含义分别是给因子进行求导，给一项进行求导，和对整个表达式进行求导。z这几个方法中由于使用了嵌套的if-else使得复杂度一下升高，故可以采用的工厂模式的方法，工厂生产幂函数，sin函数，cos函数的导数，然后求导方法里直接调用可以很好地降低方法的复杂度。

3.bug分析

（1）括号不匹配

　　有的同学并没考虑到括号不匹配导致WRONG  FORMAT的问题。判断括号匹配最好的方法之一是使用栈，遇到一个左括号就入栈，遇到一个右括号就出栈一个左括号。如果最后栈中括号的数目为0就说嘛括号匹配。

（2）输出格式错误

　　比如输出（表达式）**0这种答案，可行的方法是使用正则表达式将这种式子替换为1。

（3）递归爆栈

　　有的同学递归没有做任何预处理，导致((((((((((((((((((((((((x)))))))))))))))))))))))))))这种递归深度很深的表达式直接爆栈。

应用工厂模式重构

　　我觉得针对我的代码接口主要可以改为3个，预处理，求导和简化。这三步主要操作都可以分为好几部小操作，可以使用工厂模式进行实现。

　　在重构时应主要参考前文中模块的复杂度，对含有嵌套的大量if-else模块以及行数大于要求（最好不超过30行）的模块进行拆解或者使用工厂模式，比如第三次作业中的几个求导模块，都出现了if-else嵌套导致复杂度迅速上升的现象，可以用工厂模式进行解决。

　　具体到因子的求导还可以使用求导因子的接口，分别用幂函数，sin函数，cos函数求导的方法进行实现。

分析别人bug的策略

• 首先可以采用“盲测”的方法，即输入自己觉得易错的测试点，不管对方的代码结构，这种方法虽然暴力但很多时候却很有效。
• 如果遇到对方写很复杂的正则表达式则可以测试对方的正则表达式是否正确，是否会出现爆栈等现象。
• 遇到对方有比较明显的结构错误，如hashmap遍历删除元素时采用了不稳定的方法，那么就多多构造需要删除元素的数据点，很容易就测得对方的错。
• 我觉得除非对方有明显的结构错误或者不规范的地方，否则单纯看对方代码可能很难发现bug，这是采取暴力对拍可能能更快地发现bug。
• 对拍只能作为手动测试的补充，因为对拍生成的数据点随机性较强但是不一定很强，有同学反应在互测过沉中评测机对拍未发现任何bug，而手测反而发现了好几个bug。

 对比和心得体会 

 1.关于性能优化

• 保证正确性是最重要的，如果有的优化性能使程序具有很高的复杂度那么就应该放弃对应部分优化。比如第三次作业中如果细究所有的优化可以说是无穷无尽的，三角函数嵌套的表达式具体的化简甚至有专门的论文，而完全把时间全部放在优化上其实并不划算而且风险不小。我记得讨论区里有人说过有的大佬优化的结果比simplify还要简单,说明即使是工业级的函数也追求的是在不太多的函数内尽量达到最好的效果，而非必须追求数学上的极致完美，如何学长在优化时采用了蒙特卡洛的方法，虽然在数学上不一定能化简到完美，却可以用不是很复杂的代码达到较好的效果，在应用中更具有实用性。而在性能分数中事实证明只要做到一些很基本的优化：包括合并同类项，去除0项，省略系数和指数，就可以取得很好的性能成绩。

 2.关于类的拆分

• 应适当增加类的数目，使得每个类都不很复杂，如田佬和林佬等的代码中都有很多个类，每个类往往不太复杂。
• 单个方法控制最长不超过30行左右，单个类的长度尽量控制在100行左右。如果超过这个长度，就要考虑将其进行细分。
• 包（Package的使用）：设立很多个类后还可以把类根据类别放在不同的package中，使类看起来比较整齐不杂乱，同时不同包里的方法还可以采用相同的名字，这样就不用担心名字重复的问题。而我在前3次作业中简单粗暴地把所有问你件放在src里，结构并不清晰明了。
• 包的详细应用方法可参考以下资料：https://www.runoob.com/java/java-package.html
• 田佬对方法的拆分就很细致，感觉很“面向对象”，值得学习。

 3.测试数据

• 自动化评测机可以节约大量测试的时间，然而对拍只能作为手动测试的补充，因为对拍生成的数据点随机性较强但是不一定很强，有同学反应在互测过沉中评测机对拍未发现任何bug，而手测反而发现了好几个bug。这也引来了一个问题，如何有策略地生成数据达到强测的效果。其实我在计组的时候也体会到了这一点，真正随机生成的数据其实很弱，很多bug都测不出来，这时就要有策略地生成强测数据。比如我觉得在前3次作业中大部分特殊情况都与0,1，-1这几个数字有关，无论是省略还是化简部分。为了普遍性，再加入2，-2这两个值，因为在数学上可以近似认为如果2和-2都对那么3和-3以及其他不是0,1，-1的数字就很可能也对。所以就可以让表达式的系数和指数都限定在0,1，-1，2，-2范围内随机生成数据自动比对。

 4.常见集合类型用法的简要总结

• ArrayList：底层基于数组，在java中自认为基本可以代替数组使用，查询快，增删慢，线程不安全。
• LinkedList：底层基于链表，查询慢增删快，线程不安全。
• set集合相同的元素只能含有一个，有时候当需要保证相同的值只能保留一个的使用场景中很有用。比如寒假作业就有一道这样的题。
• HashSet:无序，存储顺序和取出顺序不一致。
• LinkedHashSet：存储和取出顺序一致。
• TreeSet:使用自然顺序进行排序，或者按照创建treeset时创建的Comparater排序。
• HashTable：Key和Value都不允许出现Null值。
• HashMap：随着时间的推移Map中的次序可能发生改变，NUll可以作为键。HashMap不推荐Key类型使用数组，详情请见本文第二次作业的bug分析。
• TreeMap：根据Key对节点进行排序。

 5.帕累托定律

• 20%的模块会承担程序80%的功能
• 20%的模块往往会出现程序80%的bug
• 容易出bug的20%的模块往往是最复杂的模块，故修改bug的同时也有可能引来新的bug。有研究表明，20%以上的场景中当修复复杂模块的bug时，会引入新的bug
• 启示：可以分开简单地测试一下各个模块，对测出bug的模块必须反复测试。同时为了防止修复bug的时候引入了新的bug，修复bug 的过程需要满足回归测试，即之前运行正确的数据点必须依然运行正确。Junit可以比较方便地进行回归测试，模块测试。我第一单元作业还没用过，以后尽量尝试使用。

 6.构思清楚再写代码

• 把思路甚至是比较具体的细节构思清楚之后再开始敲代码，不要急于敲代码。上学期高老师曾说过，设计代码时期耗费的时间会加倍地报答你。见过有的同学想构造表达式树但在敲代码前并没有构思清楚，导致写了一半之后觉得写不下去了出现很多bug直接重构，耽误了大量时间。

 7.杂七杂八

• 不要把事情拖到DDL，因为OO工作量大，拖到DDL是真的写不完，也见过很多同学奋斗到最后一小时（我也是其中之一）。
• 适当增加一些处理异常的语句，如try catch等，虽然对通过数据点貌似没有直接帮助，然而让自己的程序面临难以预测的各类异常时尽量不会崩溃确是软件的重要职能之一。
• 我的代码虽然也使用了一些面向对象的思想，然而还是挺不“面向对象的”，类的拆分方法的拆分不尽合理，java的现成轮子用的也不到位，在作业中为了短时间内追求正确性也没有用工厂模式来写，同时异常处理什么的也没有做，可以说缺陷确实特别多，同时分数也比较不理想，希望我第二单元可以做的更好。