南昌航空大学 软件学院 pta java 第一阶段总结
嗨嗨嗨
到了每月一次的总结时间了
主要是总结前三次
具体代码在另外几篇博客里
本博客更多的对一些重要的题目做一个讲解和总结

目录
代码链接
前言
三次题目都完(也)美(许)写完了,java作业治好了我的精神内耗?

对于森林小精灵laster、大佬jc等等等等人秒杀三期作业的行为我只能orz.but,他们的强大并不影响我老老实实敲代码,我绝对不当压力小子,坚持稳扎稳打,也希望大家也能耐住性子打代码,不要网上随便找到一串别人的代码就狠狠偷。接下来我会以题量、知识点和难度三个方面对三次作业的总体水平进行一个简单评价。
题量
题量方面,作业一为7题,作业二三为3题,虽然作业一题量更大但实际上是三的题量更大一些hhhh,在第三次作业的题目里,有很多的case,而那些case要比题目一中的题目要复杂的多,题量最少的是第二次作业。
知识点
知识点方面,第一二次作业主要是语法的学习,第二次还有于正则表达式的学习,但是用面向过程的方法也能很好解决,第三次作业主要是对面向对象方法的学习,如果方法和类封装的不好会做的很吃力。
难度
难度方面,最难的肯定是第三次,然后是第一次,最后是第二次。第三次的难度在于早已忘了的的数学知识、复杂的判断,还有精度控制(还有正则表达式hhhh)。第一次的难度更多在于语法的不熟悉,很多人都是第一次用java,而且java的语法扩展上有很多与c不一样的地方,所以难点更多在于对新鲜事物的学习与使用,并且第一次整整有七题,一题一题敲还是要花很长时间的,另外还有一些精度的坑hhhh,真的很浪费时间。

第二次和另外两次比起来就好很多,相对来说难度就没那么大,题量或者是题目难度来说,都不是很高,唯一可以体现含金量的正则表达式过程,都被我用if else的分支结构给解决了。
设计与分析
个人认为,代码的设计构造要比过题思路要重要的多,要是一些方法没封装起来,会让人绕晕,而且代码可读性巨差(有幸看过一些学弟学妹的代码,乍一眼巨晕hhh。他们在一坨if else中还能把代码思路理清楚真的挺厉害的)。而我也勉勉强强做到了封装。后面我会对几个比较重要的题目进行剖析,按类按方法进行讲解和作用。
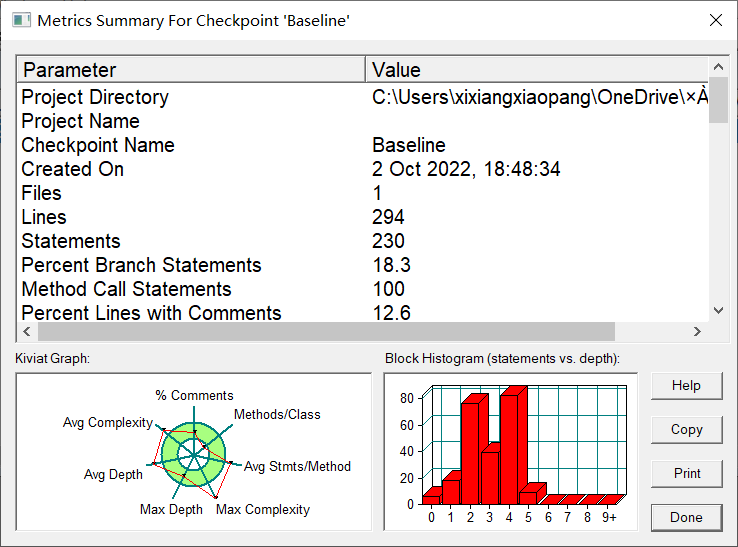
7-2 串口字符解析
很惭愧,这题我用的是面向过程的写法,只有一个类一个方法,圈复杂度有点抽象。
不急,先看题。
RS232是串口常用的通信协议,在异步通信模式下,串口可以一次发送5 ~ 8 位数据,收发双方之间没有数据发送时线路维持高电平,相当于接收方持续收到数据“1”(称为空闲位),发送方有数据发送时,会在有效数据(5~8位,具体位数由通信双方提前设置)前加上1位起始位“0”,在有效数据之后加上1位可选的奇偶校验位和1位结束位“1”。请编写程序,模拟串口接收处理程序,注:假定有效数据是8位,奇偶校验位采用奇校验。
题目的大概意思就是处理一个字符串,并从中读出一段段数据,数据是有包头包尾的,且题目设置一个数据包长度为11个字符串,看懂这些其实就很简单了。即使仅仅使用面对过程的方法也很轻松
只有一个类,没啥比较,算法简单,圈复杂度也简单。
Main
很遗憾的,只有一个main类和一个main方法,想来想去还是不想改,大概是记录自己一个学习的过程,让很多年后的我还能看看当年写的屎山hhh。
public class Main {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
String ch;
int flag=1;
ch = input.next();
if(ch.length()<11){
System.out.printf("null data");
return;
}
A:for(int i=0;i<ch.length();i++){
if(ch.charAt(i)=='0'&&ch.length()-i>10){
System.out.printf("%d:",flag++);
if(ch.charAt(i+10)!='1'){
System.out.printf("validate error\n");
i+=10;
continue ;
}
int f=0;
for(int j=i+1;j<i+9;j++)
if(ch.charAt(j)=='1')
f++;
if(((f&1)==0&&ch.charAt(i+9)!='1')||((f&1)==1&&ch.charAt(i+9)!='0')){
System.out.printf("parity check error\n");
i+=10;
continue ;
}
for(int j=i+1;j<i+9;j++)
System.out.printf("%c",ch.charAt(j));
i+=10;
System.out.printf("\n");
}
}
if(flag==1){
System.out.printf("null data");
return;
}
}
}
7-1 点线形系列1-计算两点之间的距离
题目简洁明了,就是要给你一串字符,问你其中包含的两个点的距离。
难点在于正则表达式hhhh,搞了我巨久,好在最后彻底学会了,但是后面的正则表达式还是改了点,光用这个正则表达式后面题目的case过不去。其他没啥难度,算是一个顺承的过程,这个题目写的代码后面还能用。
圈复杂度开始抽象起来了hhh。
1.Point
属于点的类,包含有两点距离计算。
class Point {//点的类
double x = 0 , y = 0 ;
double DistanceCalculation(Point b) {
return Math.sqrt((this.x-b.x)*(this.x-b.x)+(this.y-b.y)*(this.y-b.y));
}//返回两点距离
}
2.PointTaking
本来是作为字符输入和坐标剥离的,但是面向过程之魂燃烧,就开始处理起来了,是实际的主函数。
class PointTaking {
String ch;
double Solve() {
Point a = new Point();
int pos = 0;
Point b = new Point();
// String[]
String[] c = this.ch.split(" ");//将字符串以空格分割
for(String i:c) {//对分割的字符串遍历
String[] d = i.split(",");
for(String j:d) {
// System.out.printf(j+"\n");
if(!j.matches("^[+-]?(([0-9][1-9]*\\.\\d+)|(0\\.\\d+)|([0-9][1-9]*))$"))//正则表达式判断是否合法
return -1;//返回输入错误
if(pos==0)//按位读入坐标x1,y1,x2,y2
a.x =Double.parseDouble(j);
else if(pos == 1)
a.y = Double.parseDouble(j);
else if(pos == 2)
b.x=Double.parseDouble(j);
else
b.y =Double.parseDouble(j);
pos++;
}
}
if(c.length!=2)
return -2;//返回错误点数量
return a.DistanceCalculation(b);
}
}
7-2 点线形系列2-线的计算
从这题开始开启困难模式了,咱来看看要求。
1:输入两点坐标,计算斜率,若线条垂直于X轴,输出"Slope does not exist"。
2:输入三个点坐标,输出第一个点与另外两点连线的垂直距离。
3:输入三个点坐标,判断三个点是否在一条线上,输出true或者false。
4:输入四个点坐标,判断前两个点所构成的直线与后两点构成的直线是否平行,输出true或者false.
5:输入四个点坐标,计算输出前两个点所构成的直线与后两点构成的直线的交点坐标,x、y坐标之间以英文分隔",",并输出交叉点是否在两条线段之内(不含四个端点)的判断结果(true/false),判断结果与坐标之间以一个英文空格分隔。若两条线平行,没有交叉点,则输出"is parallel lines,have no intersection point"。
好家伙,一题更比六题强。

蛋黄猫看完都累趴了
咱们来梳理一下几个要求:1、判断垂直;2、判断点到直线距离;3、判断三点是否在一条直线;4、判断两直线是否平行;5、计算交叉点。
梳理完其实就很明了了,我按case给大家讲解一下我的代码。
case1
首先肯定是判断斜率是否为0,即两点x坐标相等,然后直接输出斜率,斜率这块我是封装在了线的类中的,在后面我会贴上各个类。
圈复杂度高起来了。
if(pointSet[1].x==pointSet[2].x) {
System.out.printf("Slope does not exist");
return 4;
}
line.a=pointSet[1];
line.b=pointSet[2];
System.out.printf(line.slope()+"");
case2
还是和上题一样,贴上封装好的点到直线距离方法就行,方法会贴在后面。
line.a = pointSet[2];
line.b = pointSet[3];
System.out.printf(line.pointVerticalDistanc(pointSet[1])+"");
return 4;
case3
判断是否在一条直线上,直接设置1、2点一条直线,以及1、3点一条直线,判断斜率是否相等,相等就是在一条线上。
Line line2= new Line();
line2.a = line.a = pointSet[1];
line.b=pointSet[2];
line2.b = pointSet[3];
if(line2.slope()==line.slope())
return 1;
return 2;
case4
这题不能直接用封装好的斜率了,因为有精度问题,把斜率公式搬过来就a了。
Line line2= new Line();
line.a = pointSet[1];
line.b = pointSet[2];
line2.a = pointSet[3];
line2.b = pointSet[4];
if((line.a.x-line.b.x)*(line2.a.y-line2.b.y)!=(line2.a.x-line2.b.x)*(line.a.y-line.b.y))
return 2;
return 1;
case5
首先求焦点,然后判断是否在两条直线里面就行了,后面我把它封装到了Line类里面了。
Line line2= new Line();
line.a = pointSet[1];
line.b = pointSet[2];
line2.a = pointSet[3];
line2.b = pointSet[4];
if(line2.slope()==line.slope()){
System.out.print("is parallel lines,have no intersection point");
return 4;
}
Point point= line.intersection(line2);
System.out.printf(point.x+","+point.y+" ");
if((point.x<Math.max(line.a.x,line.b.x)&&point.x>Math.min(line.a.x,line.b.x))||(point.x<Math.max(line2.a.x,line2.b.x)&&point.x>Math.min(line2.a.x,line2.b.x)))
System.out.printf("true");
else
System.out.printf("false");
}
return 5;
slope()
简单的(y1-y2)/(x1-x2),判断一下斜率是否为0就行。
double slope(){//斜率
if(this.a.x==this.b.x)
return 0;
return (this.a.y-this.b.y)/(this.a.x-this.b.x);
}
intercept()
也是一个公式的解决方法,用来为求两条直线是否是同一条直线做铺垫的。
double intercept() {//截距
return this.a.x-(this.slope())*this.a.y;
}
pointVerticalDistanc()
高中点到直线距离公式,死去的高中数学突然攻击我hhhh。
double pointVerticalDistanc(Point c){//点到线距离
if(this.a.x==this.b.x)
return Math.abs(c.x-this.a.x);
if(this.a.y==this.b.y)
return Math.abs(c.y-this.a.y);
return Math.abs((this.a.y-this.b.y)*c.x+(this.b.x-this.a.x)*c.y+this.a.x*this.b.y-this.a.y*this.b.x)/
Math.sqrt((this.a.y-this.b.y)*(this.a.y-this.b.y)+(this.a.x-this.b.x)*(this.a.x-this.b.x));
}
7-3 点线形系列3-三角形的计算
本次博客的最难题来了。简单分析一下这题的五个case,除了第四个很难之外,其他case其实都还好,各种格式错误、输入错误来来回回折磨我几个小时,我的强迫症一发作就必须把前面的case过掉才会安心做其他的case,然后就是疯狂提交:
这也是一个调试小技巧,看懂掌声。
按照规矩,咱们继续来看看题:
1:输入三个点坐标,判断是否是等腰三角形、等边三角形,判断结果输出true/false,两个结果之间以一个英文空格符分隔。
2:输入三个点坐标,输出周长、面积、重心坐标,三个参数之间以一个英文空格分隔,坐标之间以英文","分隔。
3:输入三个点坐标,输出是钝角、直角还是锐角三角形,依次输出三个判断结果(true/false),以一个英文空格分隔,
4:输入五个点坐标,输出前两个点所在的直线与三个点所构成的三角形相交的交点数量,如果交点有两个,则按面积大小依次输出三角形被直线分割成两部分的面积。若直线与三角形一条线重合,输出"The point is on the edge of the triangle"
5:输入四个点坐标,输出第一个是否在后三个点所构成的三角形的内部(输出in the triangle/outof triangle)。
必须使用射线法,原理:由第一个点往任一方向做一射线,射线与三角形的边的交点(不含点本身)数量如果为1,则在三角形内部。如果交点有两个或0个,则在三角形之外。若点在三角形的某条边上,输出"on the triangle"
简单解读一下:1、判断三角形两条或者三条边是不是相等;2、输出周长面积重心;3、判断三角形内是否有钝角和直角;4、判断三角形和直线焦点,如果被分割输出被分割后面积;5、判断点是否在三角形内。浅谈一下,难度最高的肯定是case4,折磨了我巨久hhhh。
摆烂下次一定。
然后我们按类来讲讲我的代码。
case1
点线距离公式直接用,就前面7-1封装的方法。
int num = 0;
double[] distance = new double [5];
distance[1]=pointSet[1].DistanceCalculation(pointSet[2]);
distance[2]=pointSet[1].DistanceCalculation(pointSet[3]);
distance[3]=pointSet[2].DistanceCalculation(pointSet[3]);
Arrays.sort(distance,0,4);
// System.out.printf(distance[1]+" "+distance[2]+" "+distance[3]+"\n");
if(distance[1]+distance[2]<=distance[3])
return -3;
if(distance[1]==distance[2]||distance[2]==distance[3]||distance[3]==distance[1])
System.out.printf("true ");
else
System.out.printf("false ");
if(distance[1]==distance[2]&&distance[1]==distance[3]&&distance[3]==distance[2])
System.out.printf("true");
else
System.out.printf("false");
case2
周长就是三点距离和,面积是点到直线距离乘上直线长度,重心是三点横纵坐标之和的三分之一。
else if (x == 2) {
double[] distance = new double [5];
distance[1]=pointSet[1].DistanceCalculation(pointSet[2]);
distance[2]=pointSet[1].DistanceCalculation(pointSet[3]);
distance[3]=pointSet[2].DistanceCalculation(pointSet[3]);
Arrays.sort(distance,0,4);
if(distance[1]+distance[2]<=distance[3])
return -3;
System.out.printf(printDouble(distance[1]+distance[2]+distance[3])+" "+printDouble(Math.sqrt((distance[1]+distance[2]+distance[3])*(distance[1]+distance[2]-distance[3])*(distance[1]+distance[3]-distance[2])*(distance[2]+distance[3]-distance[1]))/4)+" "+printDouble((pointSet[1].x+pointSet[2].x+pointSet[3].x)/3)+","+printDouble((pointSet[1].y+pointSet[2].y+pointSet[3].y)/3));
case3
向量法完美解决。
double[] distance = new double [5];
distance[1] = pointSet[1].DistanceCalculation(pointSet[2]);
distance[2] = pointSet[1].DistanceCalculation(pointSet[3]);
distance[3] = pointSet[2].DistanceCalculation(pointSet[3]);
Arrays.sort(distance,0,4);
if(distance[1]+distance[2]<=distance[3])
return -3;
if((int)(distance[1]*distance[1])+(int)(distance[2]*distance[2])==(int)(distance[3]*distance[3]))
System.out.printf("false true false");
else if(distance[1]*distance[1]+distance[2]*distance[2]>distance[3]*distance[3])
System.out.printf("false false true");
else
System.out.printf("true false false");
case4
判断几个连接点直接用上个题目case5的代码就行,面积计算如下图:
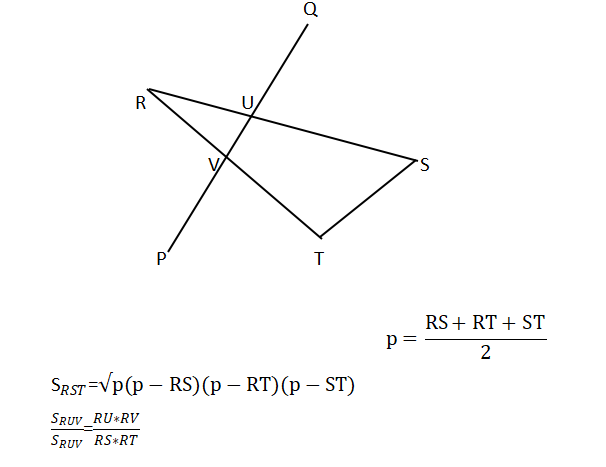
if(pointSet[1].x==pointSet[2].x&&pointSet[1].y==pointSet[2].y) {
System.out.printf("points coincide");
return 5;
}
double[] distance = new double [5];
if((pointSet[5].x==pointSet[3].x&&pointSet[3].x==pointSet[4].x)||(pointSet[5].y==pointSet[3].y&&pointSet[3].y==pointSet[4].y))
return -3;
line.a=pointSet[1];line.b = pointSet[2];
Triangle tri = new Triangle();
tri.a = new Line();
tri.b = new Line();
tri.c = new Line();
tri.a.a = pointSet[3];tri.a.b = pointSet[4];
tri.b.a = pointSet[3];tri.b.b = pointSet[5];
tri.c.a = pointSet[4];tri.c.b = pointSet[5];
int num = 0;
if(line.judgeIntersection(tri.a)==1)
num++;
if(line.judgeIntersection(tri.b)==1)
num++;
if(line.judgeIntersection(tri.c)==1)
num++;
if(num==0) {
System.out.printf("0");
return 5;
}
if(num==1||(num==2&&(line.sameIntersection(tri.c, tri.a)||line.sameIntersection(tri.b, tri.a)||line.sameIntersection(tri.c, tri.b)))){
System.out.printf("1");
return 5;
}
System.out.printf("2 ");
double s = tri.area(),s2=0;
if(line.judgeIntersection(tri.c)==-1|| line.sameIntersection(tri.c, tri.a)|| line.sameIntersection(tri.b, tri.c)){
s2 = areaCalculation(pointSet[3],pointSet[4],pointSet[5],line,s);
}
else if(line.judgeIntersection(tri.b)==-1||line.sameIntersection(tri.a, tri.b)){
s2= areaCalculation(pointSet[4],pointSet[3],pointSet[5],line,s);
}
else
s2 = areaCalculation(pointSet[5],pointSet[4],pointSet[3],line,s);
System.out.printf(printDouble(Math.min(s2,s-s2))+" "+printDouble(Math.max(s2,s-s2)));
case5
case5用点射法固定好了,代码如下。
double[] distance = new double [5];
if((pointSet[2].x==pointSet[3].x&&pointSet[3].x==pointSet[4].x)||(pointSet[2].y==pointSet[3].y&&pointSet[3].y==pointSet[4].y))
return -3;
Triangle a= new Triangle(),b= new Triangle(),c= new Triangle(),d= new Triangle();
a.b= new Line();a.a= new Line();a.c = new Line();
b.b= new Line();b.a= new Line();b.c = new Line();
c.b= new Line();c.a= new Line();c.c = new Line();
d.b= new Line();d.a= new Line();d.c = new Line();
a.a.a=pointSet[2];a.a.b = pointSet[3];
a.b.a=pointSet[2];a.b.b = pointSet[4];
a.c.a=pointSet[4];a.c.b = pointSet[3];
b.a.a=pointSet[1];b.a.b = pointSet[3];
b.b.a=pointSet[1];b.b.b = pointSet[4];
b.c.a=pointSet[4];b.c.b = pointSet[3];
c.a.a=pointSet[2];c.a.b = pointSet[1];
c.b.a=pointSet[2];c.b.b = pointSet[4];
c.c.a=pointSet[4];c.c.b = pointSet[1];
d.a.a=pointSet[2];d.a.b = pointSet[3];
d.b.a=pointSet[2];d.b.b = pointSet[1];
d.c.a=pointSet[1];d.c.b = pointSet[3];
if(d.area()==0||b.area()==0||c.area()==0)
System.out.println("on the triangle");
else if(Math.abs(a.area()-b.area()-c.area()-d.area())<0.0005)
System.out.printf("in the triangle");
else
System.out.println("outof the triangle");
sameIntersection()
boolean sameIntersection(Line line1,Line line2){//判断相交点是否相同
Point point1=this.intersection(line1),point2=this.intersection(line2);
if(point2.x==point1.x&&point1.y==point2.y)
return true;
return false;
}
vectorComputation()
判断点是否在线内好方法
public static double vectorComputation(Point a,Point b,Point c){//计算点线是否相交
double x1 = a.x-c.x, y1=a.y-c.y,x2=b.x-c.x,y2=b.y-c.y;
return x1*y2-x2*y1;
}
Triangle
除了之前用的一些类外,针对第三题我重新设置了一个类Triangle,主要功能是计算三角形的面积。
public class Triangle {
Line a;
Line b;
Line c;
public Triangle() {
}
double area() {
double p = (Math.sqrt((this.a.a.x - this.a.b.x) * (this.a.a.x - this.a.b.x) + (this.a.a.y - this.a.b.y) * (this.a.a.y - this.a.b.y)) + Math.sqrt((this.b.a.x - this.b.b.x) * (this.b.a.x - this.b.b.x) + (this.b.a.y - this.b.b.y) * (this.b.a.y - this.b.b.y)) + Math.sqrt((this.c.a.x - this.c.b.x) * (this.c.a.x - this.c.b.x) + (this.c.a.y - this.c.b.y) * (this.c.a.y - this.c.b.y))) / 2.0;
return Math.sqrt(p * (p - Math.sqrt((this.a.a.x - this.a.b.x) * (this.a.a.x - this.a.b.x) + (this.a.a.y - this.a.b.y) * (this.a.a.y - this.a.b.y))) * (p - Math.sqrt((this.b.a.x - this.b.b.x) * (this.b.a.x - this.b.b.x) + (this.b.a.y - this.b.b.y) * (this.b.a.y - this.b.b.y))) * (p - Math.sqrt((this.c.a.x - this.c.b.x) * (this.c.a.x - this.c.b.x) + (this.c.a.y - this.c.b.y) * (this.c.a.y - this.c.b.y))));
}
}
踩坑心得
这三次作业有很多巨让人难受的坑,有时候写着写着就摆烂了,一个点过不去就像蚂蚁在身上爬。第一个碰到的坑当然是第一次作业的第二题,要转换成float类型,要不然精度一直错hhhh,在不断的试错后,才成功。然后就是7-9,他有个转义符点的判断,这个也是蒙了一下。第二次作业最麻烦的就是最后一题,一直有三个case过不去,主要原因就是没有用正则表达式,所以正则表达式还是很重要的,要不然就得多用巨多if和else。
回头看过去,没想到第三次作业的第二题wa的次数要比第三题多,其实也就是距离的精度问题以及正则表达式错误hhhh,第三题是我wa麻了的一题,题干中第四个case的格式判断我放在了外面,然后就会有各种莫名其妙的答案错误,而后改到case4里面后,仍然wa,而后发现是判断的问题。第四个case是我最头疼的,一开始我借用了别人的数学方法,结果一直错,直到我拿出纸笔计算才发现,那个公式根本就是错误的

这起码浪费了我三个小时的时间,期间我一直在根据那个公式推理hhhh。后面我还少了一个零焦点的判断,以至于我一直以为是精度的问题,最主要的是直线过端点的情况没有考虑完全,导致后来的公式也是一直错误hhhhh,精度方面倒没啥问题。
改进建议
不应该偷懒不学正则表达式,其实在第二次作业的时候我就以及看过正则表达式了,我还把别人使用正则表达式的代码贴了出来,有兴趣的可以点那几个发绿的字去看看。另外就是圈复杂度太高,下次写的时候一定要加强封装,让圈复杂度降低到10。
总结
此三次练习,让我学会了基本的数据输入输出,简单的数据处理,还有字符串的各项操作,题目集难度由浅入深,我逐步学习了正则表达式、基本语法、封装等专业知识,由此我也看到了自己学习的东西尚浅,对于许多知识点掌握得仍旧不熟练,我应当在后期的学习中巩固基础,同时拓宽知识面,如自学正则表达式等有助于让代码更加简洁的方法。也让我学会了很多关于Java的字符串处理的语法和方法,同时我对于类的使用还不是很熟练,要加强面向对象理念。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号