结对编程作业
我们的小队——青春喂了软工队
话不多说赶紧放上我们作业的github链接
GitHub:GITHUB
分工
在查找完相关资料后,我们将主要任务拆分成为了两小趴~
| 分工 | 曾丽莉 | 郭畅 |
|---|---|---|
| 原型设计(微信小程序) | AI算法 | |
| 我们的照片哈哈哈 |

两个憨憨在讨论原型设计
原型设计
原型设计
坦白来说,“原型设计”是我第一次接触的词语,在查了大量资料过后,才发现原型设计在一个软件的诞生之前有着重要的角色,
一个好的原型设计足以确定整个软件的方向,相当于一个流程图,此次的作业中,我使用了Mockplus来做此次的原型设计(就新手必备!太好操作了也)
先放上一张总的各个界面的图(在两个人讨论过后,这次的图片华容道我们想做成一个微信小程序,原型设计是基于手机屏幕实现的)
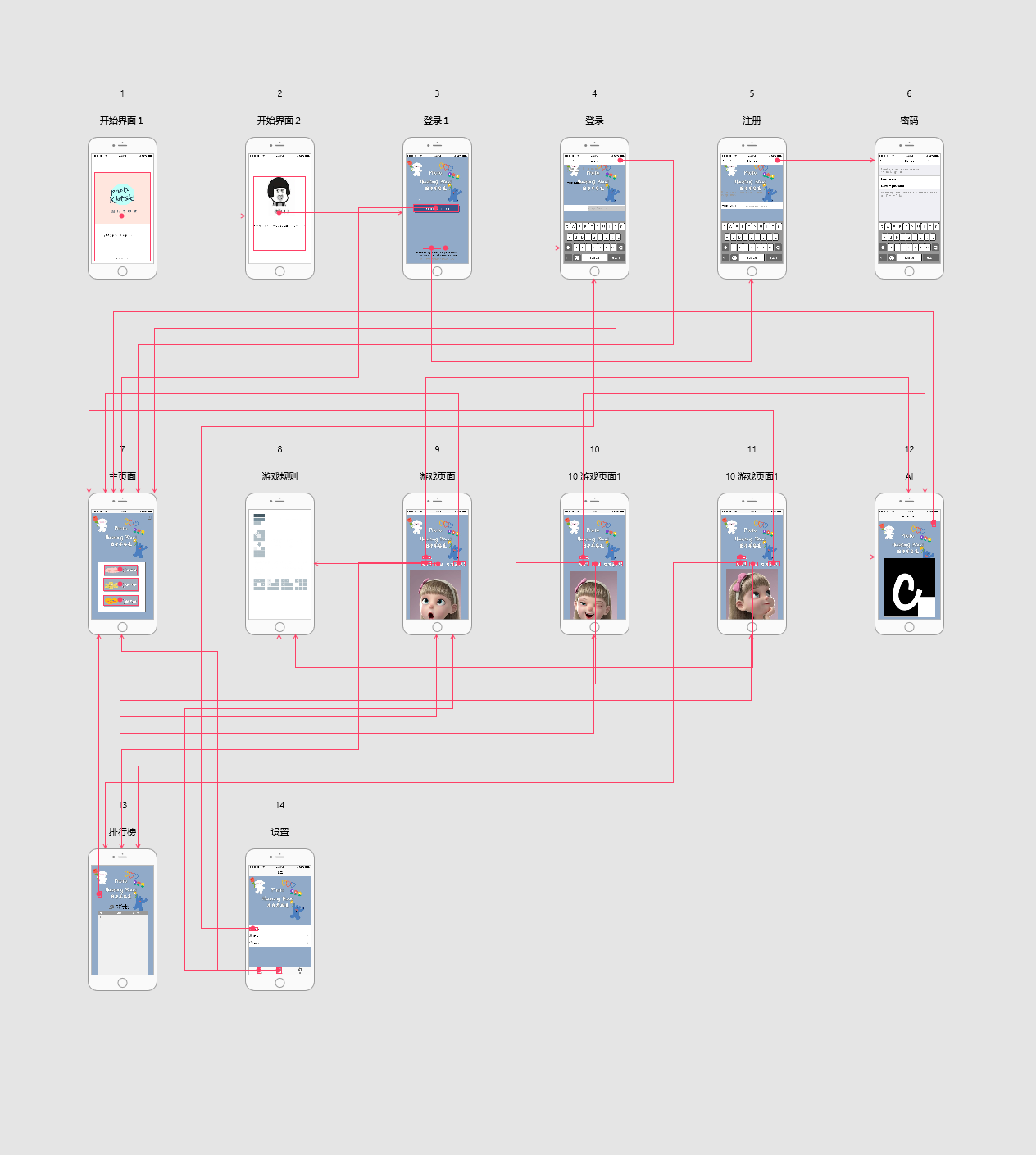
1.游戏的主页面
一个游戏最基础的是什么!头脑里面马上想起来的就是游戏的界面,我们总共分成三个难度等级,分别是33和44和5*5
直接在主面板上面点击即可转到相应的界面,每个界面先划分了5个小模块,分别是返回主页,游戏规则,原图提示,排行榜,以及不能过关的时候的AI演示.
(由于技术原因,在原型设计的时候,我们先用一张照片来表示随机生成的棋盘形状)




2.导入和登陆注册页面
在设计完成基本游戏界面后,接下来扩展的是登陆注册的功能,原型图如下:
由于登陆涉及网站服务器的绑定,实在不会操作,在后来的实现中没有完成该功能。。。


3.各个模块小功能
有了整个大致的框架,接下来要做的就是细化每个小模块的功能,计划总共有三个小模块,分别是游戏规则说明,排行榜,AI演示


4.遇到的困难以及解决方案
一开始使用的原型设计是AXURE,有“亿”点点过于专业了,在尝试之后,只会拉一个框,剩下的只会乱按,在不断的百度之后,发现了Mockplus这个神仙软件!非常好上手,无论是建立页面之间的连接,或者是在搭建整个页面的时候,小组件很清晰的让你知道怎么使用,不足的是,在实现插入能够活动的方块这个操作,实现起来有点复杂,到了最后也没有将其实现(十分遗憾)
最后微信小程序实现主页面的设计见GitHub

AI算法
代码实现
1)网络接口
- 因为之前从来没有接触过json还有base64编码,刚开始还是一脸懵的
- 对base64解码,直接使用python的base64里的函数进行解析就好啦。
import base64
with open("D:\\pycharm\\三阶数字华容道最优解(更新版)\\三阶数字华容道最优解(更新版)\\q_table\\test.txt","r") as f:
imgdata = base64.b64decode(f.read())
file = open('D:\\pycharm\\三阶数字华容道最优解(更新版)\\三阶数字华容道最优解(更新版)\\img2\\img\\test.jpg','wb')
file.write(imgdata)
file.close()
这个解码还是比较简单的,直接把图片保存下来
2)代码组织与内部设计实现
MyFrame.py

Generator.py
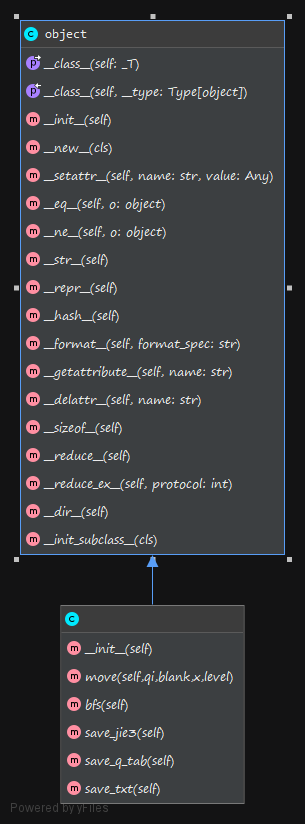
Qipan.py
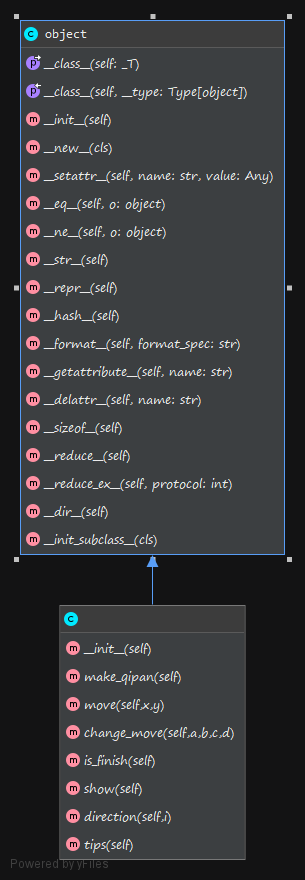
Prediction.py
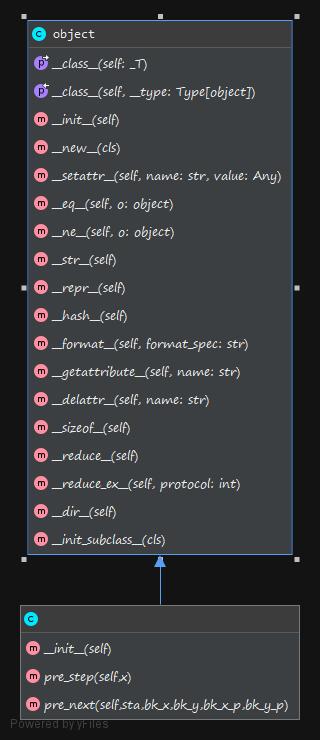
3)算法的关键与关键实现部分流程图
1.前期对解码出来的图片进行分割,并求出对应图片及乱序矩阵
分割:直接可对所有图片,将其转化为正方形,不够的地方使用白色填充,进行切割
求解图片:将图片转化为像素矩阵,进行一一对比
2.解题代码:使用BFS进行对数据进行预处理后,求解
定义:
- 状态(S):每个棋盘的布局称为一个状态,其中状态 [[1,2,3],[4,5,6],[7,8,9]] 称为零状态
- 代价(C):从当前状态到零状态所需的最小步数
- 预处理:从零状态开始,使用BFS遍历每个状态,在遍历的同时,给每个状态标记遍历的层号(零状态为第0层),即代价。
为防止重复遍历某些状态,使用一个字典保存遍历过的状态及其对应层号,即 q_tab={s1:c1, s2:c2, ..., s181440:c181440}。 - 归位:在q_tab 中查找与当前状态相连的状态的代价,选择代价最小的状态作为下一步决策。
解题——流程图:
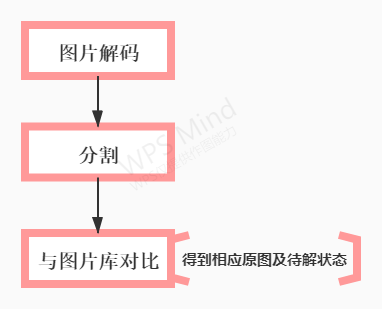
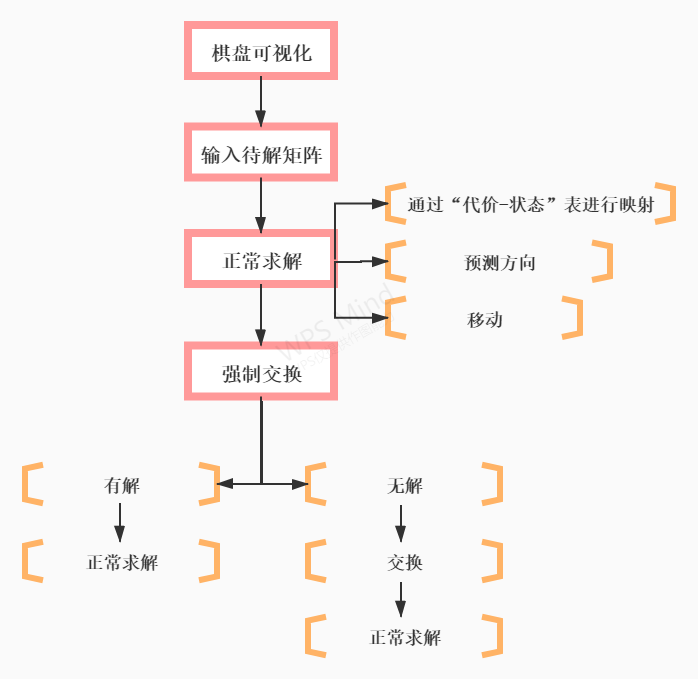
4)重要代码片段
数据预处理:
- 通过 BFS 构建 q_tab 表,即“状态->代价”映射表
import numpy as np
class Generator:
def __init__(self):
self.n=3 #棋盘阶数
self.N=self.n*self.n #棋盘中棋子个数(包含空格)
self.dict={} #用于判重
self.que_qi=[] #用于广度优先搜索中,辅助队列(存储棋盘)
self.que_bk=[] #用于广度优先搜索中,辅助队列(存储空格)
self.que_lv=[] #用于广度优先搜索中,辅助队列(存储层数)
self.deep=31 #遍历深度
self.X=[-1,-self.n,1,self.n] #棋子移动方位
self.qi_init="123456789" #初始棋盘布局
def move(self,qi,blank,x,level): #将空格 blank 移向 x 位置
if x<0 or x>=self.N or blank==x:
return
if abs(blank%self.n-x%self.n)>1:
return
if blank<x:
temp=qi[:blank]+qi[x]+qi[blank+1:x]+qi[blank]+qi[x+1:]
else:
temp=qi[:x]+qi[blank]+qi[x+1:blank]+qi[x]+qi[blank+1:]
if temp in self.dict:
return
self.dict[temp]=level+1
self.que_qi=[temp]+self.que_qi
self.que_bk=[x]+self.que_bk
self.que_lv=[level+1]+self.que_lv
def bfs(self): #广度优先搜索
self.que_qi=[self.qi_init]+self.que_qi
self.que_bk=[9-1]+self.que_bk # 根据题目中空格所在位置对应的值进行修改
self.que_lv=[0]+self.que_lv
self.dict[self.qi_init]=0
lv=0
while lv<self.deep and self.que_qi!=[]:
qi=self.que_qi.pop()
bk=self.que_bk.pop()
lv=self.que_lv.pop()
direction=np.random.permutation(4) #生成0~3的随机排列
for i in direction:
x=bk+self.X[i]
self.move(qi,bk,x,lv)
def save_jie3(self): #保存样本数据
num=len(self.dict)
data=np.zeros((num,self.N))
label=np.zeros(num)
i=0
for k in self.dict:
label[i]=self.dict[k]
for j in range(self.N):
data[i][j]=float(k[j])
i+=1
np.savez("jie3.npz",data=data,label=label)
def save_q_tab(self): #保存Query表
k=list(self.dict.keys())
v=list(self.dict.values())
np.savez("q_tab.npz",k=k,v=v)
def save_txt(self): #保存为TXT文档
file=open("jie3.txt",'w')
s=""
for k in self.dict:
v=self.dict[k]
for i in range(self.N):
s+=k[i]+' '
s+=str(v)+'\n'
file.write(s)
file.flush()
file.close()
gen=Generator()
gen.bfs()
gen.save_jie3()
gen.save_q_tab()
gen.save_txt()
运行完以后,q_tab.npz 保存了“状态 -> 代价”的映射,jie3.txt 的部分内容如下:

可得到代价分布图
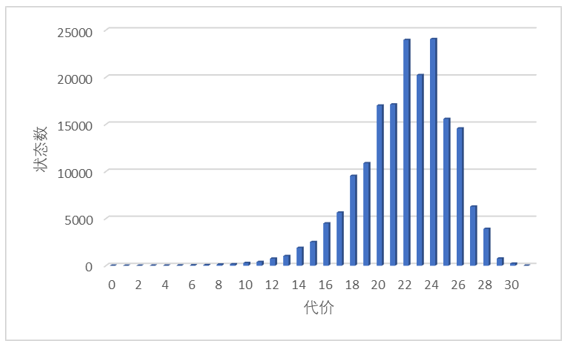
归位:
最重要的是预测下一步走向:
调用代价函数得到的“状态--代价”表,根据随机序列,寻找代价最小的序列为下一步对应的状态矩阵
class Prediction:
def __init__(self):
self.n=3
self.N=self.n*self.n
q_tab=np.load('q_tab.npz')
k=q_tab['k']
v=q_tab['v']
self.q_tab=dict(zip(k,v)) #构建Q表
self.X=[-1,0,1,0] #方向
self.Y=[0,-1,0,1]
def pre_step(self,x): #预测状态 x 对应的步数
x=np.array(x).reshape(1,-1)
k = ""
for i in range(self.N):
k+=str(x[0,i])
v=self.q_tab.get(k,-1)
return v
def pre_next(self,sta,bk_x,bk_y,bk_x_p,bk_y_p): #预测下一步往哪个方向走
step=[10000,10000,10000,10000]
direction=np.random.permutation(4) #生成0~3的随机排列
for i in direction:
x=bk_x+self.X[i]
y=bk_y+self.Y[i]
if x<0 or x>=self.n or y<0 or y>=self.n or x==bk_x_p and y==bk_y_p:
continue
t=sta[x][y]
sta[x][y]=7 # 修改空格位置的值
sta[bk_x][bk_y]=t
step[i]=self.pre_step(sta)
sta[x][y]=t
sta[bk_x][bk_y]=7 # 根据移动格修改
return np.argmin(step)
最后定义棋盘,采用多线程实现:主线程负责监听用户动作(点击“开始/暂停”按钮),子线程负责棋盘更新。
主线程:
子线程:
class Qipan:
def __init__(self):
self.n=3
self.N=self.n*self.n
self.init=np.arange(1,self.N+1).reshape(self.n,self.n)
self.qipan = self.init.copy()
self.bk_x=1
self.bk_y=0 # 打乱后的空格位置
self.bk_x_p=-1
self.bk_y_p=-1
self.pre=Prediction()
self.started=False #标记是否开始
self.X=[-1,0,1,0]
self.Y=[0,-1,0,1]
self.dir = []
def make_qipan(self): #生成棋盘
print("请输入待解数组")
string = sys.stdin.readline().strip()
arr = []
count = 0
for i in string:
try:
arr.append(int(i))
except:
if i == '[':
count += 1
pass
cols = int(len(arr) / count)
grid = []
cur = []
for i in arr:
if len(cur) <= cols:
cur.append(i)
else:
grid.append(cur)
cur = []
cur.append(i)
grid.append(cur)
self.qipan=grid
self.step=0 #提示计步
self.started=True #标记是否开始
def move(self,x,y): #移动棋子
if x<0 or x>=self.n or y<0 or y>=self.n:
return
self.qipan[self.bk_x][self.bk_y]=self.qipan[x][y] # 交换值
self.qipan[x][y]=1 # 空格位置的值
self.bk_x_p=self.bk_x #交换位置
self.bk_y_p=self.bk_y
self.bk_x=x
self.bk_y=y
def change_move(self,a,b,c,d): # 交换棋子
t = self.qipan[a][b]
self.qipan[a][b] = self.qipan[c][d]
self.qipan[c][d] = t
def is_finish(self): #判断游戏是否结束
for i in range(self.n):
for j in range(self.n):
if self.qipan[i][j]!=self.init[i][j]:
return False
print("".join(self.dir))
return True
def show(self): #打印当前棋盘状态
s=""
for i in range(self.n):
for j in range(self.n):
if self.qipan[i][j]==1: # 当位置是空格处的值时,打印空格
s+=" "
else:
s+=str(self.qipan[i][j])+" "
s+="\n"
print(s)
def direction(self,i):
if i == 0:
print("w")
dire = 'w'
if i == 1:
print("a")
dire = 'a'
if i == 2:
print("s")
dire = 's'
if i == 3:
print("d")
dire = 'd'
self.dir.append(dire)
def tips(self):
if self.step != 13-1: # 不在强制交换的步数中
i = self.pre.pre_next(self.qipan, self.bk_x, self.bk_y, self.bk_x_p, self.bk_y_p)
x = self.bk_x + self.X[i]
y = self.bk_y + self.Y[i]
self.move(x, y)
self.direction(i)
self.step += 1
print("step", self.step)
print("进行交换的棋子:", "(", x, ",", y, ")")
self.show()
else: # 在强制交换的步数中
self.show()
print("请输入要交换的值的坐标:两个")
print("第一个")
a, b = map(eval, input('两个值:').split())
print("第二个")
c, d = map(eval, input('两个值:').split())
self.change_move(a,b,c,d) # 移动强制交换的两个值
s = self.pre.pre_step(self.qipan) # 移动后确定是否有解
if s == -1: #强制交换后无解
print("无解,需要进行手动交换")
# 打印棋盘
self.show()
print("请选择需要交换的数值")
# 输入两个值
p = -1 # 因为无解返回-1
while(p == -1): # 当为-1即为无解时,进入循环
print("请输入要交换的值的坐标:两个")
print("第一个")
g, h = map(eval, input('两个值:').split())
print("第二个")
z, c = map(eval, input('两个值:').split())
self.change_move(g,h,z,c)
p = self.pre.pre_step(self.qipan) # 如果有解那p将不为-1,退出循环
self.change_move(z,c,g,h)
# 退出循环说明有解了
print("开始正常运行")
self.change_move(g,h,z,c)
i = self.pre.pre_next(self.qipan, self.bk_x, self.bk_y, self.bk_x_p, self.bk_y_p)
x = self.bk_x + self.X[i]
y = self.bk_y + self.Y[i]
self.move(x, y)
self.direction(i)
self.step += 1
print("step", self.step)
print("进行交换的棋子:", "(", x, ",", y, ")")
self.show()
else: #强制交换后有解
i = self.pre.pre_next(self.qipan, self.bk_x, self.bk_y, self.bk_x_p, self.bk_y_p)
x = self.bk_x + self.X[i]
y = self.bk_y + self.Y[i]
self.move(x, y)
self.direction(i)
self.step += 1
print("step", self.step)
print("进行交换的棋子:", "(", x, ",", y, ")")
self.show()
5)性能分析与改进
性能分析:(使用pycharm里的分析)没错又是它,嘻嘻嘻
主函数的性能分析:
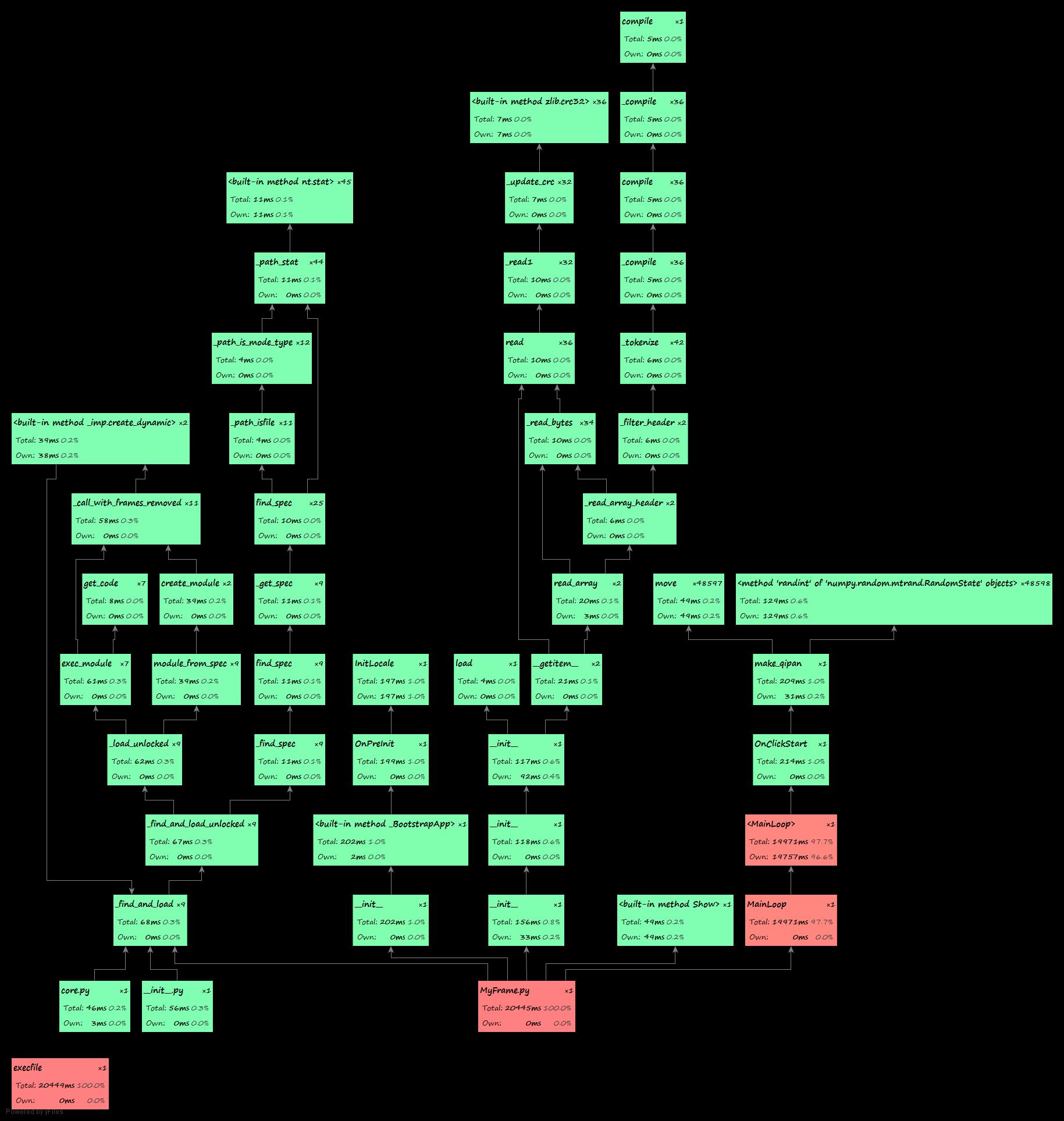
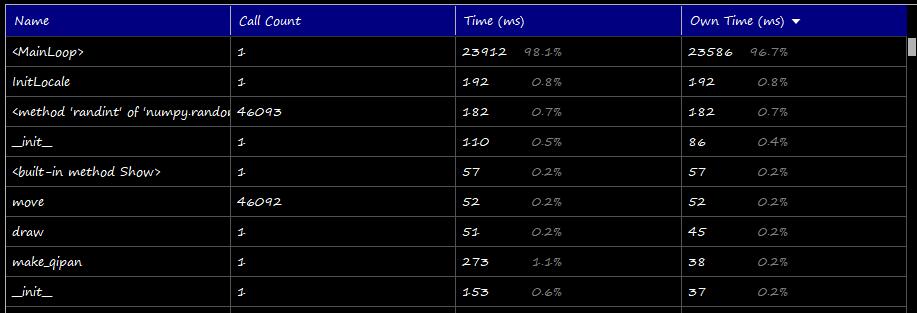
生成“状态—代价映射”表的性能分析:
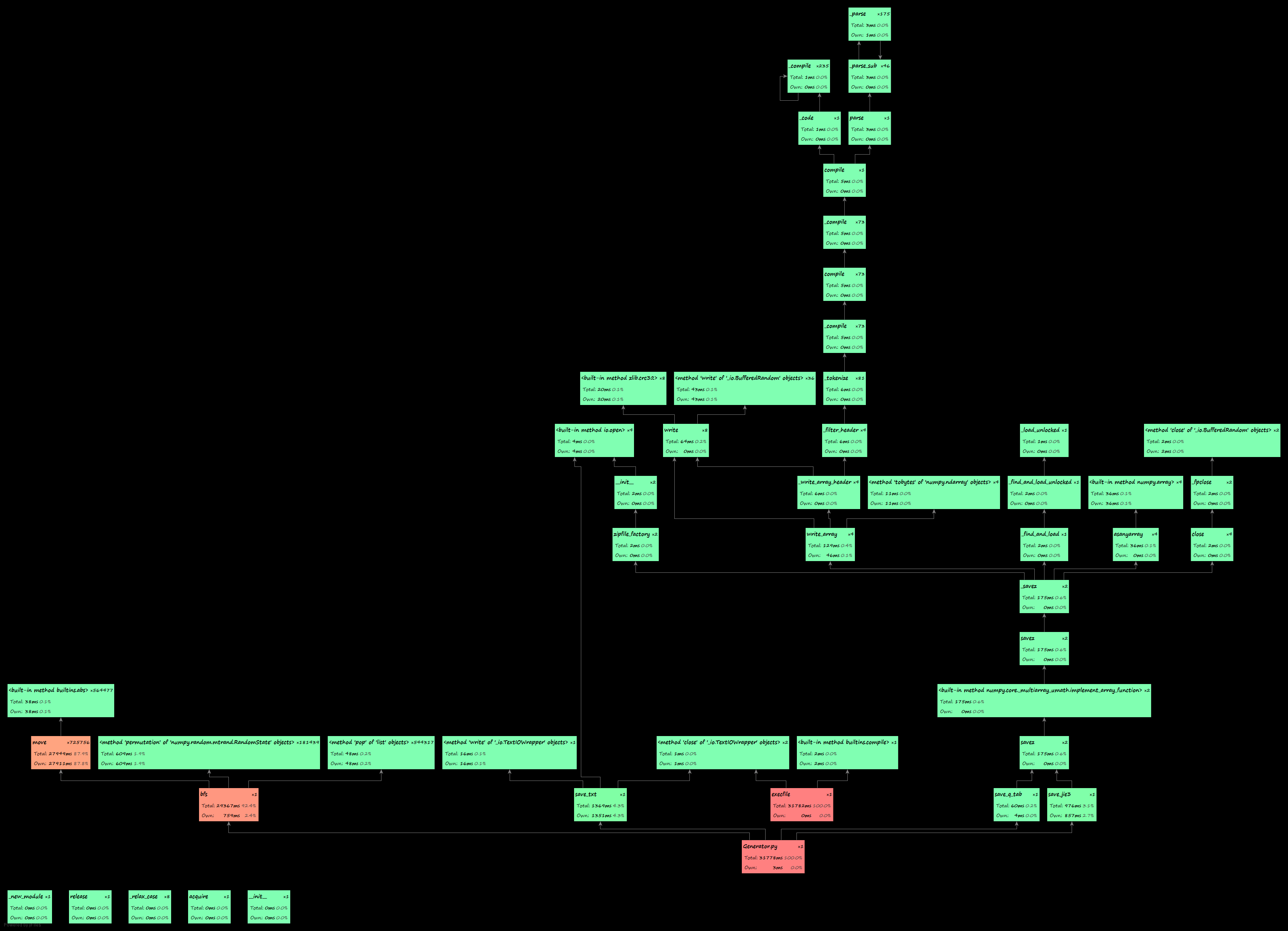
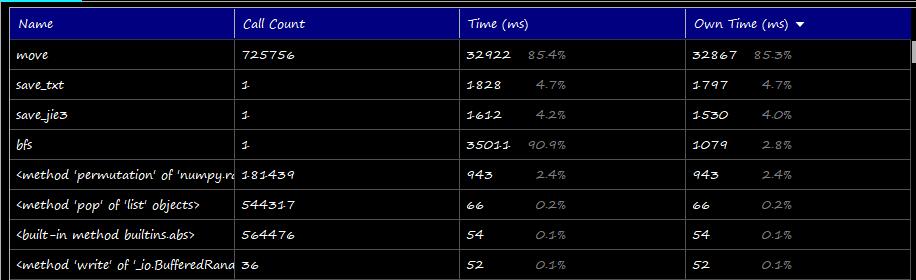
改进:
由于刚开始的算法只是随机生成棋盘进行求解,所以要做的改进就是自定义棋盘进行求解
自定义输入棋盘,并将自定义棋盘赋值给self.qipan使得可以对棋盘进行调用
def make_qipan(self): #生成棋盘
print("请输入待解数组")
string = sys.stdin.readline().strip()
arr = []
count = 0
for i in string:
try:
arr.append(int(i))
except:
if i == '[':
count += 1
pass
cols = int(len(arr) / count)
grid = []
cur = []
for i in arr:
if len(cur) <= cols:
cur.append(i)
else:
grid.append(cur)
cur = []
cur.append(i)
grid.append(cur)
self.qipan=grid
self.step=0 #提示计步
self.started=True #标记是否开始
强制转换,增加新函数change_move,以及强制交换无解做法,满足强制交换要求
def change_move(self,a,b,c,d): # 交换棋子
t = self.qipan[a][b]
self.qipan[a][b] = self.qipan[c][d]
self.qipan[c][d] = t
def tips(self):
if self.step != 13-1: # 不在强制交换的步数中....................................................................
i = self.pre.pre_next(self.qipan, self.bk_x, self.bk_y, self.bk_x_p, self.bk_y_p)
x = self.bk_x + self.X[i]
y = self.bk_y + self.Y[i]
self.move(x, y)
self.direction(i)
self.step += 1
print("step", self.step)
print("进行交换的棋子:", "(", x, ",", y, ")")
self.show()
else: # 在强制交换的步数中
self.show()
print("请输入要交换的值的坐标:两个")
print("第一个")
a, b = map(eval, input('两个值:').split())
print("第二个")
c, d = map(eval, input('两个值:').split())
self.change_move(a,b,c,d) # 移动强制交换的两个值
s = self.pre.pre_step(self.qipan) # 移动后确定是否有解
if s == -1: #强制交换后无解
print("无解,需要进行手动交换")
# 打印棋盘
self.show()
print("请选择需要交换的数值")
# 输入两个值
p = -1 # 因为无解返回-1
while(p == -1): # 当为-1即为无解时,进入循环
print("请输入要交换的值的坐标:两个")
print("第一个")
g, h = map(eval, input('两个值:').split())
print("第二个")
z, c = map(eval, input('两个值:').split())
self.change_move(g,h,z,c)
p = self.pre.pre_step(self.qipan) # 如果有解那p将不为-1,退出循环
self.change_move(z,c,g,h)
# 退出循环说明有解了
print("开始正常运行")
self.change_move(g,h,z,c)
i = self.pre.pre_next(self.qipan, self.bk_x, self.bk_y, self.bk_x_p, self.bk_y_p)
x = self.bk_x + self.X[i]
y = self.bk_y + self.Y[i]
self.move(x, y)
self.direction(i)
self.step += 1
print("step", self.step)
print("进行交换的棋子:", "(", x, ",", y, ")")
self.show()
else: #强制交换后有解
i = self.pre.pre_next(self.qipan, self.bk_x, self.bk_y, self.bk_x_p, self.bk_y_p)
x = self.bk_x + self.X[i]
y = self.bk_y + self.Y[i]
self.move(x, y)
self.direction(i)
self.step += 1
print("step", self.step)
print("进行交换的棋子:", "(", x, ",", y, ")")
self.show()
还有一个失败的算法5555
使用神经网络映射 q_tab 表。基于神经网络的方法和使用 q_tab 表差不多,主要差别是:在预处理阶段,加了神经网络训练;在归位时,不在q_tab 表中查找代价,而是在神经网络中映射代价。神经网络的网络参数空间小于q_tab 表的空间,这样节省了不少内存空间。(不过是借鉴的,看不懂,没法继续了)
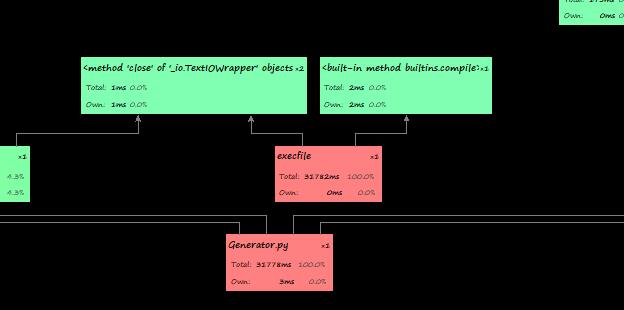
6)性能分析图和程序中消耗最大的函数
消耗最大的以及耗时最长的应该是Generator.py了,毕竟是肉眼可见的慢hhhhh
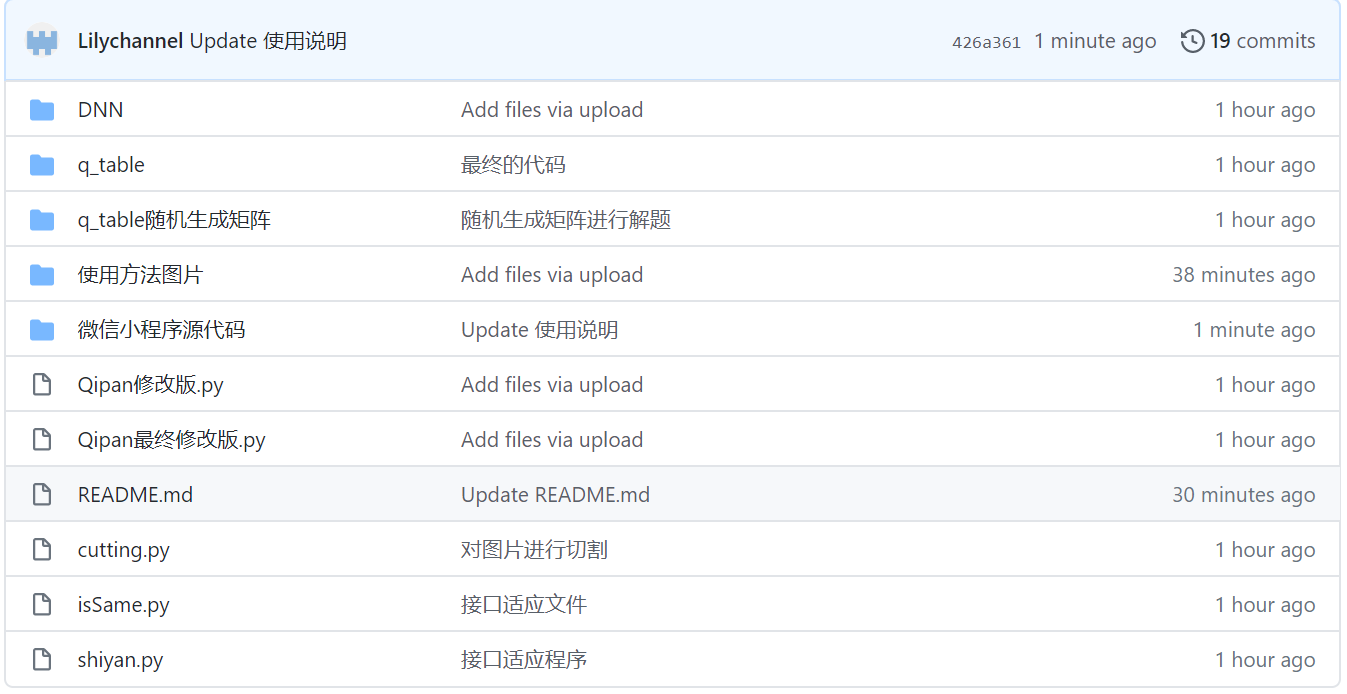
Github签入记录
遇到的异常
碰到最不好解决的异常,就是在修改代码,从随机生成棋盘到最后自定义棋盘的过程,每个类之间互相联系,修改代码要更加谨慎
由于使用了“代价——映射”表,所以程序其他程序只能等待该程序运行完,才能运行,由于表中生成的是所有可达排列,所以很浪费时间
在进行强制交换时,想要用“状态——代价”表判断有无解,怎样利用好这个表,是个问题
最后的解决
因为映射表中的内容,是可达状态到零状态的所有排列,所以,只要判断每一步生成的序列是否在表中,get()即可,不在则返回-1,
则当不为-1时,说明有解,为-1时,无解
无解时再进行一次自己交换,为了使交换会有解,每次交换都要进行判断是否为-1,再决定是否进行交换
但是最后又出现了一个问题,当需要交换的位置中有空格时,会发生混乱,还没有解决
只能运行两次代码,衔接起来求解,非常慢了可以说
有何收获
评价队友
值得学习的地方
UI设计第一次整喔,最后还整出小程序来啦,出乎意料surprise~
需要改进的地方
第一次搭档,经历了磨合,确实沟通方面有一些小阻碍,不过都解决啦yeah~
希望能更好
PSP和学习进度条
PSP
| PSP | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 25 |
| · Estimate | · 估计这个任务需要多少时间 | 30 | 25 |
| Development | 开发 | 1790 | 2084 |
| · Analysis | · 需求分析 (包括学习新技术) | 620 | 642 |
| · Design Spec | · 生成设计文档 | 60 | 55 |
| · Design Review | · 设计复审 | 30 | 32 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 30 |
| · Design | · 具体设计 | 300 | 310 |
| · Coding | · 具体编码 | 500 | 570 |
| · Code Review | · 代码复审 | 50 | 45 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 200 | 400 |
| Reporting | 报告 | 120 | 160 |
| · Test Report | · 测试报告 | 60 | 70 |
| · Size Measurement | · 计算工作量 | 30 | 50 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 40 |
| · 合计 | 1940 | 2269 |
学习进度条
| 第N周 | 新增代码(行) | 本周学习耗时(小时) | 累计学习耗时(小时) | 重要成长 |
|---|---|---|---|---|
| 1 | 256 | 20 | 20 | 初步掌握BFS以及代价映射思路 |
| 2 | 185 | 10 | 30 | 尝试使用DNN,理解思路(但未采用) |
| 3 | 56 | 6 | 36 | 用映射表的思路进行强制转换 |
| 4 | 185 | 6 | 42 | 图片像素化,矩阵相似 |


