（未完待续）学习机器学习必备的线性代数知识

 

（转载请注明出处：danscarlett的博客园）

参考资料出处：Biomimetic robotics and machine learning

一 矩阵

　　一个m×n的矩阵A是将按照m行、n列矩形形式的排列的一组标量值

　　矩阵A中第i行第j列的元素可以被写作A_ij或者a_ij。最准确的写法是 [A]_ij

1.矩阵加法

　　对于具有相同行数和列数的矩阵A和B，有

2.矩阵乘法

 　　对于一体个 l×n 矩阵A 和一个 n×m矩阵B, 它们的乘积 AB 是一个 l×m 的矩阵，其中的元素满足：

　　一般来说 BA ≠ AB。

　　如果BA = AB，那么我们称A和B可交换。

 

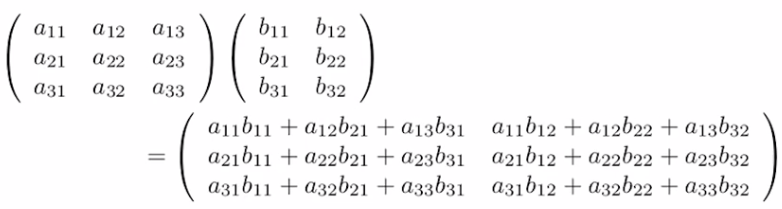
3. 单位矩阵

　　单位矩阵I的行数与列数相等，对角线上的元素都是1，除了对角线以外的其他地方都填充0.我们也可以用I_m来表示一个m×m的矩阵。

　　对于一个m×n的矩阵A，I_mA = AI_n = A。

　　用克罗内克符号表示单位矩阵的元素 [I]_ij ＝δ_ij

4.矩阵的转置

　　对于一个 n×m 的矩阵B，转置B^T 是一个m×n的矩阵，其中元素满足：

　　并且有

　　如果A,B,C三个矩阵可以作矩阵乘法，那么就存在：

　　

二 向量代数

 　　用 x 来表示一个 n维的列向量：

　

　　一个向量可以被视作是一个n×1的矩阵。

 

1 向量加法

 

2 标量乘法（内积）

 

　　向量的长度用 |x| 来表示。长度的平方是

　　对于一个单位向量x，有

x^Tx = 1

　　用自然几何解释向量内积：

　　θ是两向量之间的夹角。当两个向量的长度固定时，θ=0时，向量内积最大，此时一个向量是另一个的常数倍。如果内积 x^Ty = 0,那么x和y正交/垂直。