一、法向量定义
定义:如果 ,那么向量
,那么向量 叫做平面
叫做平面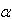 的法向量。平面
的法向量。平面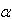 的法向量共有两大类(从方向上分),无数条。
的法向量共有两大类(从方向上分),无数条。
二、平面法向量的求法
1、内积法
在给定的空间直角坐标系中,设平面  的法向量
的法向量 =(x,y,1)[或
=(x,y,1)[或 =(x,1,z)或
=(x,1,z)或 =(1,y,z)],在平面
=(1,y,z)],在平面 内任找两个不共线的向量
内任找两个不共线的向量 ,
, 。由
。由
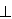
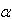 ,得
,得 ·
· =0且
=0且 ·
· =0,由此得到关于x,y的方程组,解此方程组即可得到
=0,由此得到关于x,y的方程组,解此方程组即可得到 。
。
2、
任何一个x,y,z的一次方程的图形是平面;反之,任何一个平面的方程是x,y,z的一次方程。Ax+By+Cz+D=0(A,B,C不同时为0),称为平面的一般方程。其法向量 =(A,B,C);若平面与3个坐标轴的交点为P(a,0,0),P(0,b,0),P(0,0,c),则平面方程为:
=(A,B,C);若平面与3个坐标轴的交点为P(a,0,0),P(0,b,0),P(0,0,c),则平面方程为: ,称此方程为平面的截距式方程,把它化为一般式即可求出它的法向量。
,称此方程为平面的截距式方程,把它化为一般式即可求出它的法向量。
3、外积法
设 ,
, 为空间中两个不平行的非零向量,其外积
为空间中两个不平行的非零向量,其外积 ×
× 为一长度等于|
为一长度等于| ||
|| |sinθ,(θ为
|sinθ,(θ为
 两者交角,且0<θ<π,而与
两者交角,且0<θ<π,而与 ,
, , 皆垂直的向量。通常我们采取“右手定则”,也就是右手四指由
, 皆垂直的向量。通常我们采取“右手定则”,也就是右手四指由 的方向转为
的方向转为 的方向时,大拇指所指的方向规定为
的方向时,大拇指所指的方向规定为 ×
× 的方向,
的方向, ×
× =-
=- ×
× 。
。
设 =(x1,y1,z1),
=(x1,y1,z1), =(x2,y2,z2),则
=(x2,y2,z2),则 ×
× =
=

(注:1、二阶行列式: ;2、适合右手定则。)
;2、适合右手定则。)

 Code
Code
 public double[] GetTriangleFunction(ESRI.ArcGIS.Geometry.IPoint point1, ESRI.ArcGIS.Geometry.IPoint point2, ESRI.ArcGIS.Geometry.IPoint point3)
public double[] GetTriangleFunction(ESRI.ArcGIS.Geometry.IPoint point1, ESRI.ArcGIS.Geometry.IPoint point2, ESRI.ArcGIS.Geometry.IPoint point3)


 {
{
 try
try


 {
{
 double a = 0, b = 0,c=0; //方程参数
double a = 0, b = 0,c=0; //方程参数
 double x1 = 0, x2 = 0, x3 = 0, y1 = 0, y2 = 0, y3 = 0, z1 = 0, z2 = 0, z3 = 0; //各点坐标值
double x1 = 0, x2 = 0, x3 = 0, y1 = 0, y2 = 0, y3 = 0, z1 = 0, z2 = 0, z3 = 0; //各点坐标值
 double[] returnValue = new double[3];
double[] returnValue = new double[3];

 x1 = point1.X * 1000;
x1 = point1.X * 1000;
 y1 = point1.Y * 1000;
y1 = point1.Y * 1000;
 z1 = point1.Z * 1000;
z1 = point1.Z * 1000;

 x2 = point2.X * 1000;
x2 = point2.X * 1000;
 y2 = point2.Y * 1000;
y2 = point2.Y * 1000;
 z2 = point2.Z * 1000;
z2 = point2.Z * 1000;

 x3 = point3.X * 1000;
x3 = point3.X * 1000;
 y3 = point3.Y * 1000;
y3 = point3.Y * 1000;
 z3 = point3.Z * 1000;
z3 = point3.Z * 1000;

 //向量I1
//向量I1
 double[] I1 = new double[3];
double[] I1 = new double[3];
 I1[0] = x2 - x1;
I1[0] = x2 - x1;
 I1[1] = y2 - y1;
I1[1] = y2 - y1;
 I1[2] = z2 - z1;
I1[2] = z2 - z1;
 //向量I2
//向量I2
 double[] I2 = new double[3];
double[] I2 = new double[3];
 I2[0] = x3 - x1;
I2[0] = x3 - x1;
 I2[1] = y3 - y1;
I2[1] = y3 - y1;
 I2[2] = z3 - z1;
I2[2] = z3 - z1;

 double X1 = I1[0];
double X1 = I1[0];
 double Y1 = I1[1];
double Y1 = I1[1];
 double Z1 = I1[2];
double Z1 = I1[2];
 double X2 = I2[0];
double X2 = I2[0];
 double Y2 = I2[1];
double Y2 = I2[1];
 double Z2 = I2[2];
double Z2 = I2[2];

 a = Y1 * Z2 - Y2 * Z1;
a = Y1 * Z2 - Y2 * Z1;
 b = X2 * Z1 - X1 * Z2;
b = X2 * Z1 - X1 * Z2;
 c = X1 * Y2 - X2 * Y1;
c = X1 * Y2 - X2 * Y1;


 returnValue[0] = a;
returnValue[0] = a;
 returnValue[1] = b;
returnValue[1] = b;
 returnValue[2] = c;
returnValue[2] = c;

 return returnValue;
return returnValue;
 }
}
 catch (Exception e)
catch (Exception e)


 {
{
 throw e;
throw e;
 }
}

 }
}
![]() ,那么向量
,那么向量叫做平面
的法向量。平面
的法向量共有两大类(从方向上分),无数条。
的法向量
![]() =(x,y,1)[或
=(x,y,1)[或![]() =(x,1,z)或
=(x,1,z)或![]() =(1,y,z)],在平面
=(1,y,z)],在平面内任找两个不共线的向量
,
![]() 。由
。由![]()
,得
![]() ·
·=0且
![]() ·
·![]() =0,由此得到关于x,y的方程组,解此方程组即可得到
=0,由此得到关于x,y的方程组,解此方程组即可得到![]() 。
。![]() =(A,B,C);若平面与3个坐标轴的交点为P(a,0,0),P(0,b,0),P(0,0,c),则平面方程为:
=(A,B,C);若平面与3个坐标轴的交点为P(a,0,0),P(0,b,0),P(0,0,c),则平面方程为:![]() ,称此方程为平面的截距式方程,把它化为一般式即可求出它的法向量。
,称此方程为平面的截距式方程,把它化为一般式即可求出它的法向量。,
![]() 为空间中两个不平行的非零向量,其外积
为空间中两个不平行的非零向量,其外积×
![]() 为一长度等于|
为一长度等于|||
![]() |sinθ,(θ为
|sinθ,(θ为
![]() 两者交角,且0<θ<π,而与
两者交角,且0<θ<π,而与,
![]() ,
,的方向转为
![]() 的方向时,大拇指所指的方向规定为
的方向时,大拇指所指的方向规定为×
![]() 的方向,
的方向,×
![]() =-
=-![]() ×
×。
=(x1,y1,z1),
![]() =(x2,y2,z2),则
=(x2,y2,z2),则×
![]() =
=
![]() ;2、适合右手定则。)
;2、适合右手定则。)








 }
} }
}
 浙公网安备 33010602011771号
浙公网安备 33010602011771号