c++踩方格-动态规划基础题

有一个方格矩阵，矩阵边界在无穷远处。我们做如下假设：
a、每走一步时，只能从当前方格移动一格，走到某个相邻的方格上；
b、走过的格子立即塌陷无法再走第二次；
c、只能向北、东、西三个方向走；
请问：如果允许在方格矩阵上走n步，共有多少种不同的方案。2种走法只要有一步不一样，即被认为是不同的方案。
输入格式
允许在方格上行走的步数n(n≤20)。
输出格式
计算出的方案数量。
样例：1->3；2->7；3->17。

这道题在最初找第三步的时候，只找到15条，一直很懵逼，怎么网上答案都是17条。后来才发现是我漏了，漏的是和2->3和0->1的路线中3和1重叠，将那个3砍掉了。

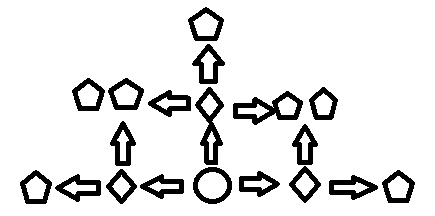
这是第二步的路线图，圆形是起点，四边形是第一步的落点，五边形是第二步的落点。
实际上到了第二步，大概的一个关系能够确定，

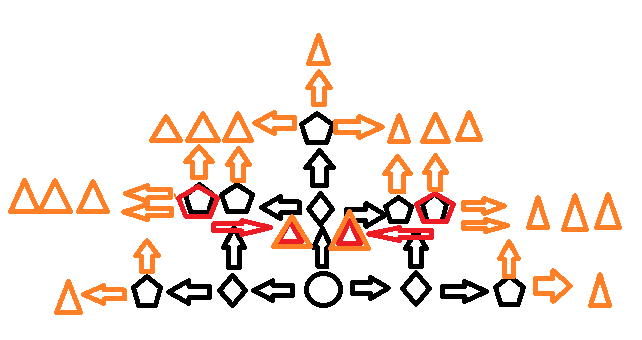
这是第三步的路线图，三角形是第三步的落点，主要是红色标识的地方，这两个三角形，由于路线不同，不会出现坍塌，要计入的。
接下来就是分析关系了。
初始状态F[0]=1，
走了一步后F[1]=3,
走了两步后F[2]=7，
走了三步后F[3]=17。

走第二步的时候，能够发现所有菱形都至少产生了两个方向的五边形，其中一个菱形产生了三个方向的五边形。F[2]=32+1
走第三步的时候，能够发现所有菱形都至少产生了两个方向的三角形，而有三处菱形产生了三个方向的五边形。F[3]=72+3
根据画图，能够发现，上一步的基础上，向上和向左（或者向右）都是存在的，有2F[i-1]。那么多出来的向左（或者向右）是由哪部分产生？
是上上一步的向上箭头产生的图形，才拥有多朝左（或者右）的分支。
比如红圈圈出来的五边形以及顶部的五边形，都是菱形向上箭头产生出来的，而他们都拥有三个分支。往前看，第二步中菱形有三个分支的那处，也是向上箭头产生的。如果对于数据还是不够确定规律，可以继续画第四步，进行验证。

#include<bits/stdc++.h>
using namespace std;
int main(){
    int f[21]={1, 3, 7, 17}, n;
    cin >> n;
    for(int i=3;i<=n;i++){
        f[i]=2*f[i-1]+f[i-2];
    }
    cout << f[n] << endl;
    return 0;
}

递归写法

#include<bits/stdc++.h>
using namespace std;

int dfs(int n){
	if(n<1) return 1;
	if(n==1) return 3;
	if(n==2) return 7;
	return 2*dfs(n-1)+dfs(n-2);
}

int main(){
	int n;
	cin >> n;
	cout << dfs(n) << endl;
	return 0;
}

上面那种递归，dfs(2)至少会进入两次，所以可以记忆化搜索

#include <bits/stdc++.h>
using namespace std;

int dp[21] = {1, 3, 7};

int dfs(int n) {
	if (n < 1) return 1;
	if (n == 1) return 3;
	if (n == 2) return 7;
	if (dp[n - 1] == 0)  dp[n - 1] = dfs(n - 1);
	if (dp[n - 2] == 0)  dp[n - 2] = dfs(n - 2);
	return 2 * dp[n - 1] + dp[n - 2];
}

int main() {
	int n;
	cin >> n;
	cout << dfs(n) << endl;
	return 0;
}

总的来说，肯定还是第一种使用数组存储更便捷。