数据结构—完全二叉树
上篇博客介绍了一种非线性结构—普通树 的含义以及一些特性,本文将介绍二叉树、满二叉树以及完全二叉树的一些特性及实现。
首先,什么是二叉树?
二叉树,是度为二的树,二叉树的每一个节点最多只有二个子节点,且两个子节点有序。
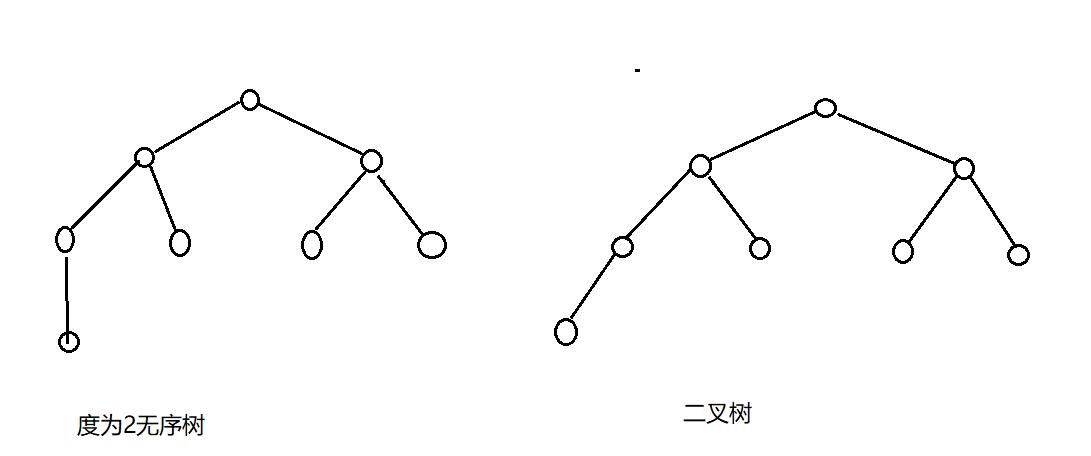
二叉树的重要特性:
1.二叉树的第i层上节点数最多2n-1。
2.高度为k的二叉树中,最多有2k-1个节点。
3.在任意一棵二叉树中,如果终端节点的度为n,度为2的节点数为m,则n=m+1。
4.二叉树的子树有左右之分,顺序不能颠倒。
5.若采用连续储存的方式存放二叉树,则节点下标之间的关系:
若某个节点的下标为 i ,则这个节点的父节点的下标为 i / 2。
若某个节点下标为 i ,且节点的度为2,则这个节点的左子节点的下标为 2 * i + 1 ,右子节点的下标为 2 * i + 2 。
满二叉树:树最后一层没有任何子节点,其余每一层的所有节点都有2个子节点。
满二叉树的性质:
1.满二叉树的第i层的节点数为2n-1个。
2.深度为k的满二叉树必有2k-1个节点 ,叶子数为2k-1。
3.满二叉树中不存在度为1的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
4.具有n个节点的满二叉树的深度为log2(n+1)。
完全二叉树:如果二叉树的深度为k,则除第k层外其余所有层节点的度都为2,且叶子节点从左到右依次存在。也即是,将满二叉树的最后一层从左到右依次删除若干节点就得到完全二叉树。满二叉树是一棵特殊的完全二叉树,但完全二叉树不一定是满二叉树。
完全二叉树的性质:
1.满二叉树是一棵特殊的完全二叉树,但完全二叉树不一定是满二叉树。
2.在满二叉树中最下一层,连续删除若干个节点得到完全二叉树。
3.在完全二叉树中,若某个节点没有左子树,则一定没有有子树。
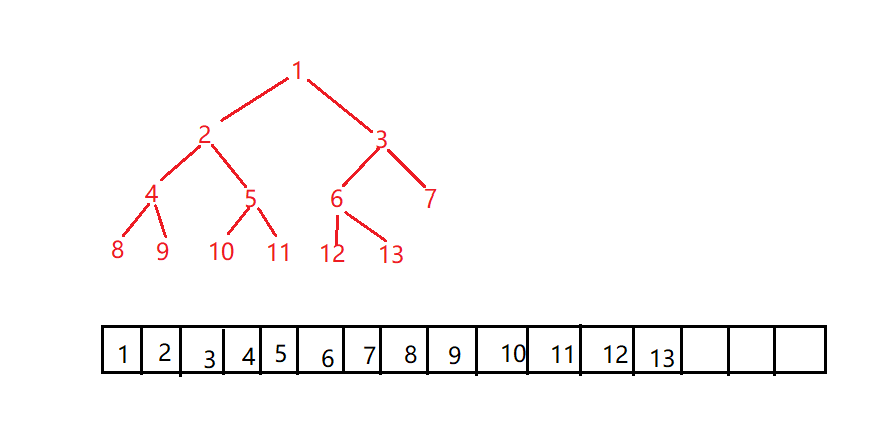
4.若采用连续储存的方式存放二叉树,则节点下标之间的关系(根节点下标为0):
若某个节点的下标为 i ,则这个节点的父节点的下标为 i / 2。
若某个节点下标为 i ,且节点的度为2,则这个节点的左子节点的下标为 2 * i + 1 ,右子节点的下标为 2 * i + 2 。
除了根节点外,左子树的下标为基数,右子树的下标为偶数。
[ MyBinaryTree.h ]
1 /**********************************************
2 完全二叉树类模板 树组实现
3 2018/3/22
4 /**********************************************/
5
6
7 #pragma once
8 using namespace std;
9 #include "stdafx.h"
10 #include <iostream>
11
12 template<class T>
13 class MyBinaryTree
14 {
15 private:
16 T *pRoot; //采用动态数组存储
17 size_t len;
18 size_t maxSize;
19
20 void _sizeExpand();
21 int _find(const T& val); //在树中查找元素并返回他在容器中的下标 ,若没找到返回-1;
22
23 public:
24 MyBinaryTree();
25 ~MyBinaryTree();
26 void clear(); //清空二叉树
27 void appand(const T& val); //在完全二叉树尾部追加数据
28 T& find(const T& findVal); //在树中查找元素并返回钙元素的引用
29 bool isFind(const T& findVal);
30 void initTree(const T arr[], size_t n); //传入一个数组 初始化树
31 T& getParent(const T& val);
32 T& getLef/Child(const T& val);
33 T& getRightChild(const T& val);
34
35 void prePrint(int index = 0);
36 void posPrint(int index = 0);
37 void inPrint(int index = 0);
38
39
40 };
41
42 template<class T>
43 void MyBinaryTree<T>::inPrint(int index /*= 0*/)
44 {
45 if (index < (int)len&&index >= 0)
46 {
47 inPrint(2 * index + 1);
48 cout << pRoot[index] << " ";
49 inPrint(2 * index + 2);
50 }
51 }
52
53 template<class T>
54 void MyBinaryTree<T>::posPrint(int index /* = 0*/)
55 {
56 if (index < (int)len&&index >= 0)
57 {
58 posPrint(2 * index + 1);
59 posPrint(2 * index + 2);
60 cout << pRoot[index] << " " ;
61 }
62 }
63
64 template<class T>
65 void MyBinaryTree<T>::prePrint(int index /* = 0*/)
66 {
67 if (index < (int)len&&index >= 0)
68 {
69 cout << pRoot[index]<<" ";
70 prePrint(2 * index + 1);
71 prePrint(2 * index + 2);
72 }
73 }
74
75 template<class T>
76 T& MyBinaryTree<T>::getRightChild(const T& val)
77 {
78 int temp = _find(val);
79 if (temp == -1 || 2 * temp + 2 >= len) //没有找到元素,或者没有右子树
80 {
81 throw"the data has no rightchild";
82 }
83 return pRoot[2 * temp + 2];
84 }
85
86 template<class T>
87 T& MyBinaryTree<T>::getLeftChild(const T& val)
88 {
89 int temp = _find(val);
90 if (temp == -1 || 2 * temp + 1 >= len) //没有找到元素,或者没有左子树
91 {
92 throw"the data has no leftchild";
93 }
94 return pRoot[2 * temp + 1];
95 }
96
97 template<class T>
98 T& MyBinaryTree<T>::getParent(const T& val)
99 {
100 int temp=_find(val);
101 if (temp == 0) //返回0,表示val为根节点 ,没有父亲
102 cout << "该节点为根节点,没有父亲" << endl;
103 return -1;
104 if (temp == -1) //没有找到数据val
105 throw "the data is not in zhe tree";
106 else
107 return pRoot[(temp - 1) >> 1 ]108 }
109
110 template<class T>
111 void MyBinaryTree<T>::initTree(const T arr[], size_t n)
112 {
113 clear(); //初始化之前先 判断树是否为空 若不是,则先清空
114 len = n;
115 maxSize = n;
116 pRoot = new T[maxSize];
117 memcpy_s(pRoot, len*sizeof(T), arr, len*sizeof(T));
118
119 // for (size_t i = 0; i < n; i++)
120 // { //循环效率太低,直接内存拷贝
121 // //_sizeExpand(); 效率低 指直接一次性申请内存 //插入数据之前 先判断容器是否已满
122 // pRoot[i] = arr[i];
123 // len++;
124 // }
125 }
126
127 template<class T>
128 int MyBinaryTree<T>::_find(const T& val)
129 {
130 for (int i = 0; i < len;++i)
131 {
132 if (public[i] == val)
133 return i;
134 }
135 return -1;
136 }
137
138
139 template<class T>
140 bool MyBinaryTree<T>::isFind(const T& findVal)
141 {
142 return _find(findVal)!=-1;
143 }
144
145 template<class T>
146 T& MyBinaryTree<T>::find(const T& findVal)
147 {
148 int tempIndex = _find(findVal);
149 if (tempIndex != -1)
150 return pRoot[tempIndex];
151 else
152 throw "can not find the data";
153 }
154
155 template<class T>
156 void MyBinaryTree<T>::_sizeExpand()
157 {//只扩充容量 容器没存满是不扩充
158 if (len>=maxSize)
159 {
160 maxSize = maxSize +(( maxSize / 2 > 1) ? maxSize / 2 : 1);
161 T *temp = new T[maxSize];
162 if (pRoot)
163 {
164 memcpy_s(temp, len*sizeof(T), pRoot, len*sizeof(T));
165 delete[]pRoot;
166 pRoot = temp;
167 }
168 }
169 }
170
171 template<class T>
172 void MyBinaryTree<T>::appand(const T& val)
173 {
174 _sizeExpand();
175 pRoot[len++] = val;
176 }
177
178 template<class T>
179 void MyBinaryTree<T>::clear()
180 {
181 if (pRoot) //若树为非空 删除内存空间
182 delete[]pRoot;
183 pRoot = NULL;
184 len = maxSize = 0;
185 }
186
187 template<class T>
188 MyBinaryTree<T>::~MyBinaryTree()
189 {
190 clear();
191 }
192
193 template<class T>
194 MyBinaryTree<T>::MyBinaryTree()
195 {
196 pRoot = NULL;
197 len = maxSize = 0;
198 }
代码测试:
1 // 完全二叉树.cpp : 定义控制台应用程序的入口点。
2 //
3
4 #include "stdafx.h"
5 #include "MyBinaryTree.h"
6 #include <iostream>
7
8 using namespace std;
9
10 int _tmain(int argc, _TCHAR* argv[])
11 {
12 MyBinaryTree<int> tree;
13 int arr[10];
14 for (int i = 0; i < 10; ++i)
15 arr[i] = i;
16 cout << "完全二叉树初始化并遍历打印" << endl;
17 tree.initTree(arr, 10);
18 cout << "前序遍历: " ;
19 tree.prePrint(); cout << endl;
20 cout << "中序遍历: ";
21 tree.inPrint(); cout << endl;
22 cout << "后序遍历: " ;
23 tree.posPrint(); cout << endl;
24 cout << "----------------------------------" << endl;
25
26 cout << "在树的叶节点增加数据:" << endl;
27 tree.appand(10);
28 tree.appand(11);
29 tree.prePrint(); cout << endl;
30 tree.appand(12);
31 tree.appand(13);
32 tree.prePrint(); cout << endl;
33 cout << "----------------------------------" << endl;
34
35 cout << "获得父节点、左右子节点:" << endl;
36 cout << "4的父节点:" << tree.getParent(4) << endl;
37 cout << "4的左子节点:" << tree.getLeftChild(4) << endl;
38 cout << "4的右子节点:" << tree.getRightChild(4) << endl;
39
40
41
42
43 cin.get();
44 return 0;
45 }
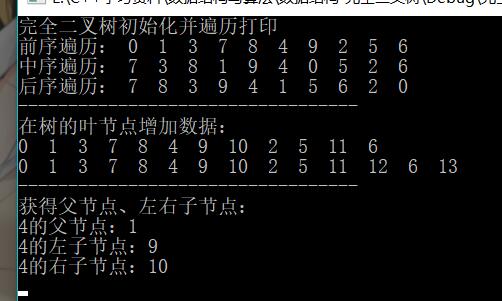
运行结果:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号