24.12.11
实验六:朴素贝叶斯算法实现与测试
一、实验目的
深入理解朴素贝叶斯的算法原理,能够使用Python语言实现朴素贝叶斯的训练与测试, 并且使用五折交叉验证算法进行模型训练与评估。
二、实验内容
(1)从scikit-learn 库中加载 iris 数据集,使用留出法留出 1/3 的样本作为测试集(注 意同分布取样);
(2)使用训练集训练朴素贝叶斯分类算法;
(3)使用五折交叉验证对模型性能(准确度、精度、召回率和 F1 值)进行评估和选 择;
(4)使用测试集,测试模型的性能,对测试结果进行分析,完成实验报告中实验六的 部分。
三、算法步骤、代码、及结果
1. 算法伪代码
# 1. 加载数据集
加载 iris 数据集
X, y = 加载数据集() # 特征数据和标签数据
# 2. 数据分割
X_train, X_test, y_train, y_test = 划分数据集(X, y, test_size=1/3, stratify=y)
# 3. 初始化朴素贝叶斯分类器
分类器 = 高斯朴素贝叶斯()
# 4. 训练模型
训练模型(分类器, X_train, y_train)
# 5. 使用五折交叉验证评估模型
交叉验证结果 = 五折交叉验证(分类器, X, y)
准确度 = 计算准确度(交叉验证结果)
精度 = 计算精度(交叉验证结果)
召回率 = 计算召回率(交叉验证结果)
F1值 = 计算F1值(交叉验证结果)
输出("五折交叉验证结果:")
输出(准确度)
输出(精度)
输出(召回率)
输出(F1值)
# 6. 使用测试集评估模型
y_pred = 预测标签(分类器, X_test)
测试集准确度 = 计算准确度(y_test, y_pred)
测试集精度 = 计算精度(y_test, y_pred)
测试集召回率 = 计算召回率(y_test, y_pred)
测试集F1值 = 计算F1值(y_test, y_pred)
输出("测试集性能:")
输出(测试集准确度)
输出(测试集精度)
输出(测试集召回率)
输出(测试集F1值)
2. 算法主要代码
完整源代码\调用库方法(函数参数说明)
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import cross_val_score
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
# 加载 iris 数据集
iris = load_iris()
X, y = iris.data, iris.target
# 留出法分割数据集,1/3 用作测试集,2/3 用作训练集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=1/3, stratify=y, random_state=42)
# 初始化高斯朴素贝叶斯分类器
naive_bayes = GaussianNB()
# 在训练集上训练模型
naive_bayes.fit(X_train, y_train)
# 使用五折交叉验证评估模型性能
cv_accuracy = cross_val_score(naive_bayes, X, y, cv=5, scoring='accuracy')
cv_precision = cross_val_score(naive_bayes, X, y, cv=5, scoring='precision_weighted')
cv_recall = cross_val_score(naive_bayes, X, y, cv=5, scoring='recall_weighted')
cv_f1 = cross_val_score(naive_bayes, X, y, cv=5, scoring='f1_weighted')
# 输出五折交叉验证结果
print("五折交叉验证结果:")
print(f"准确度:{cv_accuracy.mean():.4f}")
print(f"精度:{cv_precision.mean():.4f}")
print(f"召回率:{cv_recall.mean():.4f}")
print(f"F1值:{cv_f1.mean():.4f}")
# 使用测试集评估模型
y_pred = naive_bayes.predict(X_test)
# 计算测试集的性能指标
test_accuracy = accuracy_score(y_test, y_pred)
test_precision = precision_score(y_test, y_pred, average='weighted')
test_recall = recall_score(y_test, y_pred, average='weighted')
test_f1 = f1_score(y_test, y_pred, average='weighted')
# 输出测试集性能
print("\n测试集性能:")
print(f"准确度:{test_accuracy:.4f}")
print(f"精度:{test_precision:.4f}")
print(f"召回率:{test_recall:.4f}")
print(f"F1值:{test_f1:.4f}")
1. GaussianNB (高斯朴素贝叶斯)
用于连续特征的数据,假设特征服从正态分布。
主要参数:
• priors
o 意义:类别的先验概率分布。
o 取值:数组类型,长度与类别数相同。
o 默认值:None,即模型会根据数据自动计算类别的先验概率。
• var_smoothing
o 意义:为避免数值稳定性问题,在计算过程中加入一个很小的平滑参数到所有特征的方差中。
o 取值:正数,通常为一个非常小的值(如 1e-9)。
o 默认值:1e-9。
________________________________________
2. MultinomialNB (多项式朴素贝叶斯)
适用于离散数据(例如文档分类)。
主要参数:
• alpha
o 意义:平滑参数(Laplacian/Lidstone 平滑)。用于防止概率为 0 的情况。
o 取值:正数,推荐使用较小的值(如 1.0 或 0.01)。
o 默认值:1.0。
• fit_prior
o 意义:是否学习类别的先验概率。
o 取值:布尔值(True 或 False)。
True:根据训练数据估计类别先验概率。
False:所有类别的先验概率设置为相等。
o 默认值:True。
• class_prior
o 意义:手动设置类别的先验概率。
o 取值:数组类型,长度与类别数相同。
o 默认值:None,即模型会自动计算。
________________________________________
3. BernoulliNB (伯努利朴素贝叶斯)
用于二元特征(0/1)。
主要参数:
• alpha
o 意义:平滑参数,用于防止某些特征概率为 0。
o 取值:正数,推荐使用较小值(如 1.0 或 0.01)。
o 默认值:1.0。
• binarize
o 意义:将特征值阈值化为二进制值。例如,binarize=0.0 将特征值 > 0 转化为 1,否则为 0。
o 取值:浮点数或 None。
None:数据不会被二值化。
浮点数:作为阈值进行二值化。
o 默认值:0.0。
• fit_prior
o 意义:是否学习类别的先验概率。
o 取值:布尔值(True 或 False)。
True:根据数据计算先验概率。
False:所有类别的先验概率均等。
o 默认值:True。
• class_prior
o 意义:手动设置类别的先验概率。
o 取值:数组类型,长度与类别数相同。
o 默认值:None,表示自动计算。
cross_val_score(用于交叉验证)
主要参数:
• estimator
o 意义:指定用于评估的模型。
o 取值:任何符合 scikit-learn 估计器接口的模型。
• X 和 y
o 意义:特征矩阵和目标变量。
o 取值:
X:形状为 [n_samples, n_features] 的二维数组。
y:形状为 [n_samples] 的一维数组。
• cv
o 意义:决定交叉验证拆分的策略。
o 取值:整数或交叉验证生成器对象。
整数:指定折数(如 5 表示五折交叉验证)。
交叉验证生成器:例如 KFold、StratifiedKFold。
o 默认值:None(默认使用 5 折交叉验证)。
• scoring
o 意义:指定评估指标。
o 取值:字符串或可调用对象。
常用值:'accuracy'、'precision_weighted'、'recall_weighted'、'f1_weighted' 等。
o 默认值:None(使用模型的默认评分指标)。
3. 训练结果截图(包括:准确率、精度(查准率)、召回率(查全率)、F1)
四、实验结果分析
1. 测试结果截图(包括:准确率、精度(查准率)、召回率(查全率)、F1)
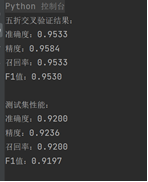
2. 对比分析
性能差异:五折交叉验证的性能整体优于测试集性能,这表明模型在训练数据上的表现较为理想。测试集性能略低,说明模型可能存在轻微的过拟合,导致对新数据的泛化能力稍差。
模型优势: 朴素贝叶斯分类器在高维小样本情况下表现较好,且计算效率高。从上述指标来看,模型对数据分布变化具有一定健壮性,但在更复杂或具有较多噪声的测试集上,其性能可能会下降。