Coding the Matrix (0):映射、复数和域
1. 非常好的 Python 教程
《深入 Python 3.0》 以及 IBM 开发社区的博客探索 Python .
2. 子集: s 是 S 的子集
>>>S = {2, 3, 4, 5, 6, 7}
>>>s = {x for x in S if x%2==0} # 偶数子集
>>>s
set([2, 4, 6])
3. 映射:Ceasar 加密
>>> import string >>> table = string.maketrans("abcdefghijklmnopqrstuvwxyz", "cdefghijklmnopqrstuvwxyzab") # 向后平移两位 >>> print "hello".translate(table) jgnnq
4. 复数练习
>>> 1 + 1j (1+1j) >>> 1 + 1j + (10 + 20j) # 相加 (11+21j) >>> x = 1 + 3j >>> (x - 1)**2 # 相乘 (-9+0j) >>> x.real # 实部 1.0 >>> x.imag # 虚部 3.0 >>> type(x) <type 'complex'>
5. 复平面
-
复数的绝对值
>>> abs(3 + 4j) 5.0![]()
-
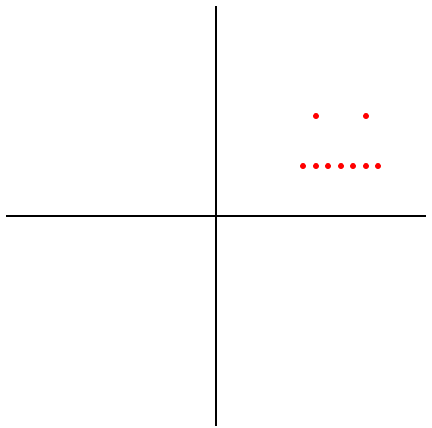
复数画点
plotting.py 的下载地址
>>> from plotting import plot >>> L = [2+2j, 3+2j, 1.75+1j, 2+1j, 2.25+1j, 2.5+1j, 2.75+1j, 3+1j, 3.25+1j] >>> plot(L)
画图如下:
![]()
-
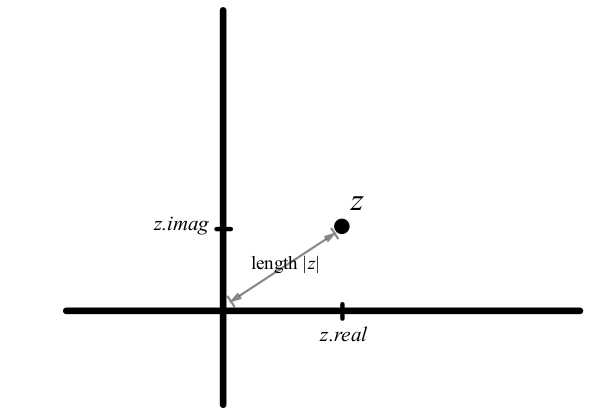
复数画图
>>> from image import * >>> I = color2gray(file2image('./pic/01.png')) >>> row = len(I) # 垂直高度 >>> col = len(I[0]) # 水平长度 >>> M = [x + y*1j for x in range(col) for y in range(row) if I[row-y-1][x] < 120] >>> plot(M, max(row, col), 1) # 第二个参数便于坐标系大小的自动调节, 第三个参数表示每个像素显示的大小
![]()
-
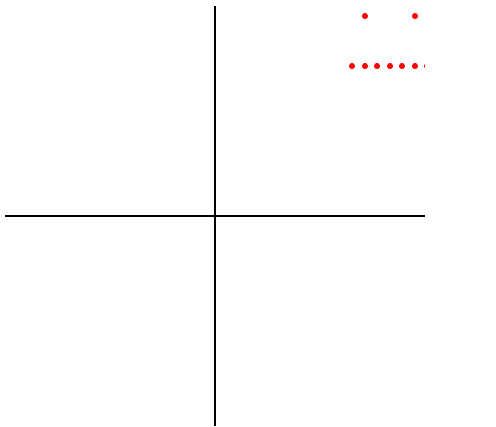
图像平移
(x + yi) to (a+x + (b+y)i)
>>> plot({z + (1+2j) for z in L})![]()
-
图像缩放
(x + yi) to (0.5x + 0.5yi)
>>> plot([.5*z for z in M], max(row, col), 1)
![]()
-
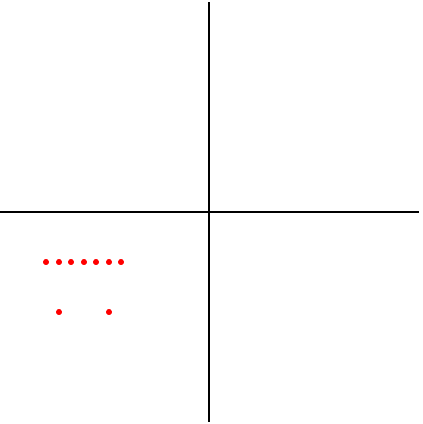
中心对称变换
(x + yi) to (-x - yi)
>>> plot({-z for z in L})![]()
-
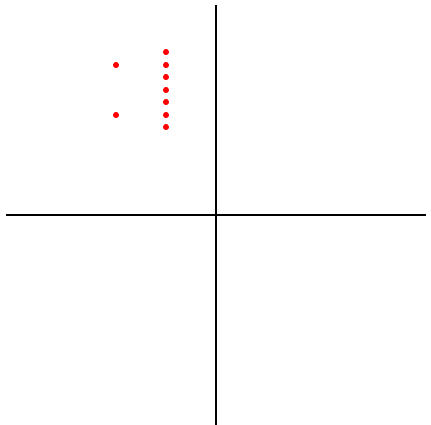
以坐标轴为中心旋转 90 度
(x + yi) to (-y + xi)
the same as:
(x + yi) to i*(x + yi)
>>> plot({1j*z for z in L})![]()
-
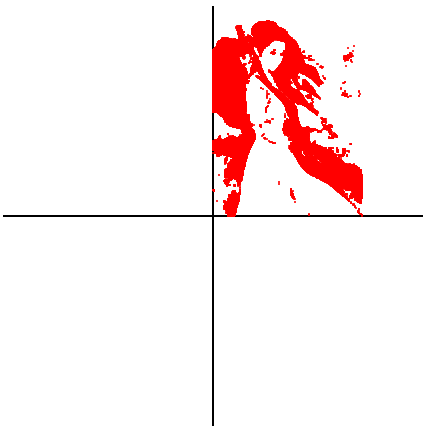
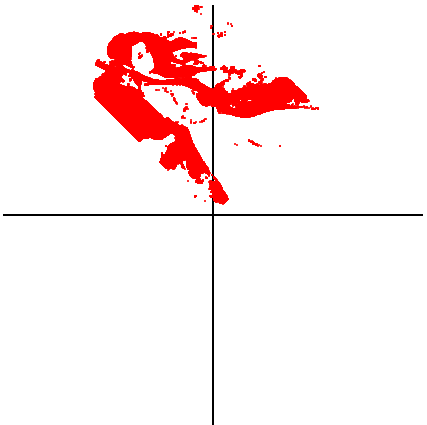
以坐标轴为中心任意旋转和缩放
![]()
旋转 45 度:
>>> from math import pi, e >>> plot([e**(pi*1j/4)*z for z in M], max(row, col), 1)
![]()
欧拉恒等式:
![]() 欧拉公式:
欧拉公式:
![]()
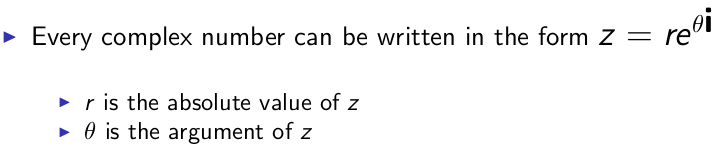
6. Playing with GF(2)
-
玩玩有限域(伽罗华域, galois field)
galois field 2 只有两个元素: 0 和 1. 在这个域中,加法运算是异或操作,乘法运算是与操作。运算律比如分配律在这里仍然适用。
>>> from GF2 import one >>> one + one 0 >>> one + 0 one >>> one * one one >>> one * 0 0 >>> one / one one
对于这样一个加密系统:
![]()
概率均匀分布,并且密文与明文是独立的。
-
Network coding
Streaming video through network
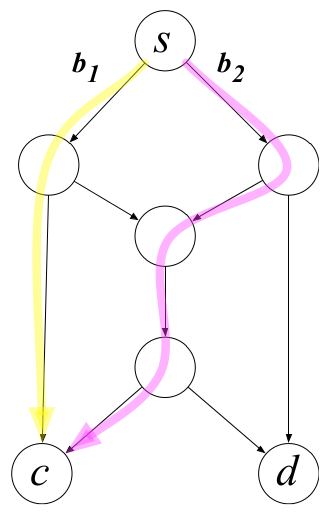
a) 一个顾客木有问题
![]()
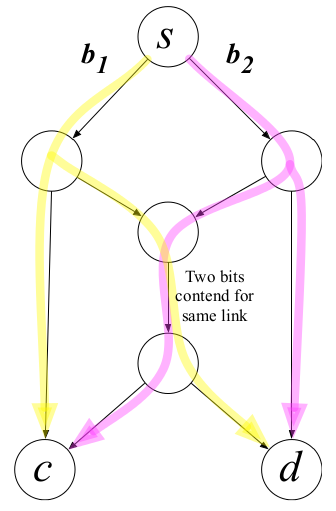
b) 两个顾客发生冲突
![]()
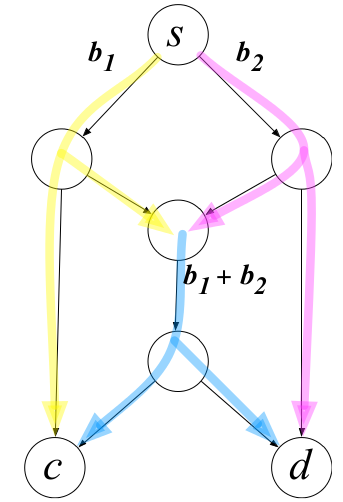
c) 先编码,再解码,两个发送端可同时发送到两个接收端
![]()
掰掰~



 欧拉公式:
欧拉公式: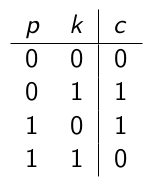


 浙公网安备 33010602011771号
浙公网安备 33010602011771号