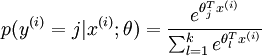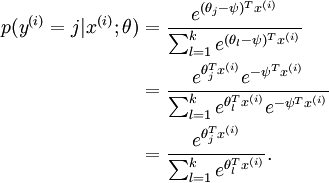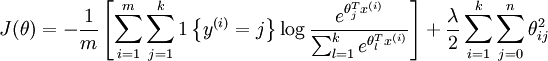Logistic Regression 之基础知识准备

 0. 前言

  这学期 Pattern Recognition 课程的 project 之一是手写数字识别，之二是做一个网站验证码的识别(鸭梨不小哇）。面包要一口一口吃，先尝试把模式识别的经典问题——手写数字识别做出来吧。这系列博客参考 deep learning tutorial ，记录下用以下三种方法的实现过程:

1. Logistic Regression - using Theano for something simple
2. Multilayer perceptron - introduction to layer
3. Deep Convolutional Network - a simplified version of LeNet5

  目的在于一方面从理论上帮自己理顺思路，另一方面作为课程最后一课 presentation 的材料。这三种方法从易到难，准确率也由低到高，我们先从简单的入手。

1. Binomial logistic regression model

  尽管线性分类器方法足够简单并且使用广泛，但是线性模型对于输出的 y 没有界限，y 可以取任意大或者任意小（负数）的值，对于某些问题来说不够 adequate, 比如我们想得到 0 到 1 之间的 probability 输出，这时候就要用到比 linear regression 更加强大的 logistic regression 了。

 y = w • x

  直觉上，一个线性模型的输出值 y 越大，这个事件 P(Y=1|x) 发生的概率就越大。 另一方面，我们可以用事件的几率（odds）来表示事件发生与不发生的比值，假设发生的概率是 p ，那么发生的几率（odds）是 p/(1-p) ， odds 的值域是 0 到正无穷，几率越大，发生的可能性越大。将我们的直觉与几率联系起来的就是下面这个（log odds）或者是 logit 函数 (有点牵强 - -!)：

  进而可以求出概率 p 关于 w 点乘 x 的表示：

  (注：为什么要写出中间一步呢？看到第三部分的你就明白啦!)

  这就是传说中的 sigmoid function 了，以 w 点乘 x 为自变量，函数图像如下:

(注：从图中可以看到 wx 越大，p 值越高，在线性分类器中，一般 wx = 0 是分界面，对应了 logistic regression 中 p = 0.5)

2. Parameter Estimation

  Logsitic regression 输出的是分到每一类的概率，参数估计的方法自然就是最大似然估计 (MLE) 咯。对于训练样本来说，假设每个样本是独立的，输出（标签）为 y = {0, 1}，样本的似然函数就是将所有训练样本 label 对应的输出节点上的概率相乘, 令 p = P(Y=1|x) ,如果 y = 1, 概率就是 p， 如果 y = 0, 概率就是 1 - p ，（好吧，我是个罗嗦的家伙),  将这两种情况合二为一，得到似然函数：

  嗯？有连乘，用对数化为累加， balabala 一通算下来，就得到了对数似然函数为

  应用梯度下降法或者是拟牛顿法对 L(w) 求极大值，就可以得到 w 的估计值了。

3. Softmax regression

  这一小节旨在弄清 softmax regression 和 logistic regression 的联系，更多细节请参考 Andrew Ng 的英文资料，需要快速浏览也可以看看中文翻译版本，或者 wiki 一下。

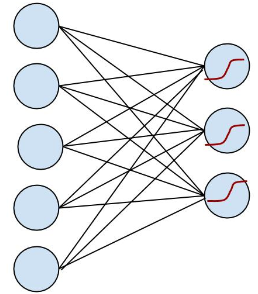
  logistic regression 在多类上的推广又叫 softmax regression， 在数字手写识别中，我们要识别的是十个类别，每次从输入层输入 28×28 个像素，输出层就可以得到本次输入可能为 0, 1, 2… 的概率。得花点时间画个简易版本的，看起来更直观:

  OK, 左边是输入层，输入的 x 通过中间的黑线 w (包含了 bias 项)作用下，得到 w.x, 到达右边节点， 右边节点通过红色的函数将这个值映射成一个概率，预测值就是输入概率最大的节点，这里可能的值是 {0, 1, 2}。在 softmax regression 中，输入的样本属于第 j 类的概率可以写成：

  (注：对比第一部分提到过的中间一步，有什么不同？)   

     注意到，这个回归的参数向量减去一个常数向量，会有什么结果：

  没有变化！这说明如果某一个向量是代价函数的极小值点，那么这个向量在减去一个任意的常数向量也是极小值点，这是因为 softmax 模型被过度参数化了。(题外话：回想一下在线性模型中，同时将 w 和 b 扩大两倍，模型的分界线没有变化，但是模型的输出可信度却增大了两倍，而在训练迭代中， w 和 b 绝对值越来越大，所以 SVM 中就有了函数距离和几何距离的概念)

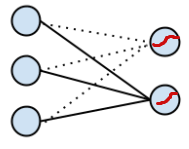
  既然模型被过度参数化了，我们就事先确定一个参数，比如将 w1 替换成全零向量，将 w1.x = 0 带入 binomial softmax regression ，得到了我们最开始的二项 logistic regression (可以动手算一算), 用图就可以表示为

  (注：虚线表示为 0 的权重，在第一张图中没有画出来，可以看到 logistic regression 就是 softmax regression 的一种特殊情况)

  在实际应用中，为了使算法实现更简单清楚，往往保留所有参数，而不任意地将某一参数设置为 0。我们可以对代价函数做一个改动：加入权重衰减 (weight decay)。 权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。并且此时代价函数变成了严格的凸函数， Hessian矩阵变为可逆矩阵，保证有唯一的解。(感觉与线性分类器里限制 ||w|| 或者设置某一个 w 为全零向量一样起到了减参的作用，但是这个计算起来简单清晰，可以用高斯分布的 MAP 来推导，其结果是将 w 软性地限制在超球空间，有一点 “soft” 的味道，个人理解^ ^)

  加入权重衰减后的代价函数是：

  等号右边第一项是训练样本 label 对应的输出节点上的概率的负对数，第二项是 weight decay ，可以使用梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。总结起来，logistic regression 是 softmax regression 的一种特殊形式，前者是二类问题，后者是多类问题，前者的非线性函数的唯一确定的 sigmoid function (默认 label 为 0 的权重为全零向量的推导结果), 后者是 softmax, 有时候我们并不特意把它们区分开来。

      好，基础知识准备完毕，下面我们就要在数字手写识别项目里面实战一下了。(^_^)

  

---

参考资料：

[1] 统计学习方法， 李航 着

[2] http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial