WMD词移距离-计算文档相似度
WMD
Paper: From Word Embeddings To Document Distances
2015年,提出词移距离WMD(Word Mover's Distance):词移距离是在词向量的基础上发展而来的用来衡量文档相似性的度量, 是一种计算句子之间距离的方法,距离越小,相似度越高。
1. 为什么提出?
计算句子/文档相似度的一些方法有:
-
无监督的句子相似度计算——Jaccard相似系数:
Jaccard相似系数用来衡量两个集合之间的相似性,被定义为两个集合交集的元素个数除以并集的元素个数。
\[SIM(s_1,s_2) = \frac{\text{intersection}(words1, words2)}{\text{union}(words1, words2)} \]Jaccard相似系数值越大,句子相似度越高。
Jaccard距离用来度量两个集合之间的差异性,它是Jaccard的相似系数的补集,被定义为1减去Jaccard相似系数。
\[d(s_1,s_2)=1-SIM(s_1,s_2) = 1-\frac{\text{intersection}(words1, words2)}{\text{union}(words1, words2)} \]Jaccard距离越大,句子相似度越小。
-
使用向量空间模型,对句子进行向量表征,再计算两两之间的欧式距离、余弦相似度等度量指标。
基于Word2Vec,使用预先训练好的word-embdding向量,对于一个句子,将词向量的每一位进行加和或求平均。
对句子建模,方法包括skip-gram,cbow的doc2vector建模方法,基于autoencoder的建模方法,基于skip-thought的句子建模方法等。基于sentence-vector的方法能够更好的保留句子的语义信息,能够在一定程度上弥补词袋缺点。
首先解决文档表示,可以通过:
- 词袋(BOW)/TF-IDF:不考虑文法及词的顺序,只考虑词频,将文本进行向量化表示。存在的问题:如果两个句子没有相同词语,根据向量表示会判定为完全不相关,但两者可能具有相同的语义。
- LSI和LDA:将相似词归入主题,文档表示为主题的概率分布。相比BOW更连贯,但不能改善BOW的性能效果。比较两个文档的相似度,可以比较两个文档主题分布的差异。
- Word2Vec:基于word2vec把文本中的所有词映射到一个词向量空间。在一定程度上解决了语义问题,使用CBOW/Skip-Gram考虑上下文信息,词向量可以反映词与词之间的语义差别。再将文档/句子表征为所有词向量的平均,通过计算两两之间的欧式距离、余弦相似度等衡量文档相似度。
Word2Vec考虑词间的距离,提出的WMD是考虑文档间的距离。用一个距离反映文档和文档间的相似度,一个想法:将文档建模成2个文档中词的语义距离的一个组合,比如对两个文档中的任意两个词所对应的词向量求欧式距离然后再加权求和。
2. 如何解决问题?
WMD的求解是EMD问题的一个特例 。
2.1 定义问题
2.1.1 归一化词频
归一化词频(normalized bag-of-words,nBOW),如果一个词\(i\)在文本中出现的次数为\(c_i\),它的归一化词频为:
单词的重要程度与词的出现频率相关(并且归一化)。
2.1.2 词移动代价
词移动代价(Word travel cost),由于WMD中词语是经过word2vec表示的,而word2vec表示后的词可以直接计算欧式距离。单词\(i\)和单词\(j\)的语义距离\(c(i,j)\)为欧式距离:
2.1.3 文档距离
文档距离(Document distance)的直观表示:\(\sum_{i,j}T_{ij}\cdot c(i,j)\)
转移矩阵\(T_{ij}\):文档\(d\)中的单词\(i\)到另一文档\(d'\)中的单词\(j\)的权重。
2.1.4 约束条件
结合EMD这个经典的运输问题(Transportation problem),目标是:最小化两个文档的总距离(移动代价);添加约束条件调整权重:让文档\(d\)中的每个单词都以不同的权重匹配到到另一文档\(d'\)中所有单词。
2.2 快速计算
解决WMD优化问题的最佳平均时间复杂度为\(O(p^3 \log p)\),其中\(p\)表示文档中唯一词的数量。如果数据集有大量的文档或者有大量的唯一词,解决WMD优化问题就很困难。
计算两个文档之间的WMD就要求解一个大型的线性规划问题,如果要用它来做K-NN( k个最相似文档)就比较耗时了,因此提出了了两个优化方案来减小计算量。
论文中提出了两种设置Lower bounds 的方法来过滤文档,通过牺牲部分精准度来减少时间复杂度. 两种方法分别为 Word Centroid Distance( WCD) , Relaxed Word Moving Distance(RWMD)。
2.2.1 WCD
WCD(Word centroid distance),根据三角不等式\(|a|+|b|\ge |a\pm b|\ge ||a|-|b||\),转化为计算WMD的下限——centroid distance:\(\parallel Xd-Xd'\parallel_2\),如下:
两个文档之间的“centroid”距离将会永远比WMD距离要小。
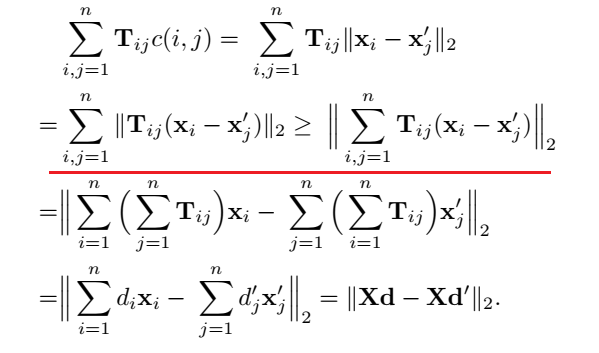
其中\(X\in R^{d\times p}\)是词向量组成的矩阵,算法时间复杂度为\(O(dp)\)。
2.2.2 RWMD
尽管WCD的时间复杂度很低,但是边界过于宽松,无法很好的近似WMD。因此,这里使用更加tight的下界RWMD(Relaxed word moving distance )。RWMD需要计算两次,基于WMD目标函数,分别去掉两个约束条件中的一个,然后求解最小值,使用两个最小值中的最大值作为WMD的近似值。
去掉了一个条件之后,依然符合永远小于原WMD的性质,而以下方程的最优解为,将所有的分配权重都分配到最相近的Euclidean distance的两个单词中。
比如去掉第二个约束条件,得到:

这个问题的最优解为,对于文档\(d\)中的一个词,找到另一个文档\(d'\)中与之最相近的一个词,全部转移到这个词,即:

求得WMD最小值\(l_1(d,d')\)。
同理去掉第一个约束条件,可得:
这个问题的最优解为,对于文档\(d'\)中的一个词,找到另一个文档\(d\)中与之最相近的一个词,全部接收这个词,即:
求得WMD最小值\(l_2(d,d')\)。
最后求\(l_r(d,d')=\max(l_1(d,d'),\;l_2(d,d'))\)结果即为RWMD,时间复杂度为\(O(p^2)\)。
2.2.3 Prefetch and prune 加速k-NN
结合以上两个办法来一起进行剪枝处理。为了找到查询文档\(q\)的k个最近邻,我们可以使用两个下限来大大减少我们需要进行的WMD距离计算量。
K-NN的流程如下:
- 用时间复杂度最小的WCD计算本文档\(q\)与所有文档之间的距离;
- 并将所有文档按照距离从小到大排序;
- 然后只计算前k个文档的WMD距离;
- 遍历剩下的文档,用RWMD计算本文档\(q\)与剩下文档之间的距离,如果距离大于前k个最近文档的WMD距离的最大值,直接剪枝这个文档;如果这个文档的距离小于前k个WMD距离的任何一个,我们就计算这个文档的WMD,并更新k个近邻的文档。
通过这个办法,我们可以剪枝掉95%以上的数据集,非常有效。
3. 优点?
- 效果出色:充分利用了word2vec的领域迁移能力
- 无监督:不依赖标注数据,没有冷启动问题
- 模型简单:仅需要词向量的结果作为输入,没有任何超参数
- 可解释性:将问题转化成线性规划,有全局最优解
- 灵活性:可以人为干预词的重要性
- 检索准确率高
4. 缺点?改进方向?
4.1 缺点
缺点:
- 没有保留语序信息,WMD认为“屡战屡败”和“屡败屡战”在语义上完全一致。
- 不能很好地处理OOV问题:由于词向量是离线训练的,应用于在线业务时会遇到OOV问题,用户query分出来的词,有可能找不到对应的词向量。
- 处理否定词能力差:在训练好的词向量中,通常语义相反的词的词向量是比较相近的,这会导致语义相反的两个句子WMD距离很近。 (很多相似度计算方法的缺点 )
4.2 改进算法S-WMD
WMD距离,学习这个权重矩阵用于聚类(K-NN,那些文档比较相近)的效果很好,但是用来分类的效果很差。
因为一些文章虽然近义词很多, 但是表达的不是一个语义和主题. 比如: I love playing football 和 I like playing piano。虽然看起来句式差不多,可能会归为同类,但是如果打标签时如果是”运动”和”艺术”两类,显然就不能用WMD直接分类了。因为,**WMD没有加入 football和”运动” 是强相关的信息。
论文“Supervised Word Mover’s Distance”提出的WMD算法改进:可训练的加惩罚项的S-WMD。
论文给出的解决方案就是在WMD距离中加入可以训练类别权重的功能:
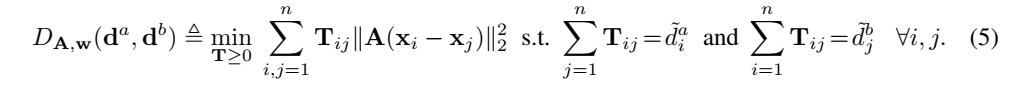
这里的\(d_i\)加入了类别权重\(w_i\):

单词间距离也要进行调整(单词间距离也因为类别不同需要调整距离),加入训练参数矩阵A。

改进方向:
- 可解释性
- 加惩罚项
5. WMD应用
WMD应用:
- 作为特征输入:一个无监督的语义相似度特征。
- 计算文本间距离。
6. WMD代码实现
WMD代码实现的几个要点:
- 找最近的词,
- 优化:处理权重
- 剪枝:topk个文档的排序
目前开源的WMD实现有:
7. 参考
Code:https://github.com/mkusner/wmd
https://zhuanlan.zhihu.com/p/84809907
https://blog.csdn.net/weixin_40547993/article/details/89475630



