算法

https://www.cnblogs.com/alex3714/p/5474411.html

1、冒泡排序 

冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。

它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端，故名。

# 将一组数字，按从小到大排序

import random


def bubble_sort(array):
    for i in range(len(array)):
        for j in range(len(array)-1-i,):
            if array[j] > array[j+1]:
                tmp = array[j]
                array[j] = array[j+1]
                array[j+1] = tmp
　　　　　　　　　 # 以上三句可写为 array[j], array[j + 1] = array[j + 1], array[j]

if __name__ == '__main__': array = [] for i in range(50): array.append(random.randrange(1000)) print(array) bubble_sort(array) print(array)

2、选择排序 

该算法选择最小的未排序项，然后将其与下一个要填充的项进行交换。

选择排序的工作方式如下:在整个数组中查找最小的元素，一旦找到它，就将它(最小的元素)与数组的第一个元素交换。然后查找剩余数组中的最小元素(没有第一个元素的数组)，并将其与第二个元素交换。然后查找剩余数组中的最小元素(没有第一和第二元素的数组)，并将其与第三个元素交换，依此类推

正常版

# 将一组数字中，按从小到大排序

import random


def selection_sort(array):
    for i in range(len(array)):
        for j in range(i, len(array)):
            if array[i] > array[j]:
                array[i], array[j] = array[j], array[i]


if __name__ == '__main__':

    array = []

    for i in range(50):
        array.append(random.randrange(1000))

    print(array)

    selection_sort(array)

    print(array)

优化版

# 将一组数字中，按从小到大排序

import random


def selection_sort(array):
    for i in range(len(array)):
        small_index = i
        for j in range(i, len(array)):
            if array[small_index] > array[j]:
                small_index = j
                array[i], array[small_index] = array[small_index], array[i]


if __name__ == '__main__':

    array = []

    for i in range(5000000):
        array.append(random.randrange(1000))

    print(array)

    selection_sort(array)

    print(array)

插入排序

插入排序(Insertion Sort)的基本思想是：将列表分为2部分，左边为排序好的部分，右边为未排序的部分，循环整个列表，每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子序列中的适当位置，直到全部记录插入完成为止。

插入排序非常类似于整扑克牌。

在开始摸牌时，左手是空的，牌面朝下放在桌上。接着，一次从桌上摸起一张牌，并将它插入到左手一把牌中的正确位置上。为了找到这张牌的正确位置，要将它与手中已有的牌从右到左地进行比较。无论什么时候，左手中的牌都是排好序的。

也许你没有意识到，但其实你的思考过程是这样的：现在抓到一张7，把它和手里的牌从右到左依次比较，7比10小，应该再往左插，7比5大，好，就插这里。为什么比较了10和5就可以确定7的位置？为什么不用再比较左边的4和2呢？因为这里有一个重要的前提：手里的牌已经是排好序的。现在我插了7之后，手里的牌仍然是排好序的，下次再抓到的牌还可以用这个方法插入。编程对一个数组进行插入排序也是同样道理，但和插入扑克牌有一点不同，不可能在两个相邻的存储单元之间再插入一个单元，因此要将插入点之后的数据依次往后移动一个单元。

source = [92, 77, 67, 8, 6, 84, 55, 85, 43, 67]
  
  
for index in range(1,len(source)):
    current_val = source[index] #先记下来每次大循环走到的第几个元素的值
    position = index
  
    while position > 0 and source[position-1] > current_val: #当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
        source[position] = source[position-1] #把左边的一个元素往右移一位
        position -= 1 #只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止
  
    source[position] = current_val #已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
    print(source)

结果：

[77, 92, 67, 8, 6, 84, 55, 85, 43, 67]
[67, 77, 92, 8, 6, 84, 55, 85, 43, 67]
[8, 67, 77, 92, 6, 84, 55, 85, 43, 67]
[6, 8, 67, 77, 92, 84, 55, 85, 43, 67]
[6, 8, 67, 77, 84, 92, 55, 85, 43, 67]
[6, 8, 55, 67, 77, 84, 92, 85, 43, 67]
[6, 8, 55, 67, 77, 84, 85, 92, 43, 67]
[6, 8, 43, 55, 67, 77, 84, 85, 92, 67]
[6, 8, 43, 55, 67, 67, 77, 84, 85, 92]

更容易理解的版本

data_set = [9, 1, 22, 9, 31, -5, 45, 3, 6, 2, 11]
for i in range(len(data_set)):
    position = i
    while i > 0 and data_set[i] < data_set[i - 1]:  # 右边小于左边相邻的值
        tmp = data_set[i]
        data_set[i] = data_set[i - 1]
        data_set[i - 1] = tmp
        i -= 1
    position = i
    while position > 0 and data_set[position] < data_set[position - 1]:  # 右边小于左边相邻的值
        tmp = data_set[position]
        data_set[position] = data_set[position - 1]
        data_set[position - 1] = tmp
        position -= 1

print(data_set)

快速排序

设要排序的数组是A[0]……A[N-1]，首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为一趟快速排序。值得注意的是，快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动　　

注：在待排序的文件中，若存在多个关键字相同的记录，经过排序后这些具有相同关键字的记录之间的相对次序保持不变，该排序方法是稳定的；若具有相同关键字的记录之间的相对次序发生改变，则称这种排序方法是不稳定的。
要注意的是，排序算法的稳定性是针对所有输入实例而言的。即在所有可能的输入实例中，只要有一个实例使得算法不满足稳定性要求，则该排序算法就是不稳定的。 

排序演示

示例

假设用户输入了如下数组：

下标	0	1	2	3	4	5
数据	6	2	7	3	8	9

创建变量i=0（指向第一个数据）, j=5(指向最后一个数据), k=6(赋值为第一个数据的值)。

我们要把所有比k小的数移动到k的左面，所以我们可以开始寻找比6小的数，从j开始，从右往左找，不断递减变量j的值，我们找到第一个下标3的数据比6小，于是把数据3移到下标0的位置，把下标0的数据6移到下标3，完成第一次比较：

下标	0	1	2	3	4	5
数据	3	2	7	6	8	9

i=0 j=3 k=6

接着，开始第二次比较，这次要变成找比k大的了，而且要从前往后找了。递加变量i，发现下标2的数据是第一个比k大的，于是用下标2的数据7和j指向的下标3的数据的6做交换，数据状态变成下表：

下标	0	1	2	3	4	5
数据	3	2	6	7	8	9

i=2 j=3 k=6

称上面两次比较为一个循环。

接着，再递减变量j，不断重复进行上面的循环比较。

在本例中，我们进行一次循环，就发现i和j“碰头”了：他们都指向了下标2。于是，第一遍比较结束。得到结果如下，凡是k(=6)左边的数都比它小，凡是k右边的数都比它大：

下标	0	1	2	3	4	5
数据	3	2	6	7	8	9

如果i和j没有碰头的话，就递加i找大的，还没有，就再递减j找小的，如此反复，不断循环。注意判断和寻找是同时进行的。

然后，对k两边的数据，再分组分别进行上述的过程，直到不能再分组为止。

注意：第一遍快速排序不会直接得到最终结果，只会把比k大和比k小的数分到k的两边。为了得到最后结果，需要再次对下标2两边的数组分别执行此步骤，然后再分解数组，直到数组不能再分解为止（只有一个数据），才能得到正确结果。

def quick_sort(array, left, right):
    '''

    :param array:
    :param left: 列表的第一个索引
    :param right: 列表最后一个元素的索引
    :return:
    '''
    if left >= right:
        return
    low = left
    high = right
    key = array[low]  # 第一个值

    while low < high:  # 只要左右未遇见
        while low < high and array[high] > key:  # 找到列表右边比key大的值 为止
            high -= 1
        # 此时直接 把key(array[low]) 跟 比它大的array[high]进行交换
        array[low] = array[high]
        array[high] = key

        while low < high and array[low] <= key:  # 找到key左边比key大的值，这里为何是<=而不是<呢？你要思考。。。
            low += 1
            # array[low] =
        # 找到了左边比k大的值 ,把array[high](此时应该刚存成了key) 跟这个比key大的array[low]进行调换
        array[high] = array[low]
        array[low] = key

    quick_sort(array, left, low - 1)  # 最后用同样的方式对分出来的左边的小组进行同上的做法
    quick_sort(array, low + 1, right)  # 用同样的方式对分出来的右边的小组进行同上的做法


if __name__ == '__main__':
    array = [96, 14, 10, 9, 6, 99, 16, 5, 1, 3, 2, 4, 1, 13, 26, 18, 2, 45, 34, 23, 1, 7, 3, 22, 19, 2]
    # array = [8,4,1, 14, 6, 2, 3, 9,5, 13, 7,1, 8,10, 12]
    print("before sort:", array)
    quick_sort(array, 0, len(array) - 1)

    print("-------final -------")
    print(array)

 

二叉树

树的特征和定义

　　树是一种重要的非线性数据结构，直观地看，它是数据元素（在树中称为结点）按分支关系组织起来的结构，很象自然界中的树那样。树结构在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构都可用树形象表示。树在计算机领域中也得到广泛应用，如在编译源程序时，可用树表示源程序的语法结构。又如在数据库系统中，树型结构也是信息的重要组织形式之一。一切具有层次关系的问题都可用树来描述。

 

树(Tree)是元素的集合。我们先以比较直观的方式介绍树。下面的数据结构是一个树：

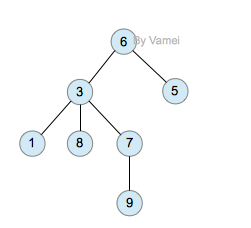
树有多个节点(node)，用以储存元素。某些节点之间存在一定的关系，用连线表示，连线称为边(edge)。边的上端节点称为父节点，下端称为子节点。树像是一个不断分叉的树根。

每个节点可以有多个子节点(children)，而该节点是相应子节点的父节点(parent)。比如说，3,5是6的子节点，6是3,5的父节点；1,8,7是3的子节点, 3是1,8,7的父节点。树有一个没有父节点的节点，称为根节点(root)，如图中的6。没有子节点的节点称为叶节点(leaf)，比如图中的1,8,9,5节点。从图中还可以看到，上面的树总共有4个层次，6位于第一层，9位于第四层。树中节点的最大层次被称为深度。也就是说，该树的深度(depth)为4。

 

如果我们从节点3开始向下看，而忽略其它部分。那么我们看到的是一个以节点3为根节点的树：

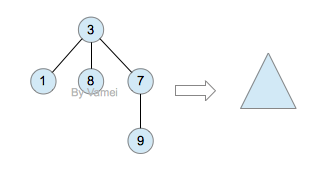
三角形代表一棵树

再进一步，如果我们定义孤立的一个节点也是一棵树的话，原来的树就可以表示为根节点和子树(subtree)的关系:

 

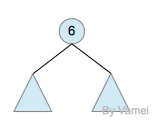
上述观察实际上给了我们一种严格的定义树的方法：

1. 树是元素的集合。

2. 该集合可以为空。这时树中没有元素，我们称树为空树 (empty tree)。

3. 如果该集合不为空，那么该集合有一个根节点，以及0个或者多个子树。根节点与它的子树的根节点用一个边(edge)相连。

上面的第三点是以递归的方式来定义树，也就是在定义树的过程中使用了树自身(子树)。由于树的递归特征，许多树相关的操作也可以方便的使用递归实现。我们将在后面看到。

 

树的实现

树的示意图已经给出了树的一种内存实现方式: 每个节点储存元素和多个指向子节点的指针。然而，子节点数目是不确定的。一个父节点可能有大量的子节点，而另一个父节点可能只有一个子节点，而树的增删节点操作会让子节点的数目发生进一步的变化。这种不确定性就可能带来大量的内存相关操作，并且容易造成内存的浪费。

一种经典的实现方式如下:

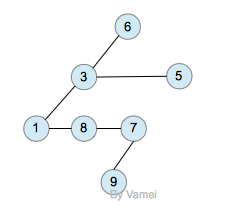
树的内存实现

拥有同一父节点的两个节点互为兄弟节点(sibling)。上图的实现方式中，每个节点包含有一个指针指向第一个子节点，并有另一个指针指向它的下一个兄弟节点。这样，我们就可以用统一的、确定的结构来表示每个节点。

 

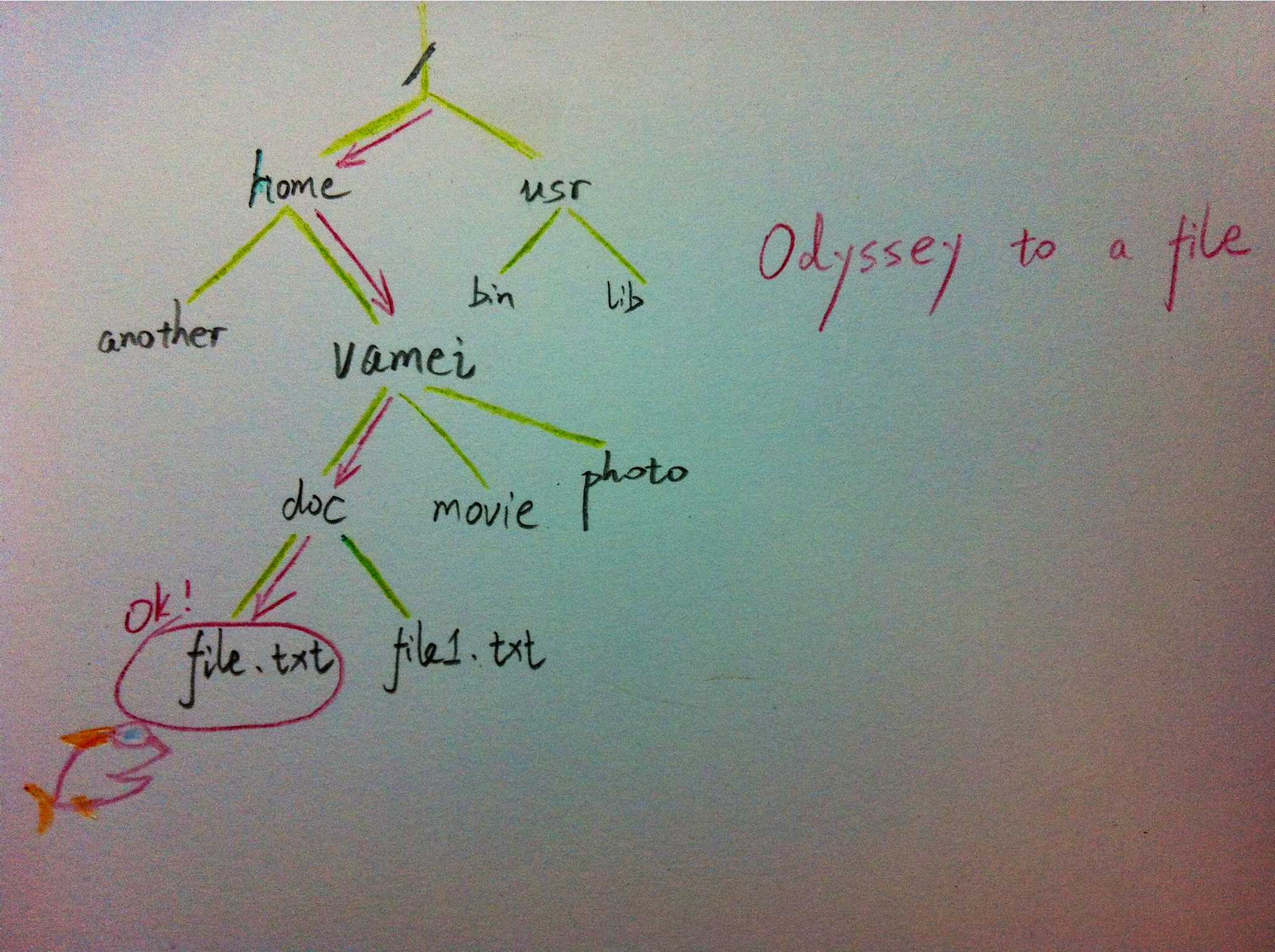
计算机的文件系统是树的结构，比如Linux文件管理背景知识中所介绍的。在UNIX的文件系统中，每个文件(文件夹同样是一种文件)，都可以看做是一个节点。非文件夹的文件被储存在叶节点。文件夹中有指向父节点和子节点的指针(在UNIX中，文件夹还包含一个指向自身的指针，这与我们上面见到的树有所区别)。在git中，也有类似的树状结构，用以表达整个文件系统的版本变化 (参考版本管理三国志)。

 

 

 

 

 

 二叉树：　

二叉树是由n（n≥0）个结点组成的有限集合、每个结点最多有两个子树的有序树。它或者是空集，或者是由一个根和称为左、右子树的两个不相交的二叉树组成。

特点：

（1）二叉树是有序树，即使只有一个子树，也必须区分左、右子树；

（2）二叉树的每个结点的度不能大于2，只能取0、1、2三者之一；

（3）二叉树中所有结点的形态有5种：空结点、无左右子树的结点、只有左子树的结点、只有右子树的结点和具有左右子树的结点。

 

二叉树(binary)是一种特殊的树。二叉树的每个节点最多只能有2个子节点：

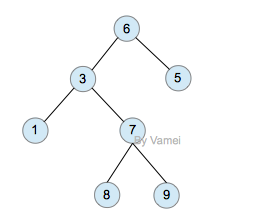
二叉树

由于二叉树的子节点数目确定，所以可以直接采用上图方式在内存中实现。每个节点有一个左子节点(left children)和右子节点(right children)。左子节点是左子树的根节点，右子节点是右子树的根节点。

 

如果我们给二叉树加一个额外的条件，就可以得到一种被称作二叉搜索树(binary search tree)的特殊二叉树。二叉搜索树要求：每个节点都不比它左子树的任意元素小，而且不比它的右子树的任意元素大。

(如果我们假设树中没有重复的元素，那么上述要求可以写成：每个节点比它左子树的任意节点大，而且比它右子树的任意节点小)

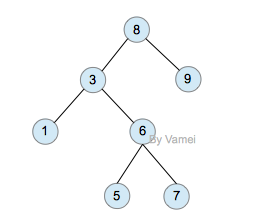
二叉搜索树，注意树中元素的大小

二叉搜索树可以方便的实现搜索算法。在搜索元素x的时候，我们可以将x和根节点比较:

1. 如果x等于根节点，那么找到x，停止搜索 (终止条件)

2. 如果x小于根节点，那么搜索左子树

3. 如果x大于根节点，那么搜索右子树

二叉搜索树所需要进行的操作次数最多与树的深度相等。n个节点的二叉搜索树的深度最多为n，最少为log(n)。

 

二叉树的遍历

遍历即将树的所有结点访问且仅访问一次。按照根节点位置的不同分为前序遍历，中序遍历，后序遍历。

前序遍历：根节点->左子树->右子树

中序遍历：左子树->根节点->右子树

后序遍历：左子树->右子树->根节点

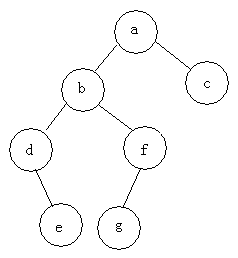
例如：求下面树的三种遍历

 

前序遍历：abdefgc

中序遍历：debgfac

后序遍历：edgfbca

 

 二叉树的类型

(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

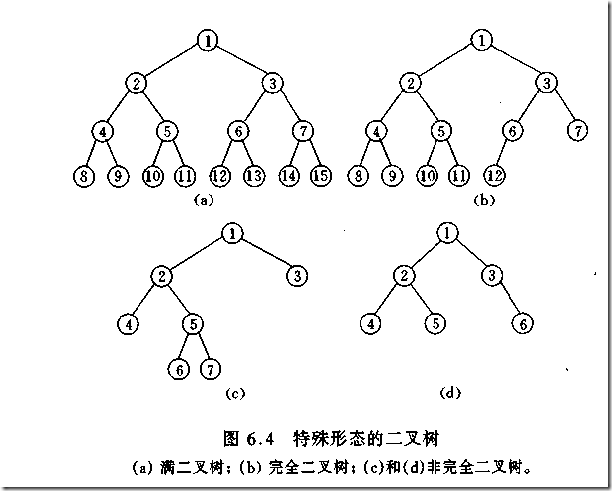
如何判断一棵树是完全二叉树？按照定义，

教材上的说法：一个深度为k，节点个数为 2^k - 1 的二叉树为满二叉树。这个概念很好理解，

就是一棵树，深度为k，并且没有空位。

首先对满二叉树按照广度优先遍历（从左到右）的顺序进行编号。

一颗深度为k二叉树，有n个节点，然后，也对这棵树进行编号，如果所有的编号都和满二叉树对应，那么这棵树是完全二叉树。

 

 

class TreeNode(object):
    def __init__(self,data=0,left=0,right=0):
        self.data = data
        self.left = left
        self.right = right
 
class BTree(object):
    def __init__(self,root=0):
        self.root = root
 
 
    def preOrder(self,treenode):
        if treenode is 0:
            return
        print(treenode.data)
        self.preOrder(treenode.left)
        self.preOrder(treenode.right)
    def inOrder(self,treenode):
        if treenode is 0:
            return
        self.inOrder(treenode.left)
        print(treenode.data)
        self.inOrder(treenode.right)
 
    def postOrder(self,treenode):
        if treenode is 0:
            return
        self.postOrder(treenode.left)
        self.postOrder(treenode.right)
        print(treenode.data)
if __name__ == '__main__':
    n1  = TreeNode(data=1)
    n2 = TreeNode(2,n1,0)
    n3 = TreeNode(3)
    n4 = TreeNode(4)
    n5 = TreeNode(5,n3,n4)
    n6 = TreeNode(6,n2,n5)
    n7 = TreeNode(7,n6,0)
    n8 = TreeNode(8)
    root = TreeNode('root',n7,n8)
 
    bt = BTree(root)
    print("preOrder".center(50,'-'))
    print(bt.preOrder(bt.root))
 
    print("inOrder".center(50,'-'))
    print (bt.inOrder(bt.root))
 
    print("postOrder".center(50,'-'))
    print (bt.postOrder(bt.root))

堆排序

堆排序，顾名思义，就是基于堆。因此先来介绍一下堆的概念。
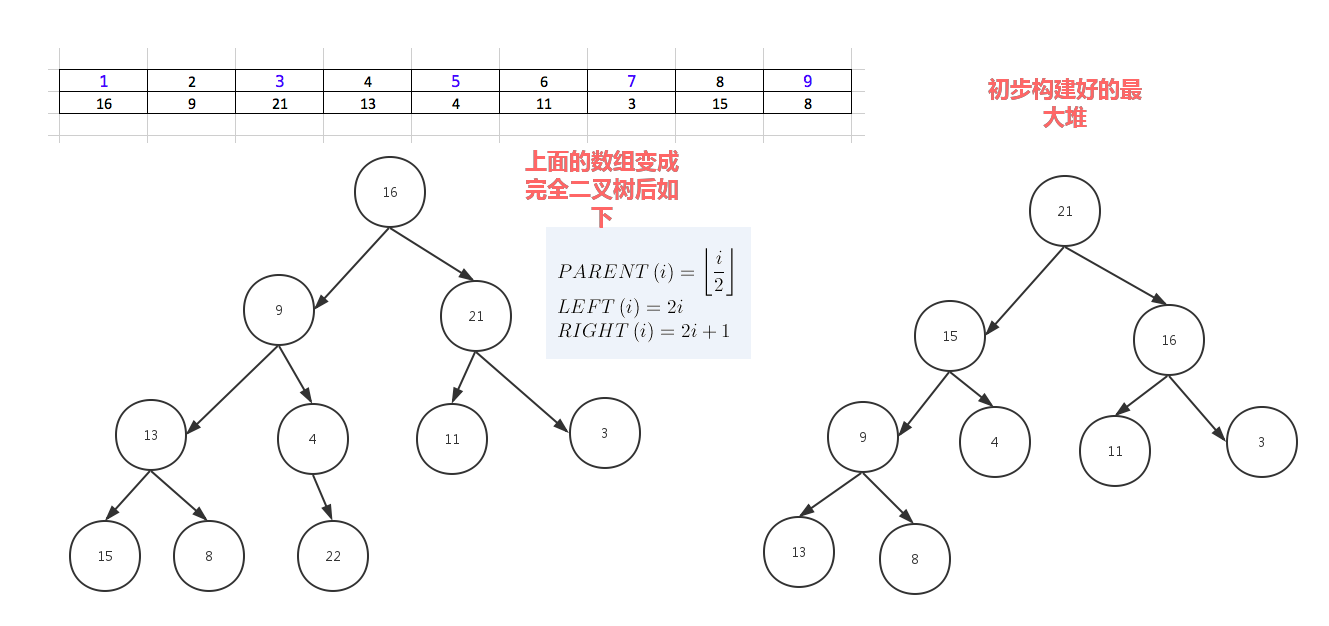
堆分为最大堆和最小堆，其实就是完全二叉树。最大堆要求节点的元素都要大于其孩子，最小堆要求节点元素都小于其左右孩子，两者对左右孩子的大小关系不做任何要求，其实很好理解。有了上面的定义，我们可以得知，处于最大堆的根节点的元素一定是这个堆中的最大值。其实我们的堆排序算法就是抓住了堆的这一特点，每次都取堆顶的元素，将其放在序列最后面，然后将剩余的元素重新调整为最大堆，依次类推，最终得到排序的序列。

 

堆排序就是把堆顶的最大数取出,

将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现

剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束

 

import time, random


def sift_down(arr, node, end):
    root = node
    # print(root,2*root+1,end)
    while True:
        # 从root开始对最大堆调整

        child = 2 * root + 1  # left child
        if child > end:
            # print('break',)
            break
        print("v:", root, arr[root], child, arr[child])
        print(arr)
        # 找出两个child中交大的一个
        if child + 1 <= end and arr[child] < arr[child + 1]:  # 如果左边小于右边
            child += 1  # 设置右边为大

        if arr[root] < arr[child]:
            # 最大堆小于较大的child, 交换顺序
            tmp = arr[root]
            arr[root] = arr[child]
            arr[child] = tmp

            # 正在调整的节点设置为root
            # print("less1:", arr[root],arr[child],root,child)

            root = child  #
            # [3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
            # print("less2:", arr[root],arr[child],root,child)
        else:
            # 无需调整的时候, 退出
            break
    # print(arr)
    print('-------------')


def heap_sort(arr):
    # 从最后一个有子节点的孩子还是调整最大堆
    first = len(arr) // 2 - 1
    for i in range(first, -1, -1):
        sift_down(arr, i, len(arr) - 1)
    # [29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
    print('--------end---', arr)
    # 将最大的放到堆的最后一个, 堆-1, 继续调整排序
    for end in range(len(arr) - 1, 0, -1):
        arr[0], arr[end] = arr[end], arr[0]
        sift_down(arr, 0, end - 1)
        # print(arr)


def main():
    # [7, 95, 73, 65, 60, 77, 28, 62, 43]
    # [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
    # l = [3, 1, 4, 9, 6, 7, 5, 8, 2, 10]
    # l = [16,9,21,13,4,11,3,22,8,7,15,27,0]
    array = [16, 9, 21, 13, 4, 11, 3, 22, 8, 7, 15, 29]
    # array = []
    # for i in range(2,5000):
    #    #print(i)
    #    array.append(random.randrange(1,i))

    print(array)
    start_t = time.time()
    heap_sort(array)
    end_t = time.time()
    print("cost:", end_t - start_t)
    print(array)
    # print(l)
    # heap_sort(l)
    # print(l)


if __name__ == "__main__":
    main()

人类能理解的版本

dataset = [16,9,21,3,13,14,23,6,4,11,3,15,99,8,22]

for i in range(len(dataset)-1,0,-1):
    print("-------",dataset[0:i+1],len(dataset),i)
    #for index in range(int(len(dataset)/2),0,-1):
    for index in range(int((i+1)/2),0,-1):
        print(index)
        p_index = index

        l_child_index = p_index *2 - 1
        r_child_index = p_index *2
        print("l index",l_child_index,'r index',r_child_index)
        p_node = dataset[p_index-1]
        left_child =  dataset[l_child_index]

        if p_node < left_child:  # switch p_node with  left child
            dataset[p_index - 1], dataset[l_child_index] = left_child, p_node
            # redefine p_node after the switch ,need call this val below
            p_node = dataset[p_index - 1]

        if r_child_index < len(dataset[0:i+1]): #avoid right out of list index range
        #if r_child_index < len(dataset[0:i]): #avoid right out of list index range
            #print(left_child)
            right_child =  dataset[r_child_index]
            print(p_index,p_node,left_child,right_child)

            # if p_node <  left_child: #switch p_node with  left child
            #     dataset[p_index - 1] , dataset[l_child_index] = left_child,p_node
            #     # redefine p_node after the switch ,need call this val below
            #     p_node = dataset[p_index - 1]
            #
            if p_node < right_child: #swith p_node with right child
                dataset[p_index - 1] , dataset[r_child_index] = right_child,p_node
                # redefine p_node after the switch ,need call this val below
                p_node = dataset[p_index - 1]

        else:
            print("p node [%s] has no right child" % p_node)


    #最后这个列表的第一值就是最大堆的值，把这个最大值放到列表最后一个， 把神剩余的列表再调整为最大堆

    print("switch i index", i, dataset[0], dataset[i] )
    print("before switch",dataset[0:i+1])
    dataset[0],dataset[i] = dataset[i],dataset[0]
    print(dataset)

希尔排序（shell sort）

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本,该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高

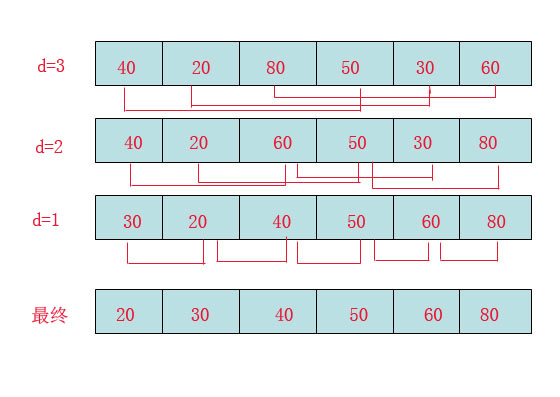
首先要明确一下增量的取法：

      第一次增量的取法为： d=count/2;

      第二次增量的取法为:  d=(count/2)/2;

      最后一直到: d=1;

看上图观测的现象为：

        d=3时：将40跟50比，因50大，不交换。

                   将20跟30比，因30大，不交换。

                   将80跟60比，因60小，交换。

        d=2时：将40跟60比，不交换，拿60跟30比交换，此时交换后的30又比前面的40小，又要将40和30交换，如上图。

                   将20跟50比，不交换，继续将50跟80比，不交换。

        d=1时：这时就是前面讲的插入排序了，不过此时的序列已经差不多有序了，所以给插入排序带来了很大的性能提高。

import time,random

#source = [8, 6, 4, 9, 7, 3, 2, -4, 0, -100, 99]
#source = [92, 77, 8,67, 6, 84, 55, 85, 43, 67]

source = [ random.randrange(10000+i) for i in range(10000)]
#print(source)



step = int(len(source)/2) #分组步长

t_start = time.time()


while step >0:
    print("---step ---", step)
    #对分组数据进行插入排序

    for index in range(0,len(source)):
        if index + step < len(source):
            current_val = source[index] #先记下来每次大循环走到的第几个元素的值
            if current_val > source[index+step]: #switch
                source[index], source[index+step] = source[index+step], source[index]

    step = int(step/2)
else: #把基本排序好的数据再进行一次插入排序就好了
    for index in range(1, len(source)):
        current_val = source[index]  # 先记下来每次大循环走到的第几个元素的值
        position = index

        while position > 0 and source[
                    position - 1] > current_val:  # 当前元素的左边的紧靠的元素比它大,要把左边的元素一个一个的往右移一位,给当前这个值插入到左边挪一个位置出来
            source[position] = source[position - 1]  # 把左边的一个元素往右移一位
            position -= 1  # 只一次左移只能把当前元素一个位置 ,还得继续左移只到此元素放到排序好的列表的适当位置 为止

        source[position] = current_val  # 已经找到了左边排序好的列表里不小于current_val的元素的位置,把current_val放在这里
    print(source)

t_end = time.time() - t_start

print("cost:",t_end)