【2】机器学习之线性回归
一、概述
1、线性回归(Linear Regression)是利用线性方程对一个或多个自变量和因变量之间关系进行建模的一种回归分析。
2、回归的起源
“回归”这个词源于弗朗西斯·高尔顿爵士(英文:Sir Francis Galton,1822年2月16日-1911年1月17日)。
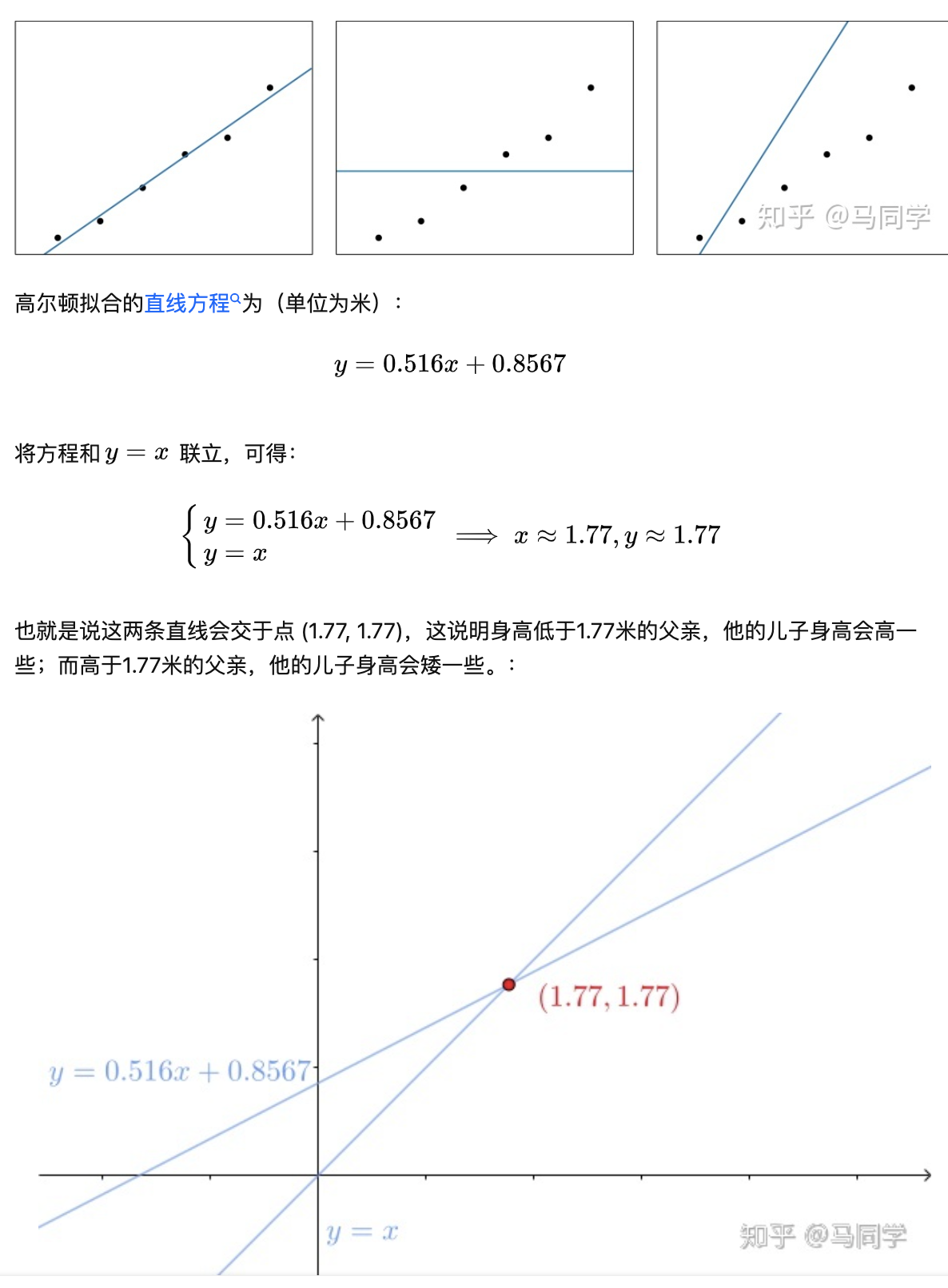
他发现高个子父亲的儿子身高会矮一些,而矮个子父亲的儿子身高会高一些(否则高个子家族会越来越高,而矮个子家族会越来越矮),也就是说人类的身高都会回到平均值附近,他通过抽样一些父子的身高,拟合出来一条直线,其实就表示了回归现象,因此拟合直线的过程被称为 线性回归(Linear Regression)。
以下是拟合过程:
3、回归按照变量个数分为简单回归和多元回归
一元回归:只有一个自变量的情况,也称简单回归
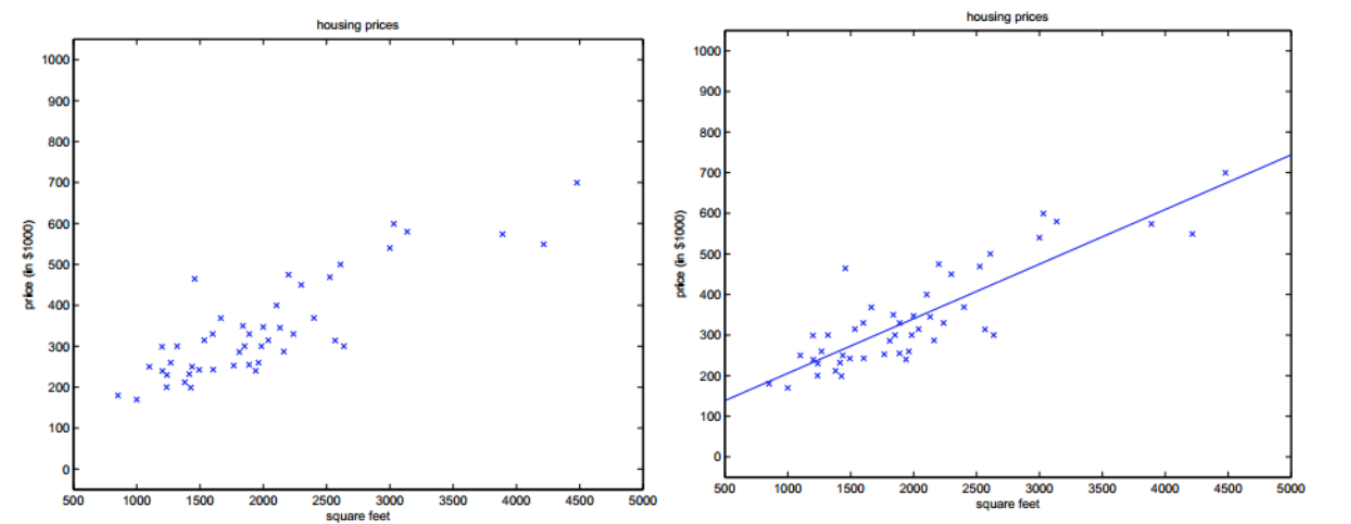
多元回归:大于一个自变量的情况
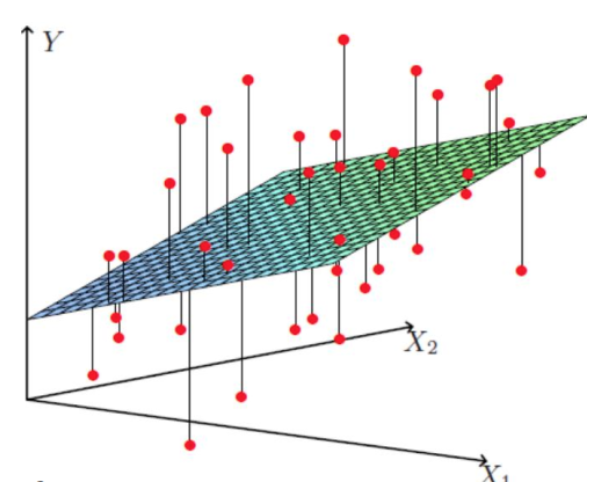
线性回归的优缺点:
优点
1、算法简单,模型容易理解
2、结果可解释,并且易于说明
缺点
1、对于非线性数据或者数据特征间回归难以建模
2、预测精确度较低,变量间相关性影响
二、线性回归的数学表示
2.1 方程组表示形式:
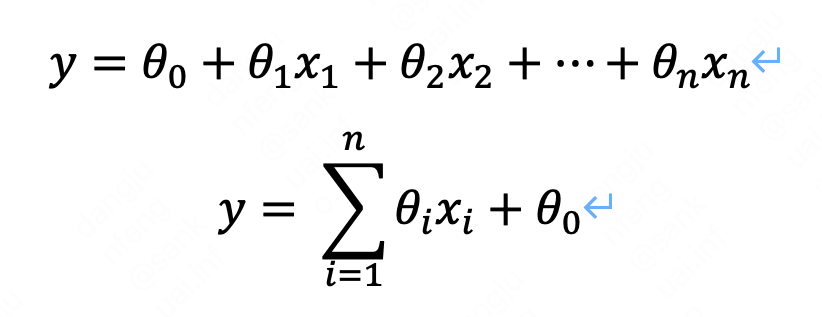
也可以用以下形式表示,其中x1=1
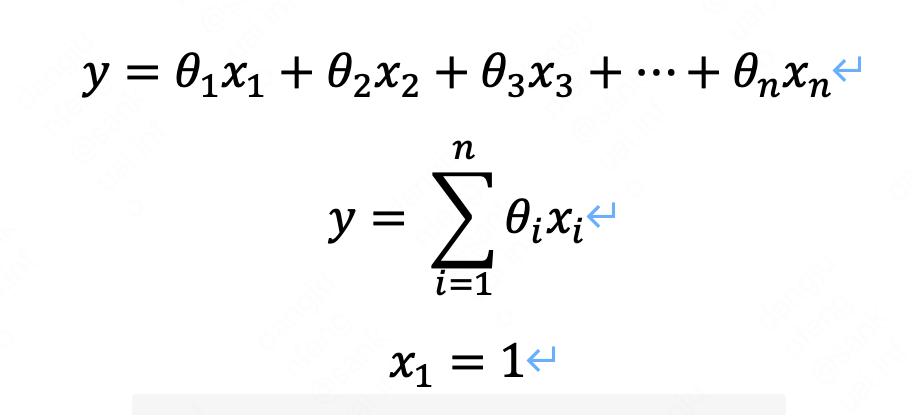
2.2 矩阵表示形式:
三、线性回归求解
回归方程求解其实就是求参数theta使回归方程能更好的拟合并预测数据,这里就要引入一个概念叫损失函数,损失函数定义了回归函数预测值与实际值的误差。
线性回归的损失函数为最小二乘损失函数(MSE):
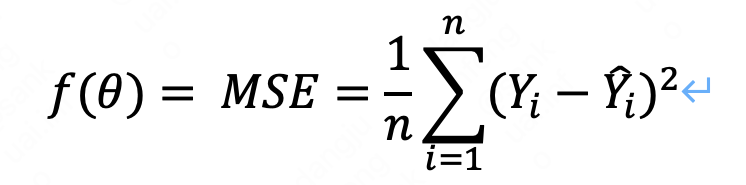
即各个实际值与预测值之差的平方之和。
线性回归函数或者说回归模型的拟合过程其实就是一个最小化损失函数的过程,即求得一个theta使得损失函数最小,从而是拟合效果最优。
如何求最小值
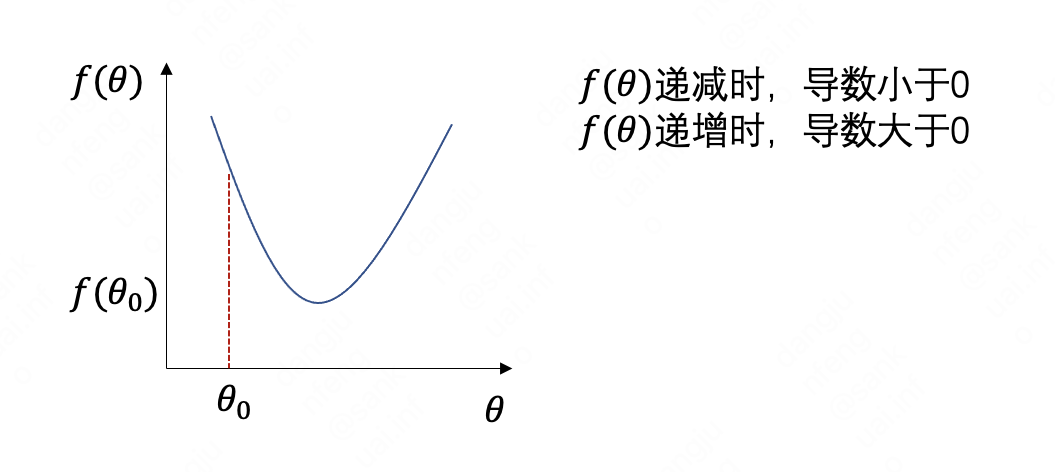
首先理解回归方程的损失函数图像,是一个凸函数,图形类似下图:
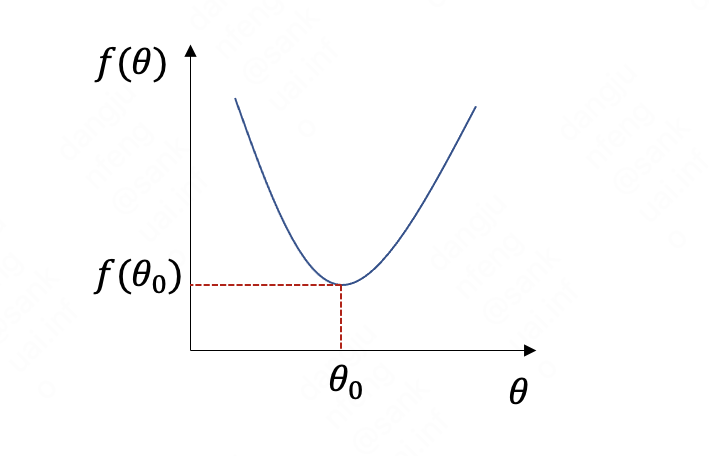
凸函数具有全局最优解,从图形上看,我们可以快速找到最小的theta和对应的损失函数。
我们知道,在数学中,对函数求导, 使得函数的导数为0时,即可获得函数的极值,而损失函数是凸函数,极值即为极小值点。所以,就将其转化为求导取极值问题。
求解方法1:矩阵方程直接求解
推导过程:

从以上推导过程即可转化为求解参数theta,只需要将样本对应数据代入公式即可,具体推导可见链接。
方程求解实现简单,但是它也有一个问题,就是对矩阵求逆的计算时间复杂度为n(特征数量)的2.4次方到3次方,当特征数量变多时,计算时间太长,而且矩阵的秩为0时不可求逆,该方法就无法进行。所以就有了梯度下降法。
求解方法2:梯度下降法
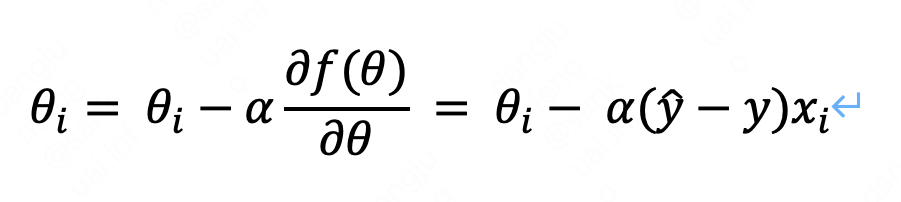
梯度下降法:给定初始theta,通过对损失函数求偏导确定theta的下降梯度方向,然后定义一个学习率alpha,theta每次按沿梯度方向迭代,直到损失函数无限趋近于最小值,当一次迭代中损失函数的变化小于设定的极小值时,便可停止迭代得出theta的近似解。具体推导可见链接
梯度下降的学习率参数需谨慎设置。学习率过小会延长训练时间,大大增加迭代次数,学习率太大又会导致不能收敛,在极小值左右两边摇摆。
四、线性回归系数
1、线性回归系数的含义
系数为正时,说明自变量与因变量正相关,系数为负时,说明自变量与因变量负相关。
系数的大小不能直接说明某个自变量对因变量的影响大小,因为系数跟自变量的量级有关系,量级太大可能拟合系数很小。可以通过对变量标准化,标准化后系数大小可以代表对因变量影响的大小。
2、多重共性问题
多元线性回归会存在多重共性问题,主要表现为增加一个变量对原来变量符号产生影响。多重共性不会影响拟合值和拟合效果,但是变量系数符号会产生异常。
多重共性主要是存在变量之间强线性相关,从而增加变量会导致系数共享,从而产生符号变化。
因此,相关性强的指标需要做处理或删除。判定或检测多重共线性最常用的方法是计算方差膨胀因子(VIF),然后根据VIF的大小判定多重共线性。
比如人口数和交易金额,交易金额会受人口的影响,两个指标可能会存在强相关性,可以对交易金额做人均处理以消除人口影响。
五、模型验证
通常训练模型时,可以将样本分为训练集和测试集。通过训练集训练线性回归模型,再使用测试集验证模型的准确度。准确度可以通过损失函数MES衡量,但是MES是绝对值,跟输出变量的量级有关系,可能结果很大,导致不好衡量模型的好坏,建议使用MAPE验证。
MAPE,平均绝对百分比误差,取值范围[0%,+∞),MAPE越小代表模型效果越好。MAPE 为0%表示完美模型,MAPE 大于 100 %则表示劣质模型,通常在20%以内模型拟合效果较好。
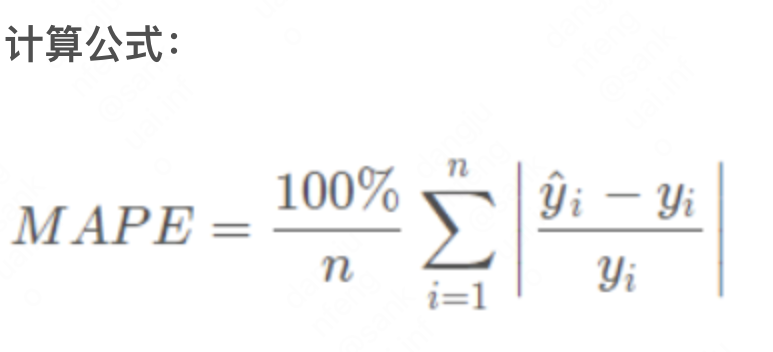
其中,n为验证集记录条数,两个y分别为预测拟合值和实际值
六、python示例
 直接求解
直接求解
 梯度下降
梯度下降

import numpy as np from sklearn import linear_model # y=3x+1,x=1,2,3,4,5,y=4,7,10,13,16 x = np.array([1,2,3,4,5]).reshape(5,1) print('x对应的矩阵:\n',x) y = np.array([4,7,10,13,16]).reshape(5,1) print('y对应的矩阵:\n',y) lr=linear_model.LinearRegression() lr.fit(x, y) coef=lr.coef_ intercept=lr.intercept_ print('系数:\n',coef) print('常量:\n',intercept)


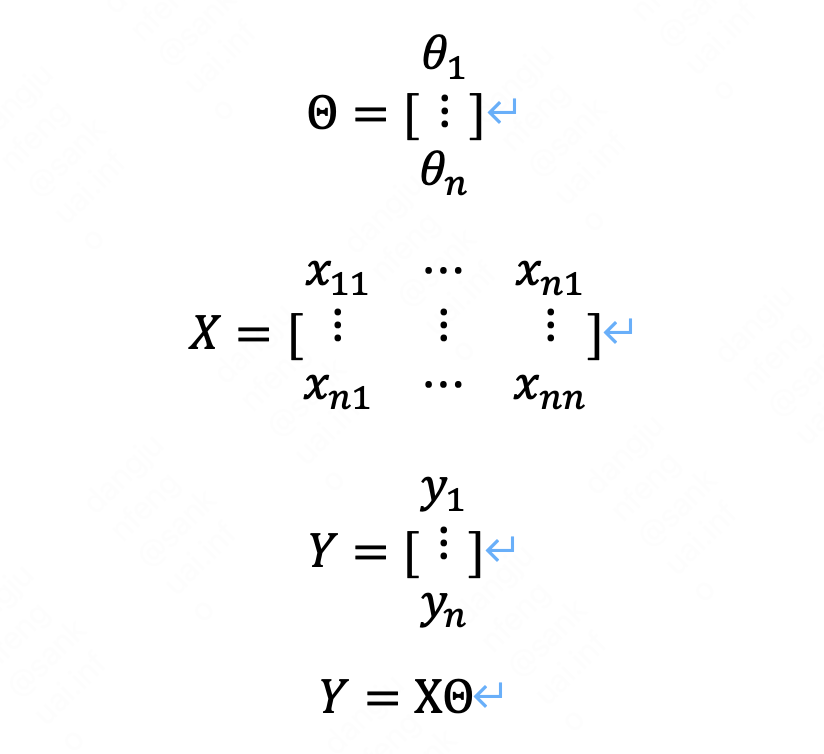


 浙公网安备 33010602011771号
浙公网安备 33010602011771号