Dijkstra算法的C++实现
版权所有,转载请注明出处!
对于该算法的实现思想网上已经有很多,所以这里只是简单介绍原理,重点在于实现代码。
Dijkstra 算法,又叫迪科斯彻算法(Dijkstra),算法解决的是有向图中单个源点到其他顶点的最短路径问题。
举例来说,如果图中的顶点表示城市,而边上的权重表示著城市间开车行经的距离,Dijkstra 算法可以用来找
到两个城市之间的最短路径。
它的实现如下:
Dijkstra 算法的输入包含了一个有权重的有向图 G,以及G中的一个来源顶点 S。我们以 V 表示 G 中所有顶点的集合,
以 E 表示G 中所有边的集合。(u, v) 表示从顶点 u 到 v 有路径相连,而边的权重则由权重函数 w: E → [0, ∞] 定义。
因此,w(u, v) 就是从顶点 u 到顶点 v 的非负花费值(cost),边的花费可以想像成两个顶点之间的距离。
任两点间路径的花费值,就是该路径上所有边的花费值总和。
已知有 V 中有顶点 s 及 t,Dijkstra 算法可以找到 s 到 t 的最低花费路径(例如,最短路径)。这个算法也可以在一个图中,
找到从一个顶点 s 到任何其他顶点的最短路径。
引用算法导论中的伪代码:
DIJKSTRA(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s)
2 S ← Ø
3 Q ← V[G] //V*O(1)
4 while Q ≠ Ø
5 do u ← EXTRACT-MIN(Q) //EXTRACT-MIN,V*O(V),V*O(lgV)
6 S ← S ∪{u}
7 for each vertex v ∈ Adj[u]
8 do RELAX(u, v, w) //松弛技术,E*O(1),E*O(lgV)。
1 INITIALIZE-SINGLE-SOURCE(G, s)
2 S ← Ø
3 Q ← V[G] //V*O(1)
4 while Q ≠ Ø
5 do u ← EXTRACT-MIN(Q) //EXTRACT-MIN,V*O(V),V*O(lgV)
6 S ← S ∪{u}
7 for each vertex v ∈ Adj[u]
8 do RELAX(u, v, w) //松弛技术,E*O(1),E*O(lgV)。
好了,下面给出我自己的实现代码以及运行结果:
//
// main.cpp
// testC++05
//
// Created by fei dou on 12-8-7.
// Copyright (c) 2012年 vrlab. All rights reserved.
//
#include <iostream>
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
int map[][5] = { //定义有向图
{0, 10, INT_MAX, INT_MAX, 5},
{INT_MAX, 0, 1, INT_MAX, 2},
{INT_MAX, INT_MAX, 0, 4, INT_MAX},
{7, INT_MAX, 6, 0, INT_MAX},
{INT_MAX, 3, 9, 2, 0}
};
void Dijkstra(
const int numOfVertex, /*节点数目*/
const int startVertex, /*源节点*/
int (map)[][5], /*有向图邻接矩阵*/
int *distance, /*各个节点到达源节点的距离*/
int *prevVertex /*各个节点的前一个节点*/
)
{
vector<bool> isInS; //是否已经在S集合中
isInS.reserve(0);
isInS.assign(numOfVertex, false); //初始化,所有的节点都不在S集合中
/*初始化distance和prevVertex数组*/
for(int i =0; i < numOfVertex; ++i)
{
distance[ i ] = map[ startVertex ][ i ];
if(map[ startVertex ][ i ] < INT_MAX)
prevVertex[ i ] = startVertex;
else
prevVertex[ i ] = -1; //表示还不知道前一个节点是什么
}
prevVertex[ startVertex ] = -1;
/*开始使用贪心思想循环处理不在S集合中的每一个节点*/
isInS[startVertex] = true; //开始节点放入S集合中
int u = startVertex;
for (int i = 1; i < numOfVertex; i ++) //这里循环从1开始是因为开始节点已经存放在S中了,还有numOfVertex-1个节点要处理
{
/*选择distance最小的一个节点*/
int nextVertex = u;
int tempDistance = INT_MAX;
for(int j = 0; j < numOfVertex; ++j)
{
if((isInS[j] == false) && (distance[j] < tempDistance))//寻找不在S集合中的distance最小的节点
{
nextVertex = j;
tempDistance = distance[j];
}
}
isInS[nextVertex] = true;//放入S集合中
u = nextVertex;//下一次寻找的开始节点
/*更新distance*/
for (int j =0; j < numOfVertex; j ++)
{
if (isInS[j] == false && map[u][j] < INT_MAX)
{
int temp = distance[ u ] + map[ u ][ j ];
if (temp < distance[ j ])
{
distance[ j ] = temp;
prevVertex[ j ] = u;
}
}
}
}
}
int main (int argc, const char * argv[])
{
int distance[5];
int preVertex[5];
for (int i =0 ; i < 5; ++i )
{
Dijkstra(5, i, map, distance, preVertex);
for(int j =0; j < 5; ++j)
{
int index = j;
stack<int > trace;
while (preVertex[index] != -1) {
trace.push(preVertex[index]);
index = preVertex[index];
}
cout << "路径:";
while (!trace.empty()) {
cout<<trace.top()<<" -- ";
trace.pop();
}
cout <<j;
cout <<" 距离是:"<<distance[j]<<endl;
}
}
return 0;
}
运行效果如下图: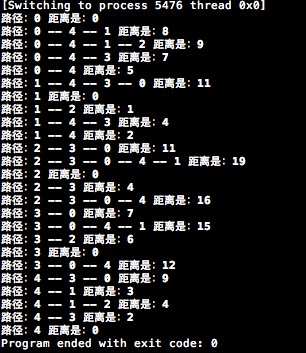



 浙公网安备 33010602011771号
浙公网安备 33010602011771号