9-3做题记录
4003: [JLOI2015]城池攻占
Time Limit: 20 Sec Memory Limit: 128 MBSubmit: 1340 Solved: 505
[Submit][Status][Discuss]
Description
小铭铭最近获得了一副新的桌游,游戏中需要用 m 个骑士攻占 n 个城池。
Input
第 1 行包含两个正整数 n;m,表示城池的数量和骑士的数量。
Output
输出 n + m 行,每行包含一个非负整数。其中前 n 行分别表示在城池 1 到 n 牺牲的骑士
Sample Input
50 20 10 10 30
1 1 2
2 0 5
2 0 -10
1 0 10
20 2
10 3
40 4
20 4
35 5
Sample Output
2
0
0
0
1
1
3
1
1
#include <stdio.h> #include <cstring> #include <vector> #include <cstdlib> #include <algorithm> using namespace std; typedef long long ll; vector<ll> vec[300010]; struct Node { ll val, fa, left, right, times, add, suc; } tree[300010]; ll dist[300010]; ll n, m, sj[300010], success[300010], firstcc[300010], attack[300010], killed[300010], fy[300010], a[300010], v[300010], cases, x, y, root[300010], ans; ll push_down(ll x) { if (tree[x].right) { ll rt = tree[x].right; tree[rt].val *= tree[x].times; tree[rt].val += tree[x].add; tree[rt].times *= tree[x].times; tree[rt].add *= tree[x].times; tree[rt].add += tree[x].add; tree[rt].suc += tree[x].suc; success[rt] += tree[x].suc; } if (tree[x].left) { ll rt = tree[x].left; tree[rt].val *= tree[x].times; tree[rt].val += tree[x].add; tree[rt].times *= tree[x].times; tree[rt].add *= tree[x].times; tree[rt].add += tree[x].add; tree[rt].suc += tree[x].suc; success[rt] += tree[x].suc; } tree[x].times = 1; tree[x].add = 0; tree[x].suc = 0; } ll merge(ll A, ll B) { if (!A || !B) return A + B; if ((tree[A].val > tree[B].val) || (tree[A].val == tree[B].val && A > B)) swap(A, B); ll tmp; push_down(A); push_down(B); tree[A].right = tmp = merge(tree[A].right, B); tree[tmp].fa = A; if (dist[tree[A].right] > dist[tree[A].left]) swap(tree[A].right, tree[A].left); dist[A] = dist[tree[A].right] + 1; return A; } ll get_father(ll A) { return tree[A].fa ? get_father(tree[A].fa) : A; } ll erase(ll A) { tree[tree[A].left].fa = 0; tree[tree[A].right].fa = 0; push_down(A); return merge(tree[A].left, tree[A].right); } void addedge(ll u, ll v) { vec[u].push_back(v); } void dfs(ll x) { //printf("in%lld\n", x); for (ll i = 0; i < vec[x].size(); i++) { dfs(vec[x][i]); root[x] = merge(root[x], root[vec[x][i]]); } /*printf("merged:%lld\n", x); for (ll i = 1; i <= m; i++) { printf("%lld %lld %lld %lld %lld\n", i, tree[i].val, tree[i].times, tree[i].add, tree[i].suc); }*/ while (root[x] && tree[root[x]].val < fy[x]) { root[x] = erase(root[x]); killed[x]++; } if (a[x]) { tree[root[x]].times *= v[x]; tree[root[x]].add *= v[x]; tree[root[x]].val *= v[x]; } else { tree[root[x]].add += v[x]; tree[root[x]].val += v[x]; } tree[root[x]].suc++; success[root[x]]++; } void dfs2(int x) { if (x==0)return ; push_down(x); dfs2(tree[x].left); dfs2(tree[x].right); } int main() { scanf("%lld%lld", &n, &m); for (ll i = 1; i <= n; i++) { scanf("%lld", &fy[i]); } for (ll i = 2; i <= n; i++) { scanf("%lld%lld%lld", &sj[i], &a[i], &v[i]); addedge(sj[i], i); } for (ll i = 1; i <= m; i++) { scanf("%lld%lld", &attack[i], &firstcc[i]); tree[i].val = attack[i]; tree[i].times = 1; tree[i].add = 0; root[firstcc[i]] = merge(root[firstcc[i]], i); } dfs(1); for (ll i = 1; i <= n; i++) { printf("%lld\n", killed[i]); } /*while (root[1]) {root[1] = erase(root[1]); }*/ dfs2(root[1]); for (ll i = 1; i <= m; i++) { printf("%lld\n", success[i]); } //printf("%lld\n", ans); //system("pause"); return 0; }
4195: [Noi2015]程序自动分析
Time Limit: 10 Sec Memory Limit: 512 MBSubmit: 2146 Solved: 1015
[Submit][Status][Discuss]
Description
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
Input
输入文件的第1行包含1个正整数t,表示需要判定的问题个数。注意这些问题之间是相互独立的。
Output
输出文件包括t行。
Sample Input
2
1 2 1
1 2 0
2
1 2 1
2 1 1
Sample Output
YES
HINT
在第一个问题中,约束条件为:x1=x2,x1≠x2。这两个约束条件互相矛盾,因此不可被同时满足。
#include<iostream> #include<cstdio> #include<algorithm> #include<map> #define maxm 1000005 using namespace std; int m,rep[maxm],a[maxm<<1]; map<int,int> Map; struct note{ int x,y,pattern; }query[maxm]; int getrep(int u) { if(rep[u]==u) return u; return rep[u]=getrep(rep[u]); } void init() { for(int i=1;i<=maxm;i++) rep[i]=i; } bool cmp(note a,note b) { return a.pattern>b.pattern; } int main() { int T; scanf("%d",&T); while(T--) { int num=0,id=0; init(); scanf("%d",&m); for(int i=1;i<=m;i++) scanf("%d %d %d",&query[i].x,&query[i].y,&query[i].pattern),a[++num]=query[i].x,a[++num]=query[i].y; sort(a+1,a+1+num); for(int i=1;i<=num;i++) if(a[i]!=a[i-1]||i==1) Map[a[i]]=++id; for(int i=1;i<=m;i++) query[i].x=Map[query[i].x],query[i].y=Map[query[i].y]; sort(query+1,query+1+m,cmp); bool flag=1; int i; for(i=1;i<=m&&query[i].pattern;i++) { int x=query[i].x,y=query[i].y; int fx=getrep(x),fy=getrep(y); if(fx!=fy)rep[fx]=fy; } for(;i<=m&&flag;i++) { int x=query[i].x,y=query[i].y; int fx=getrep(x),fy=getrep(y); if(fx==fy) { flag=0; puts("NO"); } } if(flag)puts("YES"); } return 0; }
统计一下 aaa ⋯ aaan个a × b 的结果里面有多少个数字d,a,b,d均为一位数。
样例解释:
3333333333*3=9999999999,里面有10个9。
多组测试数据。 第一行有一个整数T,表示测试数据的数目。(1≤T≤5000) 接下来有T行,每一行表示一组测试数据,有4个整数a,b,d,n。 (1≤a,b≤9,0≤d≤9,1≤n≤10^9)
对于每一组数据,输出一个整数占一行,表示答案。
2 3 3 9 10 3 3 0 10
10 0
一开始以为只要判断后两位的,摆个竖式就知道要判断后三位~~
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; int a,b,d,n,e,tmp; int main() { int m,num=0; scanf("%d",&m); while(m--) { num++; tmp=0; scanf("%d %d %d %d",&a,&b,&d,&n); if(n<=2) { for(int j=1;j<n;j++) a=a*10+a; a*=b; while(a) { if(a%10==d) tmp++; a/=10; } printf("%d\n",tmp); continue; }else { int tmpc=a*b/10; int tmpd=a*b%10; if(!tmpc) tmp=(tmpd==d)*n;else tmp=(((tmpc+tmpd+(tmpc+tmpd)/10)%10)==d)*(n-2)+(d==tmpd)+(((tmpc+(tmpc+tmpd+(tmpc+tmpd)/10)/10)%10)==d)+((tmpc+tmpd)%10==d); printf("%d\n",tmp); } } return 0; }
题目描述
丽江河边有n 家很有特色的客栈,客栈按照其位置顺序从 1 到n 编号。每家客栈都按照某一种色调进行装饰(总共 k 种,用整数 0 ~ k-1 表示),且每家客栈都设有一家咖啡店,每家咖啡店均有各自的最低消费。
两位游客一起去丽江旅游,他们喜欢相同的色调,又想尝试两个不同的客栈,因此决定分别住在色调相同的两家客栈中。晚上,他们打算选择一家咖啡店喝咖啡,要求咖啡店位于两人住的两家客栈之间(包括他们住的客栈),且咖啡店的最低消费不超过 p 。
他们想知道总共有多少种选择住宿的方案,保证晚上可以找到一家最低消费不超过 p元的咖啡店小聚。
输入输出格式
输入格式:
输入文件hotel.in,共n+1 行。
第一行三个整数n ,k ,p,每两个整数之间用一个空格隔开,分别表示客栈的个数,色调的数目和能接受的最低消费的最高值;
接下来的n 行,第 i+1 行两个整数,之间用一个空格隔开,分别表示 i 号客栈的装饰色调和i 号客栈的咖啡店的最低消费。
输出格式:
输出文件名为hotel.out 。
输出只有一行,一个整数,表示可选的住宿方案的总数。
输入输出样例
5 2 3 0 5 1 3 0 2 1 4 1 5
3
说明
【输入输出样例说明】
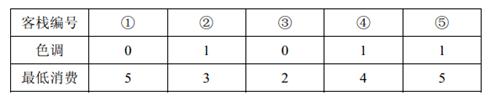
2 人要住同样色调的客栈,所有可选的住宿方案包括:住客栈①③,②④,②⑤,④⑤,但是若选择住4 、5 号客栈的话,4 、5 号客栈之间的咖啡店的最低消费是4 ,而两人能承受的最低消费是3 元,所以不满足要求。因此只有前 3 种方案可选。
【数据范围】
对于30% 的数据,有 n ≤100;
对于50% 的数据,有 n ≤1,000;
对于100%的数据,有 2 ≤n ≤200,000,0<k ≤50,0≤p ≤100 , 0 ≤最低消费≤100。
之前讲过啦,考虑每个客栈做后一个客栈的贡献值,y表示同颜色的前一个客栈,x表示花钱合法的最近前一个客栈,如果y<=x贡献就是所有同颜色的个数,否则就是前一个客栈的贡献值
#include<cstdio> int sum[200008],xia[200008],c[200008]; int n,m,k,ans,x,kind,v; int main() { scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=n;i++){ scanf("%d%d",&kind,&v); if(v<=k)x=i; if(x&&xia[kind]<=x)c[kind]=sum[kind]; sum[kind]++; xia[kind]=i; ans+=c[kind]; } printf("%d",ans); }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号