51nod1580铺管道
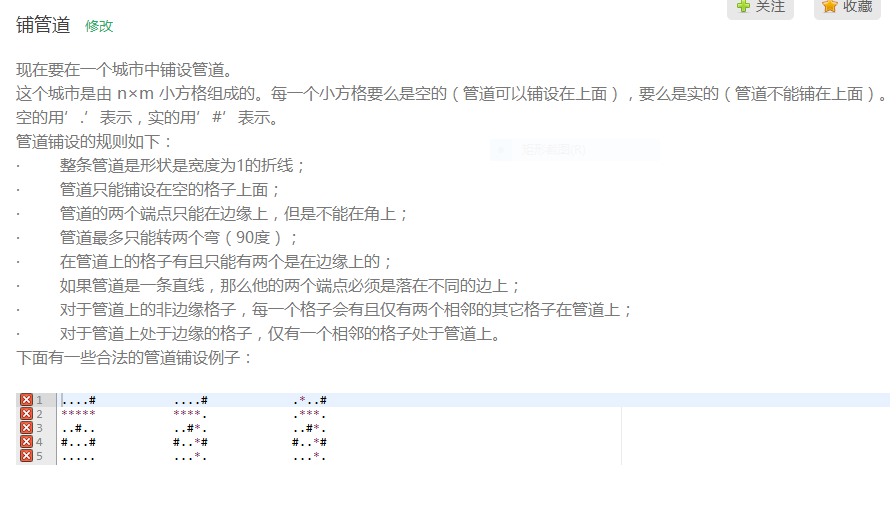

这题的难点在于理解题目和脑洞。
其实我一开始以为这道题是插头DP。原题让我们求的就是各类折线(折两次的,折一次的)以及直直的切线。
代码其实不复杂,画个图理解一下
具体就一下四种情况
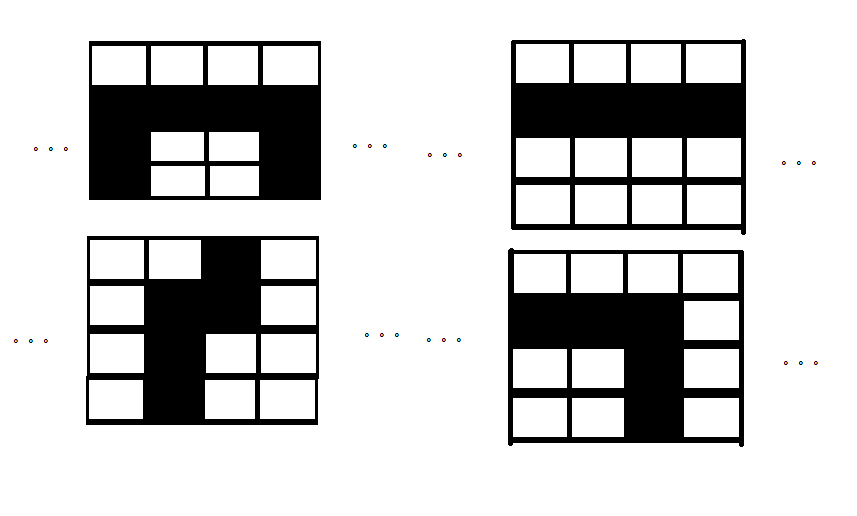
#include <cstdio> #include <iostream> #include <algorithm> #include <cstring> using namespace std; const int MAXN = 2005; int n, m; char S[MAXN]; bool A[MAXN][MAXN], B[MAXN][MAXN]; bool D[MAXN][MAXN], U[MAXN][MAXN]; long long ans = 0; void solve(bool T[][MAXN], int n, int m, int flag) { memset(D, 0, sizeof(D)); memset(U, 0, sizeof(U)); for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { D[i][j] = D[i - 1][j] | T[i][j]; // 是否可以从 T[i - 1][j] 向下到达 T[i][j] 其实是是否可以从T[i][1]向下到达T[i][j] 0表示可以 } } for (int i = n; i; i--) { for (int j = 1; j <= m; j++) { U[i][j] = U[i + 1][j] | T[i][j]; // 是否可以从 T[i + 1][j] 向上到达 T[i][j] 其实是是否可以从T[n][j]向上到达T[i][j] 0表示可以 } } for (int i = 2; i < n; i++) { int tmp = 0; if (!T[i][1] && flag) { tmp = 1; } D[i][1] = U[i][1] = 1; for (int j = 2; j < m; j++) { if (T[i][j]) { tmp = 0; continue; } ans += ((!D[i][j]) + (!U[i][j])) * tmp; // 算 上+[右…右]+下 和 下+[右…右]+上 // 和 上+[右…右]+上 和 下+[右…右]+下 // 以及 从第一列开始 [右…右]+上 和 [右…右]+下 的折线的个数//左上,右上 ans += (!D[i][j] && !U[i][j - 1]) + (!U[i][j] && !D[i][j - 1]); // 算 上+右+上 和 下+右+下 //左上角那张 tmp += (!D[i][j - 1]) + (!U[i][j - 1]); // 算 能到达第 i 行的部分数配合下一次循环使用 } if (!T[i][m] && flag) { ans += tmp + (!D[i][m - 1]) + (!U[i][m - 1]); // 算 从前边任何一列开始 下+[右…右] // 和 上+[右…右] 的情况 以及 左右两端 直达的情况 } } if (flag) { for (int j = 2; j < m; j++) { ans += (!D[n][j]); // 算 上下两端 直达的情况 } } } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i++) { scanf("%s", S + 1); for (int j = 1; j <= m; j++) { A[i][j] = S[j] == '#'; } } solve(A, n, m, 1); for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { B[j][i] = A[i][j]; } } solve(B, m, n, 0); printf("%lld\n", ans);
return 0;
}
代码转自http://blog.csdn.net/f_zyj/article/details/72909671



 浙公网安备 33010602011771号
浙公网安备 33010602011771号