8-3测试总结
。。血崩
题目:
盘子序列
(disk.cpp/c/pas)
【问题描述】
有n个盘子。盘子被生产出来后,被按照某种顺序摞在一起。初始盘堆中如果一个盘子比所有它上面的盘子都大,那么它是安全的,否则它是危险的。称初始盘堆为A,另外有一个开始为空的盘堆B。为了掩盖失误,生产商会对盘子序列做一些“处理”,每次进行以下操作中的一个:(1)将A最上面的盘子放到B最上面;(2)将B最上面的盘子给你。在得到所有n个盘子之后,你需要判断初始盘堆里是否有危险的盘子。
【输入格式】
输入到disk.in
输入文件包含多组数据(不超过10组)
每组数据的第一行为一个整数n
接下来n个整数,第i个整数表示你收到的第i个盘子的大小
【输出格式】
输出到disk.out
对于每组数据,如果存在危险的盘子,输出”J”,否则输出”Y”
【输入输出样例】
|
disk.in |
disk.out |
|
3 2 1 3 3 3 1 2
|
Y J |
【数据范围】
20%的数据保证n<=8
80%的数据保证n<=1,000
100%的数据保证1<=n<=100,000,0<盘子大小<1,000,000,000且互不相等
桌子摆放
(table.cpp/c/pas)
【问题描述】
神犇kblack有很多小弟。
为了庆祝生日,kblack准备在家宴请小弟,他想要邀请尽可能多的小弟来参加他的聚会。他将会和小弟一起坐在一个巨大的长方形桌子上。这个桌子能坐下的人数等于它的周长。
kblack的家可以抽象成一个n*m的矩阵,其中每个位置可能是空地,也可能摆放有其他物品。kblack的桌子的边必须与家的边界平行,并且不能占用任何一个已经占用了的位置。
kblack的粉丝wangyurzee想搞个大新闻,所以他想知道,kblack最多能宴请多少个小弟。但他实在是太弱了,于是向你求助。
【输入格式】
输入文件为table.in
第一行2个正整数n、m,表示kblack家的长宽。
接下来n行,每行m个字符,描述kblack的家。其中”.”表示空地,”X”表示不是空地。
【输出格式】
输出文件为table.out
一行一个整数,表示kblack最多能宴请多少小弟。
【输入输出样例】
|
table1.in |
table1.out |
|
2 2 .. .. |
7 |
|
table2.in |
table |
|
|
9 |
【样例解释】
对于样例1,桌子可以占满整个家,所以其周长为8,减去kblack一人,所以他能宴请7个小弟。
【数据范围】
对于30%的数据,n,m<=1,00;
对于60%的数据,n,m<=4,00;
对于85%的数据,n,m<=1,000;
对于100%的数据,n,m<=1,500;
压轴题
(aknoip.pas/c/cpp)
【题目描述】
现在是NOIP2016 Day2的比赛现场,神犇subconscious0已经秒杀了前两题,再加上他Day1轻松AK,所以现在摆在他面前的就只有这一道压轴题了,只要AC此题,他就能AK NOIP。
根据题面,subconscious0飞快地在大脑中罗列了n个知识点,并且对其中m对知识点建立了联系。每一个联系(u,v,x,y)代表subconscious0从知识点u联想到知识点v需要花费x单位时间,而从知识点v联想到知识点u需要花费y单位时间。
subconscious0发现,他只要从知识点1,经过一系列的联想,再联想回知识点1,便可轻松AC此题。不过在联想中,除了知识点1,必须有其他至少2个知识点被联想到,并且除1外的其他知识点最多都只能被联想到一次。
一旦subconscious0发现不能通过联想法AC此题,那么他便会立即用YJQQQAQ的AC自动机来AC此题。
老年退役选手wangyurzee很想知道,subconscious0至少需要花多少单位时间才能AK NOIP,所以他找到了你,请你帮他计算。如果subconscious0会用AC自动机来AC此题,请输出-1。
【输入格式】
输入文件为aknoip.in
第一行2 个正整数n,m,意义如题。
接下来m 行每行4 个正整数u,v,x,y,描述了一个联系(u,v,x,y)。
数据保证每两个知识点之间最多有一个联系。
【输出格式】
输出文件为aknoip.out
一行一个整数表示答案。
【输入输出样例】
|
aknoip1.in |
aknoip1.out |
|
3 3 1 2 2 3 2 3 1 4 3 1 5 2 |
8 |
|
aknoip2.in |
aknoip2.out |
|
3 2 1 2 1 1 2 3 1 2 |
-1 |
【样例解释】
对于样例1:联想过程为1->2->3->1,所需8个单位时间。
对于样例2:无法用联想法AC此题。
【数据范围】
对于40%的数据:n<=1,000,m<=5,000;
对于100%的数据:1<=n<=40,000,1<=m<=100,000,1<=x,y<=1,000。
【备注】
subconscious0的单位时间远小于1秒,因此subconscious0无论如何都能在1秒内AC此题并AKNOIP。subconscious0太强啦!
题解:(多图预警,流量党慎入)
水题啦,虽然不懂题目什么意思,但是根据样例可以知道就是一个序列能否成为一个有序序列的进栈出栈序列。
模拟+一点优化
首先排个序,然后在原数组中扫描,一个数被拿出的条件就是比这个数小的数全部都已经拿出或已经在栈里面,这个过程暴力操作一下+二分查找。如果我们取出一个数,它在栈里而且不在栈顶我们可以认为这个序列就是不合法的。代码的大图在下面
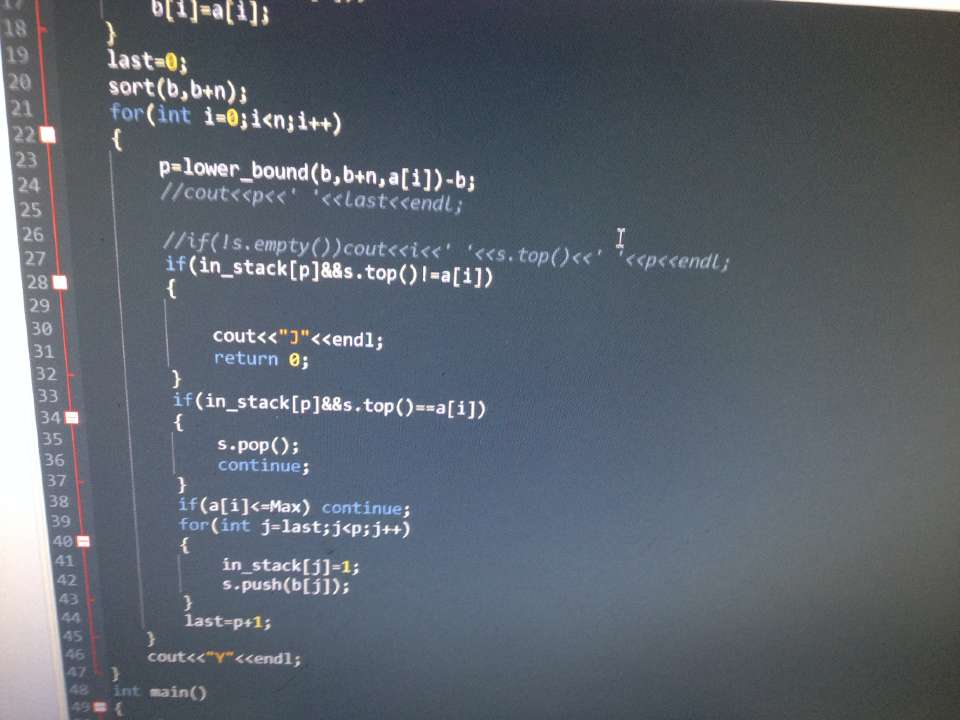

对于每组数据,work()一下,吐血的是——文件名打错了。disk写成了dist。
T2:考试的时候想到了单调栈,但是一直写不对,想的太复杂。这告诉我们总套以前题目的坏处,感觉YH的思路比较简单,先预处理出每个点向上的的连续联通数,枚举每行,
一遍单调栈处理出一个点向左和向右的连续可能数,统计答案,具体见代码~~
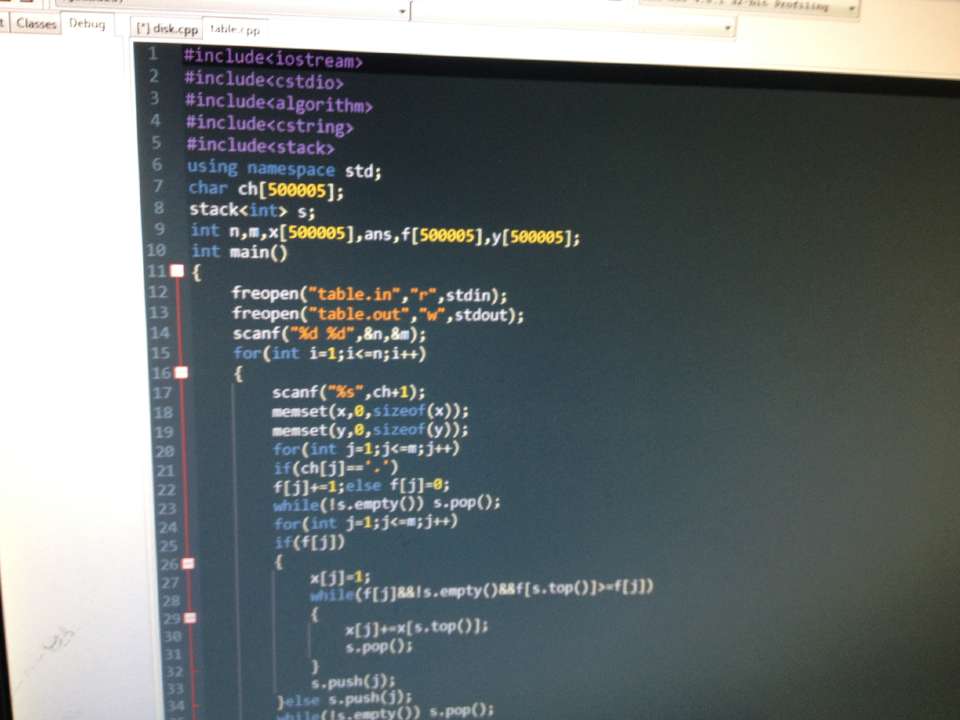

x[i]和y[i]表示向左和向右的扩展数。
调试没删,怒炸90分,脑残了。
T3:一拿到,woc好简单,然而写完dijstra+堆之后懵逼了,有关系吗?
这道题可以想到的方法是把与1相连的边特殊连,然后枚举S,T,跑一遍最短路就可以了。
注意到最短路的性质,其实不用枚举T,枚举S就可以了,60分。
然后就玄学了。
首先为了不超时,我们不能枚举所有的二元组(S,T),60分中也不能对每个点都跑一遍dijstra,这样会超时。所以我们想到了一个高招:将原来的与1相连点集随机分为2个点集,其中一个点集可以从原点直接到达,一个点集只可以能直接到达“原点”,顺便把原点裂成两个点,二元组(S,T)只能同时出现在不同一个点集中,这样时间复杂度大大降低,可以水过,但是期望得分也只有25分(据说不只),怎么办呢?我们可以多做几次,直到快要超时为止,这个功力要求太高,所以我们就做lgn次就好,几乎不会出错。但是这样脸黑怎么办--0~100都有可能。于是乎,我们想到一个靠谱的方法。就是根据点的编号在二进制上的1或0来操作。最后的答案S,T肯定有1位不同。我们在枚举这一位时可以得到正确的答案
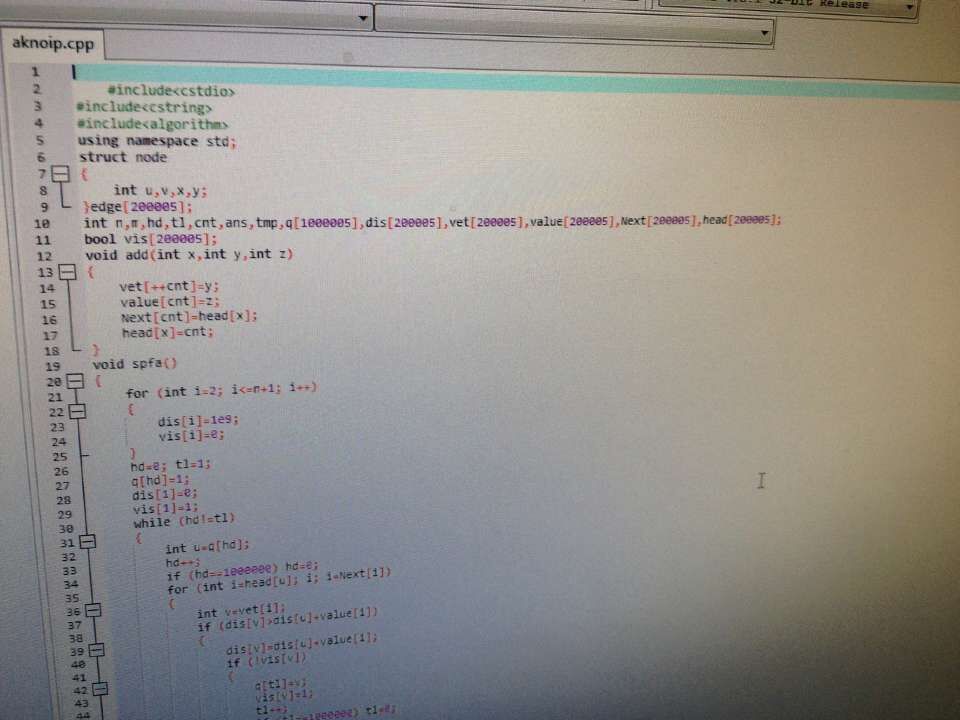
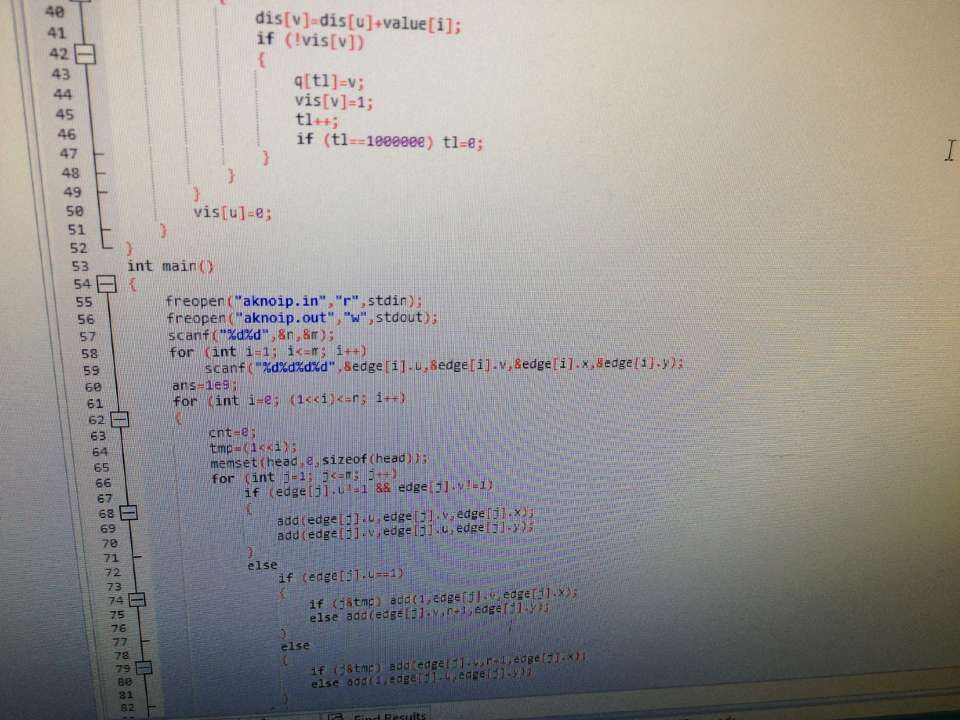
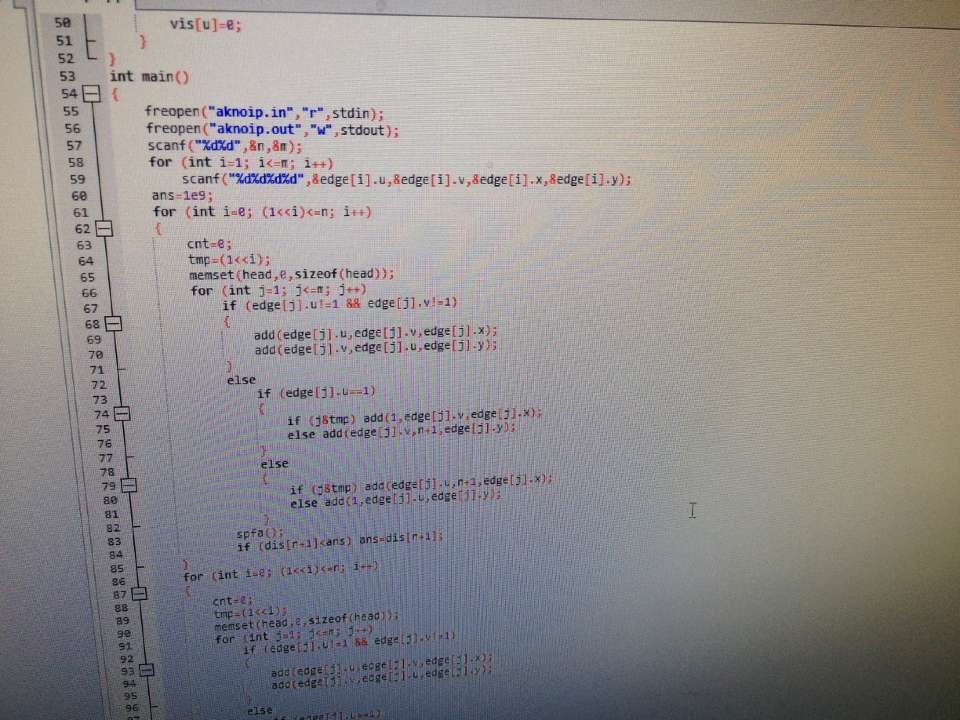
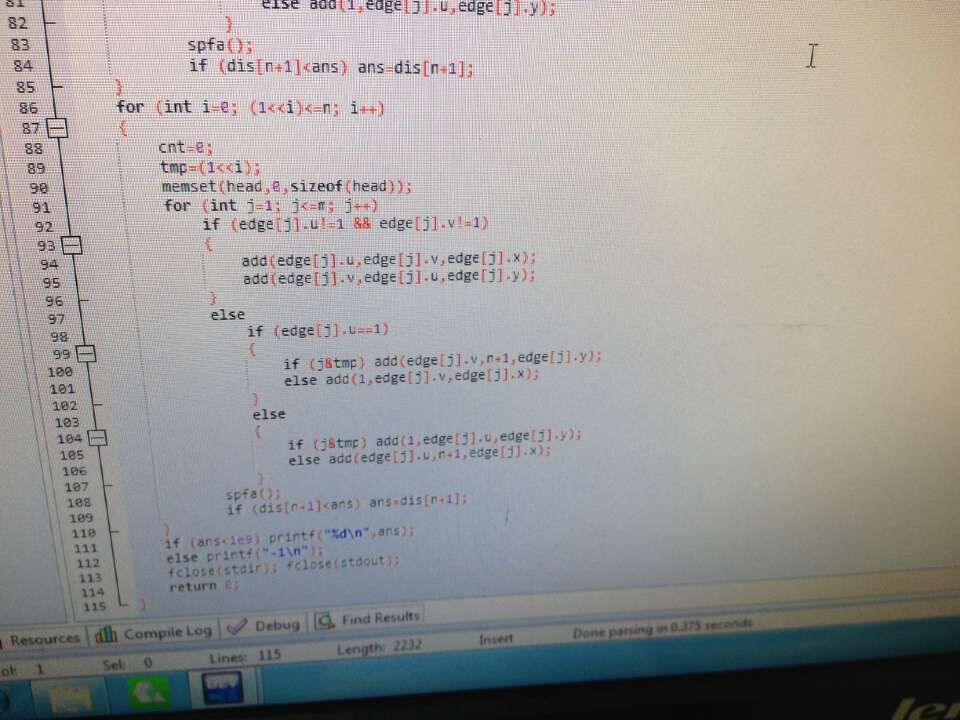



 浙公网安备 33010602011771号
浙公网安备 33010602011771号