7-21测试
问题 A: 挖掘机技术哪家强
时间限制: 1 Sec 内存限制: 128 MB提交: 326 解决: 83
[提交][状态][讨论版]
题目描述
有人问现实中为什么总是男生追求女生,反过来很少。实际上女生也是想主动追求男生的,但是世俗中对于主动追求男生的女生有种歧视,这样就使得女生不大敢主动追求男生。但是面对喜欢的男生,难道就不出手么?女生只能步步为营,挖坑来引诱男生往里跳。这时候问题就来了,挖掘机技术到底哪家强?
被热血沸腾的广告洗脑了若干天后,Matt终于下定决心,毅然登上了开往泉城的列车,决心寻找生活的希望。
来到布鲁谢特学院后,Matt逐渐地了解了各种型号的挖掘机。在这里我们可以认为有大挖掘机和小挖掘机两种。
今天Matt的任务很简单:首先他要用大挖掘机挖出恰好N单位体积的砂土。由于小挖掘机比较笨拙,它每次挖的砂土体积是固定的。也就是说,设每次挖x单位体积砂土,那么N需要被x整除。在挖出若干堆体积为x的砂土后,Matt需要计算x的“难挖指数”。体积x的“难挖指数”定义如下:对于某个不超过x的体积y,如果x与y的最大公约数为1,那我们认为体积y是“难挖的”,x的“难挖指数”就要加上y。
由于Matt之后还需要用小挖掘机处理被大挖掘机挖出的砂土,他希望知道所有可能的x的难挖指数的和,这样他好估算今天要干多久,不然作为布鲁谢特的高才生,他出门要被笑话的。
输入
第一行一个整数T,表示数据组数。
接下来T行每行一个整数表示N。
输出
对于每个数据输出一行一个整数表示难挖指数的和。
样例输入
3 2 3 4
样例输出
2 4 6
提示
题目意思:定义两个函数f,g,并求出g(n)的值: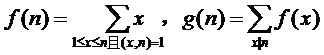 。
。
这道题有一个小定理。小于自然数x的所有与x互质的自然数的和为φ(x)*x/2。因为如果a与x互质,x-a必定与x互质。两两配对即可。
所以原题就变为了求所有是n约束的x的x*φ(x)/2之和。
考场时用质因数分解+爆搜实现了一下,因为数据不是特别大水过了。
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> using namespace std; int n,m,num[10005],prime[10005],s[10005]; long long tot,tmp,ans; void calc() { tot=tmp=1; for(int i=1;i<=m;i++) { tot*=s[i]; } if(tot==1) { ans+=1; return; } tmp=tot; for(int i=1;i<=m;i++) if(s[i]!=1) tmp=tmp*(prime[i]-1)/prime[i]; ans+=tmp*tot/2; } void dfs(int x) { if(x>m) { calc(); return; } s[x]=1;dfs(x+1); for(int i=1;i<=num[x];i++) { s[x]*=prime[x]; dfs(x+1); } s[x]=1; } int main() { int T; scanf("%d",&T); while(T--) { m=ans=0; scanf("%d",&n); for(int i=2;i<=sqrt(n);i++) if(n%i==0) { prime[++m]=i; num[m]=0; while(n%i==0) { num[m]++; n/=i; } if(n==1) break; } if(n!=1) prime[++m]=n,num[m]=1; dfs(1); printf("%lld\n",ans); } }
孤独一生
时间限制: 1 Sec 内存限制: 128 MB提交: 238 解决: 27
[提交][状态][讨论版]
题目描述
下课了,Polo来到球场,但他到了之后才发现…..被放了飞机……
无事可做的他决心找点乐子,比方说……跳台阶……
球场边有N个台阶拍成一行,第i个台阶的高度是Hi(0<Hi<=10^9),第0个台阶,也就是地面的高度为0。Polo打算把这N个台阶分成两个集合Sa,Sb(可以为空),对于一个台阶集合S={P1,P2,...P|S|},其中P1<P2<...<P|S|,他需要花费
sigma{|S| i=1} {Hpi-Hpi-1}
的体力值来完成。
现在他希望两次跳跃所需的总体力值最小,你能帮帮他吗?
输入
第一行一个数N。
第二行N个整数Hi。
输出
一行一个整数,表示最小的总体力值。
样例输入
3 1 3 1
样例输出
4
提示
这道题一开始想到爆搜,但貌似只有10分。后来想到用f[i][j]表示一个集合以i结尾另一个集合以j结尾的最小值。转移:if(i!=j+1) f[i][j]=f[i-1][j]+|h[i]-h[i-1]|;else f[i][j]=min(f[j][k]+h[i]-h[j]);
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; int f[5005][5005],a[5005],n; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); f[0][0]=0; for(int i=1;i<=n;i++) { f[i][0]=f[i-1][0]+abs(a[i]-a[i-1]); for(int j=1;j<i;j++) if(i!=j+1) f[i][j]=f[i-1][j]+abs(a[i]-a[i-1]);else { f[i][j]=0x7FFFFFF; for(int k=0;k<j;k++) f[i][j]=min(f[i][j],f[j][k]+abs(a[i]-a[k])); } } int ans=0x7FFFFFF; for(int l=0;l<n;l++) ans=min(ans,f[n][l]); cout<<ans<<endl; }
然后我们试图去优化它。我们发现当且仅当i=j+1时,f[i][j]的值不能递推。所以我们只要枚举一下每个f[i][i-1]的请况,假设在f[i][i-1]后所有的数都分配到第一个集合里——答案肯定从某个f[i][i-1]中转来。我们令g[i]=f[i][i-1],有方程g[i]=min(g[j]+sum[i-1]-sum[j]+abs(h[i]-h[j-1]));
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #define ll long long using namespace std; ll g[50005],sum[50005],ans=0,a[50005]; int main() { ll n; scanf("%lld",&n); for(ll i=1;i<=n;i++) scanf("%lld",&a[i]),sum[i]+=sum[i-1]+abs(a[i]-a[i-1]); g[1]=a[1];ans=g[1]+sum[n]-sum[1]; for(ll i=2;i<=n;i++) { g[i]=0x7FFFFFFF; for(ll j=1;j<i;j++) { g[i]=min(g[i],g[j]+sum[i-1]-sum[j]+abs(a[i]-a[j-1])); } ans=min(ans,g[i]+sum[n]-sum[i]); } cout<<ans<<endl; }
剩下的我们用数状数组优化一下就可以啦
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<map> #define ll long long using namespace std; map<ll,ll> Map; #define lowbit(x) x&(-x) #define maxn 500005 ll v[maxn],num=1,g[maxn],n,tree_1[maxn],tree_2[maxn]; struct note{ ll a,sum; }point[maxn]; void update_1(ll x,ll val) { for(ll p=x;p<=maxn;tree_1[p]=min(tree_1[p],val),p+=lowbit(p)); } void update_2(ll x,ll val) { for(ll p=x;p<=maxn;tree_2[p]=min(tree_2[p],val),p+=lowbit(p)); } ll query_1(ll x) { ll sum=1000000; for(ll p=x;p;sum=min(sum,tree_1[p]),p-=lowbit(p)); return sum; } ll query_2(ll x) { ll sum=0x7FFFFFFF; for(ll p=x;p;sum=min(sum,tree_2[p]),p-=lowbit(p)); return sum; } int main() { scanf("%lld",&n); memset(tree_1,63,sizeof(tree_1)); memset(tree_2,63,sizeof(tree_2)); for(ll i=1;i<=n;i++) { scanf("%lld",&point[i].a); v[i]=point[i].a; point[i].sum+=point[i-1].sum+abs(point[i].a-point[i-1].a); } sort(v+1,v+1+n); for(ll i=1;i<=n;i++) { if(v[i]!=v[i-1]) { Map[v[i]]=++num; } } ll ans=0x7FFFFFFF; g[1]=point[1].a;ans=point[n].sum; update_1(1,0);update_2(num,0); for(ll i=2;i<=n;i++) { ll s1=query_1(Map[point[i].a]); ll s2=query_2(num-Map[point[i].a]+1); s1+=point[i].a; s2-=point[i].a; g[i]=min(s1,s2)+point[i-1].sum; update_1(Map[point[i-1].a],g[i]-point[i].sum-point[i-1].a); update_2(num-Map[point[i-1].a]+1,g[i]-point[i].sum+point[i-1].a); ans=min(ans,point[n].sum-point[i].sum+g[i]); } cout<<ans<<endl; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号