Value Noise——值噪音
1.简介
Value Noise是最简单的噪声算法，器主要思路是定义若干顶点且每个顶点含有一个随机值，这些顶点会根据自己的随机值对周围坐标产生影响，越靠近顶点则越容易受该顶点影响。当需求某个坐标的输出值是，需要将改坐标附近的各个顶点所造成的影响值进行叠加，从而得到一个总之并输出。
2.原理
2.1首先定义一个晶格结构，每个晶格的顶点有一个伪随机值（Value）。对于二维的Value噪声来说，晶格结构就是一个平面网络（通常是正方形），三维的就是一个立方体。
2.2输入一个点（二维就是二维坐标，三维就是三维坐标，n维就是n维坐标），找到和他相邻的那些劲歌顶点（二维4个，三维下8个），得到这些顶点的伪随机值。
2.3使用缓和曲线来计算这些伪随机值的权重和。原始的噪声使用缓和曲线是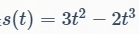
，2002年改进为
。改进后二阶导上仍满足连续，即曲线更平滑。
3.理解
设想一张纹理，uv范围0~1
但是我们讲算法的时候，0~1的范围太小了，最总看起来效果不好，因此我们将uv缩放一下。
现在将网格中的每个焦点都计算出一个随机值，用于后续的噪音计算。
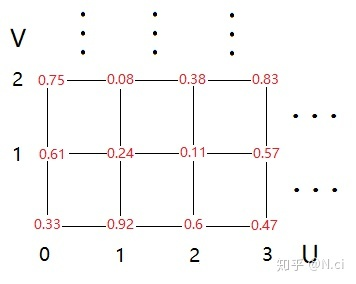
然后如果我们要取出u2.3，v1.6位置的点p的值
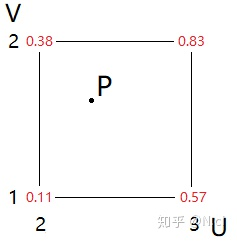
我们根据p值的坐标，对当前晶格的u 2~3求一个差值A，再对v1~2求一个差值B,最后在AB上求一个差值P，如下：
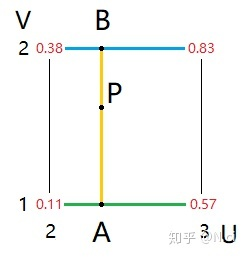
如果求取插值呢？
最明显简单的差值方法，线性插值：
最终得到p的值时0.4082，转换为灰度（0.4082R+0.4082G+0.4082B）。使用这个算法网格上的任何一个位置都可以转换成灰度。
使用线性插值做到了个点间的平滑生成效果如下：
点之间虽然平滑了，但是晶格间的过渡比较生硬。
因为我们使用的是线性插值，
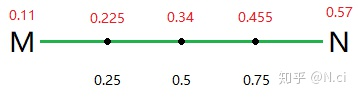
从 M 到 N，插值的方式均匀递增。我们假设后面还有一个节点 Q，并且 Q 的灰度值是 0.02：
将这些值形成连续的图像如下：
从这个图中我们可以明显的看到晶格的交界处过渡生硬。
所以柏林噪声之父提出了缓和曲线计算插值。
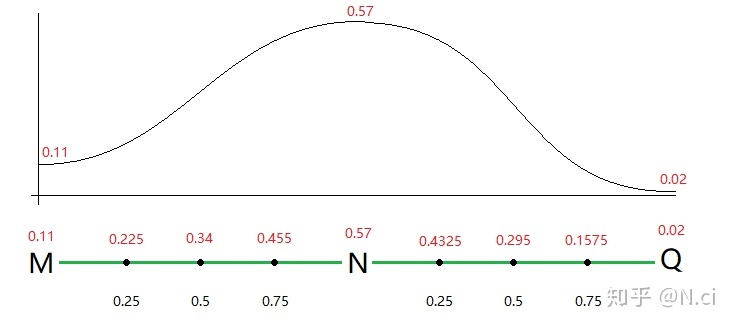
应用到刚刚的m-n-q模型中，效果就平滑很多。
最后结果如下：
