CRF 条件随机场
条件随机场
作者:elfin 参考资料来源:《统计学习方法》第二版
1、概率图模型
概率图定义: 由图表示的概率分布,这个概率分布假设为 \(P\left(Y \right)\) ,\(Y\)是一组随机变量。
由无向图 \(G=\left( V,E \right)\) 表示概率分布 \(P\left(Y \right)\) ,即在图 \(G\) 中,结点 \(v \in V\) 表示一个随机变量 \(Y_{v}\) , \(Y \in \left( Y_{v} \right)_{v \in V}\) ;边 \(e\in E\) 表示随机变量之间的概率依赖关系。
1.1 成对马尔可夫性
定义: 设 \(u\) 和 \(v\) 是无向图 \(G\) 中任意两个没有边连接的结点,结点 \(u\) 和 \(v\) 分别对应随机变量 \(Y_{u}\) 和 \(Y_{v}\) 。其他所有结点为 \(O\) ,对应的随机变量组是 \(Y_{O}\) 。成对马尔可夫性是指 \(Y_{u}\) 和 \(Y_{v}\) 在 \(Y_{O}\) 下条件独立:
1.2 局部马尔可夫性
定义: 设 \(v \in V\) 是无向图 \(G\) 中任意一个结点, \(W\) 是与 \(v\) 有边连接的所有结点, \(O\) 是 \(W\) 和 \(v\) 以外的所有其他结点。 \(v\) 表示的随机变量是 \(Y_{v}\) , \(W\) 表示的随机变量组是 \(Y_{W}\) , \(O\) 表示的随机变量组是 \(Y_{O}\) 。局部马尔可夫性是指在 \(Y_{W}\) 下 \(Y_{O}\) 和 \(Y_{v}\) 条件独立:
若 \(P\left ( Y_{O} | Y_{W} \right ) > 0\) ,等价地有:
局部马尔可夫性的图示:
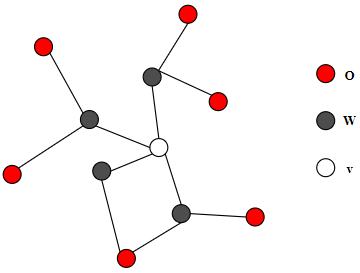
即灰色的点确定后,白色与红色结点条件独立。
1.3 全局马尔可夫性
定义: 设结点集合 \(A,B\) 是在无向图 \(G\) 中被结点集合 \(C\) 分开的任意结点集合。则全局马尔可夫性是指在 \(Y_{C}\) 下 \(Y_{A}\) 和 \(Y_{B}\) 条件独立:
全局马尔可夫性图示:
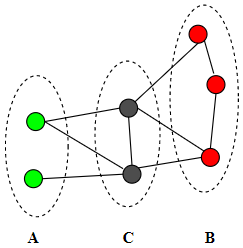
注意在图中,三种马尔可夫性是等价的!
1.4 概率无向图模型
定义: 设有联合概率分布 \(P\left( Y \right)\) ,由无向图 \(G=\left( V,E \right)\) 表示,如果 \(P\left( Y \right)\) 满足成对、局部、全局马尔可夫性,则称此联合概率分布为概率无向图模型,或称马尔可夫随机场。
1.5 马尔可夫随机场的因子分解
团与最大团定义: 无向图 \(G\) 中任何两个结点均有边连接的结点子集称之为团(clique)。若 \(C\) 是无向图 \(G\) 的一个团,并且不能再加一个 \(G\) 的任何结点成为一个更大的团,则称此 \(C\) 为最大团(maximal clique)。
马尔可夫随机场的因子分解: 将概率无向图模型的联合概率分布表示为其最大团的随机变量组的函数的乘积形式。
Hammersley-Clifford 定理: (莫斯利-克利福德定理) 概率无向图模型的联合概率分布 \(P\left( Y \right)\) 可以表示为如下形式:
其中, \(C\) 是无向图的最大团,\(Y_{C}\) 是 \(C\) 的结点对应的随机变量组, \(\Psi_{C} \left ( Y_{C} \right )\) 是 \(C\) 上定义的严格正函数,乘积是在无向图中所有的最大团上进行的。
函数 \(\Psi_{C} \left ( Y_{C} \right )\) 是势函数,通常定义为:
1.6 Hammersley-Clifford 定理证明(莫斯利-克利福德定理证明)
首先满足公式\((5)\)的分布为吉布斯分布,所以我们需要证明的就是 吉布斯分布 \(\rightleftharpoons\) MRF(马尔可夫随机场)
1.6.1 吉布斯分布 \(\rightarrow\) MRF
这部分我们要证明:满足吉布斯分布,则\(P\left ( Y_{v} | Y_{W} \right ) = P\left ( Y_{v} | Y_{W},Y_{O} \right )\),即满足[局部马尔可夫性](#1.2 局部马尔可夫性)。
证明:
接着,我们将是否包含\(Y_{C}\)将最大团结合\(C_{G}\)分为两组:
- \(H = \left \{ C \mid C \in C_{G}, Y_{v} \in C \right \}\),包含\(Y_{v}\)的最大团集合;
- \(R = \left \{ C \mid C \in C_{G}, Y_{v} \notin C \right \}\),不包含\(Y_{v}\)的最大团集合;
根据\(H,R\)我们把公式\((7)\)拆分为:
因为\(O\)是不包含\(W,v\)的,所以\(O\)中节点不可能出现在\(H\)中,即\(H\)中的团包含节点\(v\),若属于\(O\)中的节点\(v_{o}\)在\(H\)中,那么根据最大团的定义,\(v,v_{o}\)是可以直接相连的,说明\(v_{o} \in W\),这与\(O\)的定义矛盾;
公式\((8)\)分子分母都有\(\sum_{O} \prod_{C\in R} \Psi_{C} \left ( Y_{C} \right )\),我们能约掉这一项吗?当然是可以了,\(R,O\)都不包含节点\(v\),所以关于\(Y_{v}\)求和,这一项是一个常量。所以进一步化简有:
所以:\(P\left(Y_{v} \mid Y_{W} \right)=P\left(Y_{v} \mid Y_{V \setminus v}\right)\) ,满足局部马尔可夫性. 得证\(\blacksquare\)
1.6.2 MRF \(\rightarrow\) 吉布斯分布
我们要将MRF的分布函数使用吉布斯分布函数进行表示,首先我们根据其形式构造势函数:
定义: 对于\(\forall \, U\subset V\),\(Y_{U}\)对应的势函数定义为:
关于定义有以下几点说明:
- 等式右边的乘积是在集合\(U\)的每一个子集上进行;
- \(Y_{Z}=y_{Z},Y_{V \setminus Z} = 0\)是表示属于\(Z\)集合的顶点与集合\(U\)中的取值保持一致,其余默认取零;
- 这里的势函数\(F\)是满足非负定义的!
最后我们只需要证明:
-
\(\prod_{U\subset V} F_{U}\left ( Y_{U} \right )=P\left ( Y \right )\)
这个条件得到证明,我们就有\(P\left ( Y \right )=\prod_{U\subset V} F_{U}\left ( Y_{U} \right )\),即马尔可夫随机场的分布可以由所有子集的势函数乘积得到!
-
\(\prod_{U\subset V \setminus C_{G}} F_{U}\left ( Y_{U} \right )=1\)
所有的最大团一定可以在\(U \subset V\)条件下取到!我们只需要证明不是最大团的子集即\(\prod_{U\subset V \setminus C_{G}} F_{U}\left ( Y_{U} \right )=1\)可!
1.6.2.1 先证明\(\prod_{U\subset V} F_{U}\left ( Y_{U} \right )=P\left ( Y \right )\)
首先,根据公式\((10)\),我们知道对不同的\(U\)我们可能会存在相同的子集\(Z\),即如图所示:
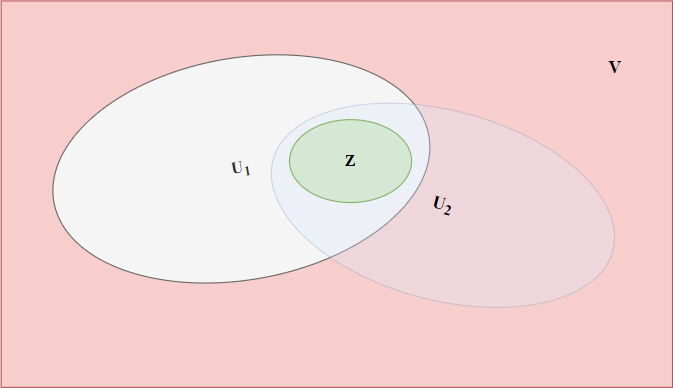
现在我们考虑那些\(U \subset V\)跟\(\forall Z \subset V\)的关系:
对于\(\forall Z \subset V\),我们记\(P_{Z}=P\left ( Y_{Z}=y_{Z},Y_{V \setminus Z} = 0 \right )\)。所以在\(\prod_{U\subset V} F_{U}\left ( Y_{U} \right )\)中,\(P_{Z}\)会出现多少次?
下面我们对所有子集和子集\(Z\)的对比情况进行分类说明:
-
当\(U\)不包含\(Z\)时,那么\(F_{U}\left ( Y_{U} \right )\)中不会出现\(P_{Z}\),因为\(Z\)不是\(U\)的子集!
\(Num\left ( P_{Z} \right )=0\)
-
当\(U=Z\)时,我们知道因为此时\(Z\)是固定的,所以\(U\)是唯一的,则\(P_{Z}\)出现1次;
\(Num\left ( P_{Z} \right )=1\)
-
当\(U \in \left \{ \left \{ Z,Y_{i} \right \} \mid Y_{i} \in V\setminus Z \right \}\),即\(U\)比\(Z\)多一个元素,这样一共有\(\left | V \right | - \left | Z \right |\)个\(U_{i}\),则:
\(Num\left ( P_{Z} \right )=\left | V \right | - \left | Z \right |=\textrm{C}_{\left | V \right | - \left | Z \right |}^{1}\)
此时,实际是我们可以将\(1\)表示 为:\(\textrm{C}_{\left | V \right | - \left | Z \right |}^{0}\)。
-
当\(U \in \left \{ \left \{ Z,Y_{i},Y_{j} \right \} \mid Y_{i},Y_{j} \in V\setminus Z ,i\neq j \right \}\),即\(U\)比\(Z\)多两个元素,这样\(P_{Z}\)就出现\(\left ( \left | V \right | - \left | Z \right | \right )\left ( \left | V \right | - \left | Z \right | -1 \right ) / 2\)次,则:
\(Num\left ( P_{Z} \right )=\textrm{C}_{\left | V \right | - \left | Z \right |}^{2}\)
-
\(\cdots\)
-
当\(U=V\)时,即\(U\)比\(Z\)多\(\left | U \right |-\left | Z \right |=\left | v \right |-\left | Z \right |\)个元素 ,这样\(P_{Z}\)就出现1次,即:
\(Num\left ( P_{Z} \right )=1=\textrm{C}_{\left | V \right | - \left | Z \right |}^{\left | U \right |-\left | Z \right |}\)
-
这个规律就很明显了,\(Num\left ( P_{Z} \right )=\textrm{C}_{\left | V \right | - \left | Z \right |}^{\left | U \right |-\left | Z \right |}\),\(P_{Z}\)的出现次数在不同的\(\left | U \right |-\left | Z \right |\)上满足一个组合数分布!
所以我们要证明的等式左边有:
关于\(\sum_{i} (-1)^{\textrm{C}_{\left | V \right | - \left | Z \right |}^{i}},\,i\in \left \{ 0,1,\cdots ,\left | V \right | - \left | Z \right | \right \}\),其值恰好是\(\left(1+ (-1) \right)^{\left | V \right | - \left | Z \right |}\)展开形式,即:
即我们一直在算\(0^{i}\),那不是全部等于0?注意\(0^{0}=1\)。我们考虑一下什么时候取到\(0^{0}\),不就是\(\left | V \right | - \left | Z \right |=0\)嘛!所以我们得出结论:
当且仅当\(Z=V\)时,\(P_{Z}\)的系数不为0,所以有:
所以,\(\prod_{U\subset V} F_{U}\left ( Y_{U} \right )=P\left ( Y \right )\)得证\(\blacksquare\)
1.6.2.2 证明\(\prod_{U\subset V \setminus C_{G}} F_{U}\left ( Y_{U} \right )=1\)
我们先证明所有不是团的子集\(F_{U}\left ( Y_{U} \right )=1\)。
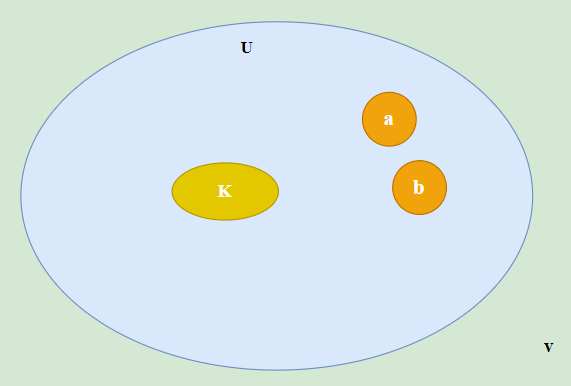
根据团的定义,若\(U\)不是团,那么\(U\)中至少存在两个节点\(a,b\)使得节点间没有边直接连接。对于\(U\)的所有子集我们可以使用
\(\forall \, Z \subset U\setminus (a,b)\),\(\left \{ Z,\{Z,a\}, \{Z,b\},\{Z,a,b\} \mid \forall Z\subset U\setminus \{a,b\} \right \}\)标识了所有的子集。所以势函数\(F_{U}\left ( Y_{U} \right )\)有:
注意上式的分母来源于指数部分的\(-1\),即本来应该是四部分相乘,但是比\(Z\)多一个元素则指数部分也多乘了\(-1\),写到分母上就能在指数部分保持一致!
式(14)这一项可以继续分解,根据贝叶斯定理(条件概率):
根据马尔可夫性,在\(Y_{Z},Y_{V\setminus Z}\)已知的情况下,就只有节点\(Y_{a},Y_{b}\)没有确定,而他们是独立的,所以\(Y_{b}=0\)可以进行替换,即:
结合\((14)\)、\((16)\),我们有:
所以不是团的势函数\(F_{U}\left ( Y_{U} \right )=1\)。得证\(\blacksquare\)
以下片段未完成证明
经过上面的分析,我们已经可以证明无向图满足局部马尔科夫性,则联合概率分布可以分解为所有团的联合概率分布的乘积形式。而在最大团因子分解定理中,我们只使用了最大团,所有的团是包含了最大团的,同时也包含了普通团,接下来我们需要证明非最大团的团其势函数乘积为1!
证明:最大团\(C\)的所有非空真子集势函数乘积为\(C\)的势函数!
首先,关于最大团\(C\)所有非空真子集势函数的乘积\(G(C)\)为:
这个形式看起来并没有什么特点,下面我们引入一个中间量\(K\),它是最大团的一个子集,其本身也是一个团,我们记:
当\(G(C)\)中的\(U\)选择不同时,关于\(P_{K}\)项的指数是怎样的?
-
当\(U\)不包含\(K\)时,\(P_{K}\)不会出现;
-
当\(K \subset U\)时:
- 若\(\left | U \right | - \left | K \right |=0\),\(P_{K}\)指数为1;
- 若\(\left | U \right | - \left | K \right |=1\),\(P_{K}\)指数为-1;
- \(\cdots\)
- 若\(\left | U \right | - \left | K \right |=\left | C \right | - \left | K \right |\),\(P_{K}\)指数为\((-1)^{\left | C \right | - \left | K \right |}\);
这里,我们还是看不出有什么规律,但是注意团\(K\)是标量,相应地\(\left | C \right | - \left | K \right |\)也是一个标量,指数和这个量是密切相关的!下面我们从另一个角度改写。
-
当\(K \subset U\)时:
- 当\(\left | U \right | - \left | K \right |=0\),相当于从补集\(C\setminus K\)中选出\(0\)个元素与\(K\)合并组成新的子集,我们一共有\(\textbf{C}_{\left | U \right | - \left | K \right |}^{0}\)中不同取法;则,对所有$$\left | U \right | - \left | K \right |=0$$的\(P_{K}\)指数和为:\(\textbf{C}_{\left | C \right | - \left | K \right |}^{\left | U \right | - \left | K \right |} \,\cdot\, (-1)^{\left | U \right | - \left | K \right |}\)。(这里有上面的铺垫我就直接写出递推的形式)
- 当\(\left | U \right | - \left | K \right |=1\),\(P_{K}\)的指数和为:\(\textbf{C}_{\left | U \right | - \left | K \right |}^{1} \,\cdot\, (-1)^{1}\)。
- \(\cdots\)
- 当\(\left | U \right | - \left | K \right |=\left | C \right | - \left | K \right |\),\(P_{K}\)指数和为\(\textbf{C}_{\left | C \right | - \left | K \right |}^{\left | U \right | - \left | K \right |} \,\cdot\, (-1)^{\left | U \right | - \left | K \right |}\)。(这一项实际上是没有的)
-
所以关于\(P_{K}\)项的指数和为:
\[\sum_{i=0}^{\left | C \right | - \left | K \right |}\textbf{C}_{\left | C \right | - \left | K \right |}^{i} \,\cdot\, (-1)^{i} \]所以指数和为0?,为什么不是0?.
因为上面\(K\)需要是\(U\)的真子集时,\(P_{K}\)才存在,上面为了保持形式一致性,并推出\((1-1)^{\left | C \right | - \left | K \right |}\)的组合形式,所以添加了一项,这里我们要在最终求和上减去一个1.
所以最后有:
未证明片段完
2、条件随机场的定义与形成
2.1 条件随机场的定义
条件随机场定义: 设 \(X\) 和 \(Y\) 是随机变量,若随机变量 \(Y\) 构成一个由无向图 \(G=\left( V,E \right)\) 表示的马尔可夫随机场,即:
对任意结点 \(v\) 成立,则称条件概率分布 \(P \left( Y|X \right)\) 为条件随机场。式中 \(w \sim v\) 表示在图 \(G=\left( V,E \right)\) 中与结点 \(v\) 有边连接的所有结点 \(w\) 。
线性链条件随机场定义: 设\(X=\left( X_{1},X_{2},\cdots,X_{n} \right)\),\(Y=\left( Y_{1},Y_{2},\cdots,Y_{n} \right)\)均为线性链表示的随机变量序列,若在给定随机变量序列\(X\)的条件下,随机变量序列\(Y\)的条件概率分布 \(P \left( Y|X \right)\) 构成条件随机场,即满足马尔可夫性:
则称 \(P \left( Y|X \right)\) 为条件随机场。
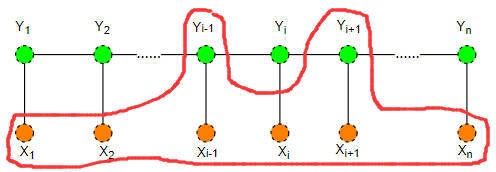
即:图中红色圈内的数据确定后,\(Y_{i}\)的概率分布就唯一确定了!
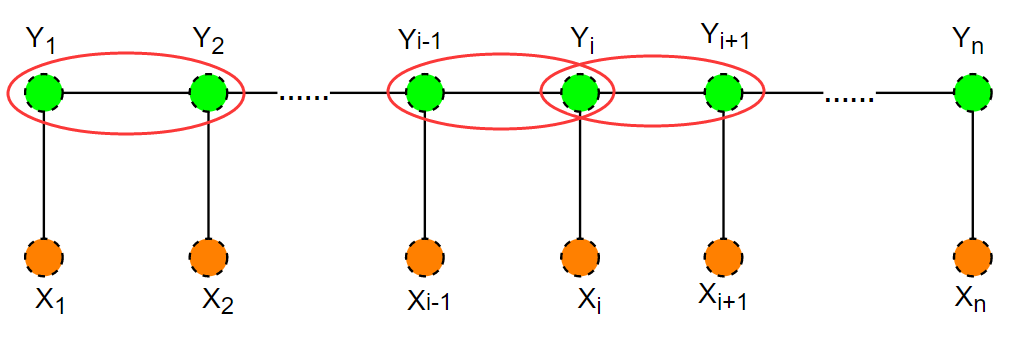
线性链的条件随机场: 对于\(n\)个节点的线性链条件随机场,一共有\(n-1\)个最大团!根据最大团的定义我们有:线性链的相邻两个节点组成最大团。
2.2 条件随机场的参数化形式
线性链条件随机场的参数化形式定义: 设 \(P \left( Y|X \right)\) 为线性链条件随机场,则在随机变量\(X\)取值为\(x\)的条件下,随机变量\(Y\)取值为\(y\)的条件概率具有如下形式:
其中,\(t_{k},\ s_{l}\) 是依赖于当前位置的特征函数,取值为1或0。条件随机场由特征函数\(t_{k},\ s_{l}\) 及其对应的权值\(\lambda_{k},\ \mu_{l}\)确定。
公式\((9)\)是怎么来的?
公式是根据最大团因子分解定理进行构建的,注意不是严格推导而出!
由Hammersley-Clifford 定理有:
\[P\left(y \mid x\right) = \frac{1}{Z\left(x\right)} \prod_{i=2}^{n} e^{-E\left(Y_{C}\right)} =\frac{1}{Z\left(x\right)} \prod_{i=2}^{n} e^{-E\left(y_{i-1},y_{i}, x \right)} \]其中\(n\)是线性链的节点数,所以有\(n-1\)个最大团;\(Y_{C}\)是根最大团\(C\)相关的自变量集。
关键就在于从\((10)\)怎么“推导”出\((9)\)!
能量函数\(E\)是一个黑盒,我们不知道它是什么样的,这个情形和深度学习非常类似。在深度学习模型中,我们也不知道输入与输出之间的关系,但是我们在建模过程中使用了CNN、RNN等组件搭建了一个模型框架,训练过程只是学习权值参数。而在这里我要考虑的是:什么样的函数可以很nice的对能量函数结构性建模,基于数据再进行参数学习得到最终的模型!
在能量函数\(E\left(y_{i-1},y_{i}, x \right)\)中,我们主要涉及到三个部分:节点\(y_{i-1}\),\(y_{i}\),\(edge_{y_{i-1},y_{i}}\)。关于\(x\)输入,它不会随着\(i\)进行变化,这里可以看作一个标量,这也是条件随机场的条件一词的含义,即在条件\(x\)确定的前提下。基于这三部分我们将能量函数拆分为独立的三部分:
\[E\left(y_{i-1},y_{i}, x \right) = f_{1}\left(y_{i-1},x\right) + f_{2}\left(y_{i},x\right) + f_{3}\left(y_{i-1},y_{i},x\right) \]关于子能量\(f_{1}\left(y_{i-1},x\right)\)在\(E\left(y_{i-2},y_{i-1}, x \right)\)也会出现,所以我们进一步简化为:
\[E\left(y_{i-1},y_{i}, x \right) = f_{1}\left(y_{i},x\right) + f_{2}\left(y_{i-1},y_{i},x\right) \]公式\((12)\)就能与公式\((9)\)对应起来了,即:
\[f_{1}\left(y_{i},x\right)=\mu_{l}s_{l} \left( y_{i},x \right)\\ f_{2}\left(y_{i-1},y_{i},x\right) = \lambda_{k}t_{k} \left( y_{i-1}, y_{i}, x \right) \]如上所述:\(t_{k},\ s_{l}\) 是依赖于当前位置的特征函数,也可以理解为示性函数,即满足条件取值为1、反之取值为0。前面已经说了:\(f_{i}\)是子能量,而\(t_{k},s_{l}\)分别是最大团\(C_{i}\)的特征能量(示性能量),\(\lambda_{k},\ \mu_{l}\)即标识了对应条件的能量值!\(k,l\)分别标识了两种子能量的条件数量。
2.3 条件随机场的简化形式
在公式(9)中,我们注意到同一特征在各个 位置都有定义,所以可以对同一特征在各个位置求和,将局部特征函数转换为全局特征函数,这样就可以 将条件随机场写成权值向量与特征向量的内积形式。
设有\(K_{1}\)个转移特征、\(K_{2}\)个状态特征,且\(K=K_{1}+K_{2}\):
对 转移与状态特征在各个位置\(i\)求和,记作:
用\(w_{k}\)表示特征\(f_{k}\left ( y,x \right )\)的权值,得到:
则条件随机场可以表示为:
注意这里的点乘是内积。
2.4 条件随机场的矩阵形式
对观测序列\(x\)的每一个位置\(i=1,2,\cdots,n+1\),由于\(y_{i-1}\)和\(y_{i}\)在\(m\)个标记中取值,可以定义一个\(m\)阶矩阵随机变量(m维的向量):
其中:
则条件随机场可以表示为:
其中:
完!


