LGPMA ------ 基于局部、全局金字塔mask对齐的表格结构识别模型解析
LGPMA:Complicated Table Structure Recognition with Local and Global Pyramid Mask Alignment
基于局部和全局金字塔掩码对齐的复杂表格结构识别
论文:https://arxiv.org/pdf/2105.06224.pdf
Repo:https://github.com/hikopensource/DAVAR-Lab-OCR
这是海康威视开源的一个算法,总的来说算法是比较优秀的!上面的项目也可以持续关注。
摘要
由于表格结构的多样性和复杂的单元生成关系,表格结构识别是一项具有挑战性的任务。以前的方法从不同粒度(行/列、文本区域)的元素开始处理问题,这些元素不知何故落入有损启发式规则或忽略空单元划分等问题中。基于表格结构特征,我们发现获得文本区域的对齐边界框可以有效地保持不同单元格的整个相关范围。然而,由于视觉模糊性,对齐的边界框很难准确预测。在本文中,我们的目标是通过充分利用文本区域在局部特征中的视觉信息和全局特征中的细胞关系来获得更可靠的对齐边界框。具体来说,我们提出了局部和全局金字塔掩模对齐的框架,该框架在局部和全局特征映射中都采用了软金字塔掩模学习机制。它允许边界框的预测边界突破原始方案的限制。然后集成金字塔掩码重新评分模块,以折衷局部和全局信息并细化预测边界。最后,我们提出了一个健壮的表结构恢复管道来获得最终的表结构,有效地解决了空单元的定位和划分问题。实验结果表明,该方法在多个公共基准上取得了有竞争力的甚至是最新的性能。
一、介绍
表是许多真实文档(如财务报表、科学文献、采购清单等)中丰富的信息数据格式之一。除了文本内容之外,表结构对于人们进行关键信息提取至关重要。因此,表格结构识别[10,21,34,30,5,4,39]成为当前文档理解系统中的重要技术之一。
从全局角度来看,早期的表结构识别过程通常依赖于网格边界的检测[19,18]。但是,这些方法不能处理没有网格边界的表,例如三行表。尽管最近的工作[30,22,32,31]试图预测行/列区域,甚至是不可见的网格线[33],但它们仅限于处理跨多行/列的表。行/列拆分操作还可能剪切包含多行文本的单元格。
另一组方法以自下而上的方式解决上述问题,首先检测文本块的位置,然后通过启发式规则[38]或GNN(图形神经网络)[29,14,2,24,26]恢复边界框的关系。然而,基于文本区域边界框设计的规则容易处理复杂的匹配情况。基于GNN的方法不仅带来额外的网络成本,而且还依赖于更昂贵的训练成本,如数据量。另一个问题是,这些方法很难获得空单元格,因为它们通常会陷入跨行/跨列单元格的视觉模糊问题。空单元格的预测直接影响表结构的正确性,如图1(a)所示。此外,如何分割或合并这些空白区域仍然是一个不可忽视的挑战性问题,因为当图像转换为数字格式时,不同的分割结果将生成不同的可编辑区域。
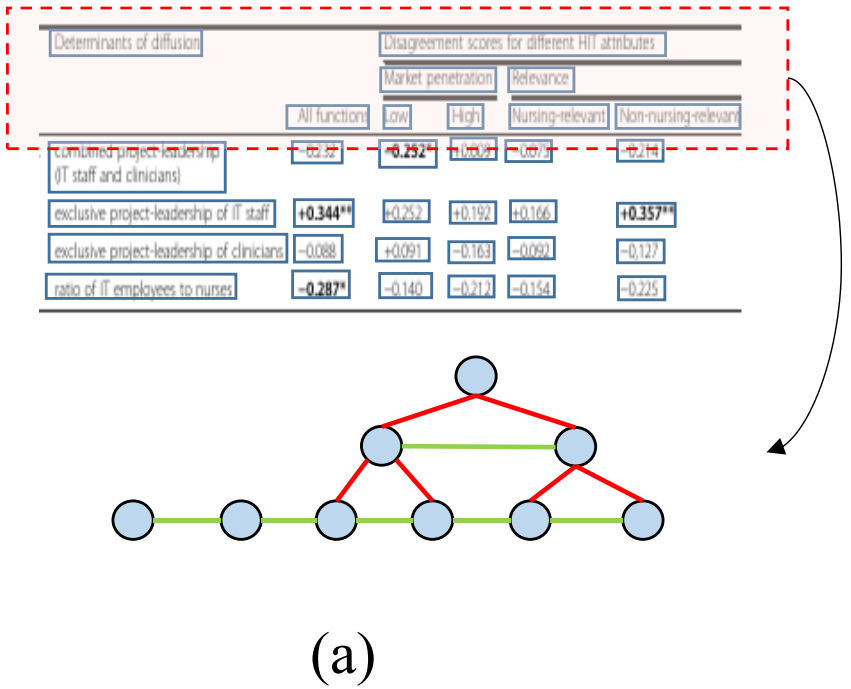
请注意,表本身的结构是一个人工生成的基于规则的数据表单。在表格没有视觉旋转或透视变换的情况下,如果我们能够获得所有完全对齐的单元格区域,而不是文本区域[26],结构推断将很容易且几乎无损,如图1(b)所示。然而,获取这些信息并不容易。一方面,文本区域[5,2,39]的注释比单元格区域更容易获得。另一方面,由于区域外围通常没有可见的边界纹理,因此很难准确地学习对齐的框。多行/列单元格很容易与空单元格区域混淆。例如,在图1(c)中,网络通常会陷入预测的对齐框不够大的情况,并导致错误的单元匹配。虽然[26]设计了一个对齐损失来帮助边界框学习,但它只考虑框之间的相对关系,无法捕获小区的绝对覆盖区域。
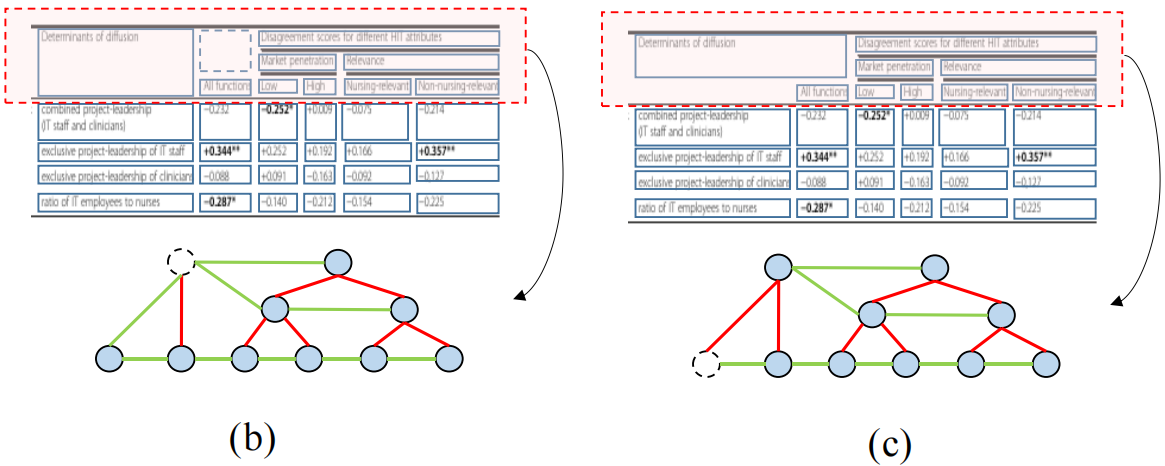
在本文中,我们的目标是训练网络以获得更可靠的对齐单元区域,并在一个模型中解决空单元的生成和划分问题。观察到人们在阅读时同时感知到来自局部文本区域和全局布局的视觉信息,我们提出了一种统一的表格结构识别框架,称为LGPMA(local and global Pyramid Mask Alignment,局部和全局金字塔掩码对齐)网络,以兼顾局部和全局信息的优点。具体而言,该模型同时学习基于局部掩码RCNN的[6]对齐边界框检测任务和全局分割任务。在这两项任务中,我们都采用了金字塔软掩码监控[17],以帮助获得更精确的对齐边界框。在LGPMA中,局部分支(LPMA)通过可见纹理感知器获得更可靠的文本区域信息,而全局分支(GPMA)可以获得更清晰的细胞范围或分裂的空间信息。这两个分支通过联合学习帮助网络更好地学习融合特征,并通过提出的掩码重新评分策略有效地细化检测到的对齐边界框。基于改进后的结果,我们设计了一个健壮、直观的表结构恢复管道,该管道可以有效地定位空单元,并根据全局分割的指导进行精确合并。
本文的主要贡献如下:
- (1)我们提出了一个新的框架,称为LGPMA网络,它从局部和全局两个角度融合了视觉特征。该模型充分利用了局部和全局特征的信息,通过提出的掩码重评分策略,可以获得更可靠的对齐细胞区域。
- (2) 我们介绍了一个统一的表结构恢复管道,包括单元匹配、空单元搜索和空单元合并。非空细胞和空细胞都能被有效定位和分裂。
- (3) 大量的实验表明,我们的方法在几个流行的基准测试上取得了有竞争力的、甚至是最先进的结果。
二、相关工作
传统的表格识别研究主要采用手工特征和启发式规则[8,10,34,19,18,3]。这些方法大多应用于简单的表结构或特定的数据格式,如PDF。关于表格检测和识别的早期技术可以在综合调查中找到[37]。随着深度神经网络在计算机视觉领域的巨大成功,人们开始关注具有更一般结构的基于图像的表格[21,30,24,9,13,36,23,14,33]。根据基本组件粒度,我们将以前的方法大致分为两类:
- 基于全局对象的方法
- 基于局部对象的方法
基于全局对象的方法主要关注全局表组件的特性,大多从行/列或网格边界检测开始。[30,31,32]的工作首先使用检测或分割模型获得行和列区域,然后将这两个区域相交以获得单元网格。[22]通过表区域掩码学习和表的行/列掩码学习,以端到端的方式处理表检测和表识别任务。[33]通过学习行/列之间的间隔区域分割,然后预测指示器合并分离的单元格,来检测行和列。
还有一些方法[13,39]直接感知整个图像信息,并在编码器-解码器框架中将表格结构输出为文本序列。虽然这些方法看起来很优雅,而且完全避免了人为因素的影响,但是这些模型通常都很难训练,并且需要依赖大量的训练数据。基于全局对象的方法通常难以处理各种复杂的表结构,例如跨多行/列的单元格或包含多行文本的单元格。
基于局部对象的方法从最小的基本元素单元开始。考虑到单元格级别的文本区域标注,文本检测任务相对容易通过Yolo[27]和更快的RCNN[28]等通用检测方法完成。之后,一组方法[36,23,38]尝试基于一些启发式规则和算法恢复单元格关系。另一类方法[11,2,14,24,26]将检测到的框视为图中的节点,并尝试基于图神经网络技术预测关系[29]。[14] 利用视觉特征、文本位置、单词嵌入等多种特征预测三类节点(水平连接、垂直连接、无连接)之间的关系[2]采用图形注意机制提高预测精度。[24]通过成对采样策略缓解了图节点数量大的问题。上述三部著作[14,2,24]也为该研究领域发布了新的表格数据集。由于没有检测到空单元,基于局部对象的方法通常陷入空单元模糊。
在本文中,我们试图兼顾全局和局部特征的优点。基于局部检测结果,我们整合了全局信息来细化检测到的边界框,并为空单元划分提供了直观的指导。
三、方法论
我们提出了模型LGPMA,其总体工作流程如图2所示。
3.1 总述
该模型是基于现有Mask RCNN[6]建立的。边界框分支直接学习非空单元对齐边界框的检测任务。网络同时学习基于RoI对齐操作提取的局部特征的局部金字塔掩码对齐(LPMA)任务和基于全局特征映射的全局金字塔掩码对齐(GPMA)任务。
在LPMA中,除了学习文本区域掩码的二值分割任务外,还使用水平和垂直方向上的金字塔软掩码监控来训练网络。
在GPMA中,网络学习所有非空单元对齐边界框的全局金字塔掩码。为了获得更多关于空单元分割的信息,网络还学习了同时考虑非空单元和空单元的全局二值分割任务。

然后采用金字塔掩码重新评分模块对预测的金字塔标签进行细化。通过平面聚类可以得到精确对齐的边界盒。最后,集成单元匹配、空单元搜索、空单元合并的统一结构恢复管道,得到最终的表结构。
3.2 检测框对齐
精确的文本区域匹配的困难主要来自文本区域与真实单元格区域之间的覆盖范围差距。实际单元格区域可能包含行/列对齐的空白,尤其是跨多行/列的单元格。受[26,36]的启发,通过文本区域和行/列索引的注释,我们可以根据每行/列中的最大框高度/宽度轻松生成对齐的边界框注释。对齐边界框的区域与实际单元的区域大致相等。对于打印格式且无视觉旋转或透视变换的表格图像,如果我们能够获得对齐的单元格区域并假设没有空单元格,则很容易根据水平和垂直方向上的坐标重叠信息推断单元格关系。
我们采用Mask-RCNN[6]作为基础模型。在边界框分支中,基于对齐的边界框监督对网络进行训练。然而,对齐边界框学习并不容易,因为单元格很容易与空区域混淆。受高级金字塔掩码文本检测器[17]的启发,我们发现使用软标签分割可以突破建议的边界框的限制,并提供更精确的对齐边界框。为了充分利用局部纹理和全局布局的视觉特征,我们建议同时学习这两个折叠中的金字塔遮罩对齐信息。
3.3 局部金字塔掩码对齐
在掩模分支中,训练模型学习二值分割任务和金字塔掩模回归任务,我们称之为局部金字塔掩模对齐(LPMA)。
二值分割任务与原始模型相同,其中只有文本区域标记为1,其他区域标记为0。检测到的遮罩区域可用于后面文本识别任务。
对于金字塔mask回归,我们在水平和垂直方向上为建议边界框区域中的像素分配软标签,如图3所示。文本的中间点将具有最大的回

归目标1。具体来说,我们假设所提出的对齐边界框(图中蓝色的框)的形状为H×W。边框(BBox:红色框)的左上角右下角分别表示为\(\{\left(x_{1},y_{1}\right) ,\left(x_{2},y_{2}\right)\}\),其中\(0\leqslant x_{1}\leqslant x_{2}\leq W\),\(0\leqslant y_{1}\leqslant y_{2}\leq H\)。因此,金字塔mask的shape=(2,H,W),训练目标值是属于\(\left[0,1\right]\)。两个通道分别表示了水平、垂直mask。对于任意像素\((h,w)\),这两个值可以由如下形式给出:
其中,\(0\leqslant w < W,0\leqslant h <H\),\(\left ( x_{mid},y_{mid} \right ) = \left ( \frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2} \right )\)。这样,建议区域中的每个像素都参与预测边界。
3.4 全局金字塔Mask对齐
虽然LPMA允许预测的掩码突破提议边界框,但局部区域的接受域是有限的。为了确定单元格的准确覆盖区域,全局特征还可能提供一些视觉线索。受[40,25]的启发,从全局视图中学习每个像素的偏移可以帮助定位更精确的边界。然而,单元级边界框的宽高比可能会发生变化,这导致了回归学习中的不平衡问题。因此,我们使用金字塔标签作为每个像素的回归目标,称为全局金字塔掩码对齐(GPMA)。
与LPMA一样,GPMA同时学习两个任务:全局分割任务和全局金字塔掩码回归任务。在全局分割任务中,我们直接分割所有对齐的单元格,包括非空单元格和空单元格。根据同一行/列中非空单元格的最大高度/宽度生成空单元格的基本真值。请注意,只有此任务才能学习空单元格分割信息,因为空单元格不可能在某种程度上影响区域建议网络的可见文本纹理。我们希望该模型能够根据人类的阅读习惯,在全局边界分割过程中捕捉到最合理的单元格分裂模式,这一点可以通过人工标注的注释反映出来。对于全局金字塔掩码回归,由于只有文本区域可以提供不同峰值的信息,因此所有非空单元格将被分配类似于LPMA的软标签。GPMA中对齐边界框的所有GT将缩小5%,以防止框重叠。
3.5 优化
目标网络是一个端到端的多优化任务网络,总优化函数可以写为:
其中的\(\mathcal{L}_{rpn},\mathcal{L}_{cls}, \mathcal{L}_{box}, \mathcal{L}_{mask}\)是和MaskRCNN相同的损失函数。\(\mathcal{L}_{seg}\)是全局二值分割损失,通过Dice系数损失实现;\(\mathcal{L}_{LPMA}\),\(\mathcal{L}_{GPMA}\)是基于像素级\(L_{1}\)损失的金字塔标签回归损失。
3.6 推理
推理过程可以分为两个阶段。我们首先根据金字塔掩码预测得到精确对齐的边界框,然后利用所提出的结构恢复管道生成最终的表结构。
边界框对齐。除了通过联合训练产生的好处外,局部和全局特征在物体感知方面也表现出各种优势[35]。在我们的设置中,我们发现局部特征预测更可靠的文本区域mask,而全局预测可以提供更可靠的远距离视觉信息。为了折衷这两种水平的优点,我们提出了一种金字塔掩码重新评分策略,以折衷LPMA和GPMA的预测。对于具有局部金字塔掩码预测的任何建议区域,我们添加来自全局金字塔掩码的信息以调整这些分数。我们使用一些动态权重来平衡LPMA和GPMA的影响。
对于一个预测的对齐边框\(B=\left \{ \left ( x_{1},y_{1} \right ),\left ( x_{2},y_{2} \right ) \right \}\),我们首先获得文本区域mask的bbox,记为:\(B_{t}=\left \{ \left ( x_{1}^{'},y_{1}^{'} \right ),\left ( x_{2}^{'},y_{2}^{'} \right ) \right \}\)。然后,我们可以在全局分割图中找到匹配的连通区域\(P=\left\{ p_{1},p_{2},\cdots ,p_{n} \right \}\),其中\(p=\left(x,y\right)\)表示像素。我们使用\(P_{o}=\left \{ p \mid x_{1}\leqslant p.x \leqslant x_{2}, y_{1}\leqslant p.y \leqslant y_{2} \right \}\)表示重叠区域。则关于点\(\left(x,y\right) \in P_{o}\)的预测金字塔标签可以由如下的方式计算:
其中\(x_{mid}=\frac{x_{1}^{'}+x_{2}^{'}}{2},y_{mid}=\frac{y_{1}^{'}+y_{2}^{'}}{2}\),\(F_{hor}^{\left ( L \right )}\left ( x,y \right )\),\(F_{hor}^{\left ( G \right )}\left ( x,y \right )\),\(F_{ver}^{\left ( L \right )}\left ( x,y \right )\),\(F_{ver}^{\left ( G \right )}\left ( x,y \right )\)分别表示局部水平、全局水平、局部垂直、全局垂直金字塔标签预测。
接下来,对于任何建议区域,可以使用水平和垂直金字塔mask标签(对应于z坐标)分别拟合三维空间中的两个平面。所有四个平面与零平面的相交线都是细化的边界。例如,要优化对齐框的右边界,我们选择所有使用优化金字塔mask预测\(F\left(x,y\right)\)进行对满足\(P_{r}=\left\{ p \mid x_{mid}\leqslant p.x \leqslant x_{2}, p\in P_{o} \right\}\)的像素拟合平面。如果我们记\(ax+by+c-z=0\),使用最小二乘法,这个问题可以转化为 最小化下面的式子:
\(a,b,c\)参数可以通过如下的矩阵计算:
其中\(\left \| P_{o} \right \|\)表示集合的大小。然后计算拟合平面与z=0平面之间的交线。假设边界框是轴对齐的,我们计算细化的\(x\)坐标作为平均值:
同样,我们可以得到其他三个细化的边界。请注意,精炼过程可以选择性地迭代进行,参见[17]。
表格结构恢复。基于精确对齐的边界框,表结构恢复管道旨在获得最终的表结构,包括三个步骤:单元匹配、空单元搜索和空单元合并,如图4所示。
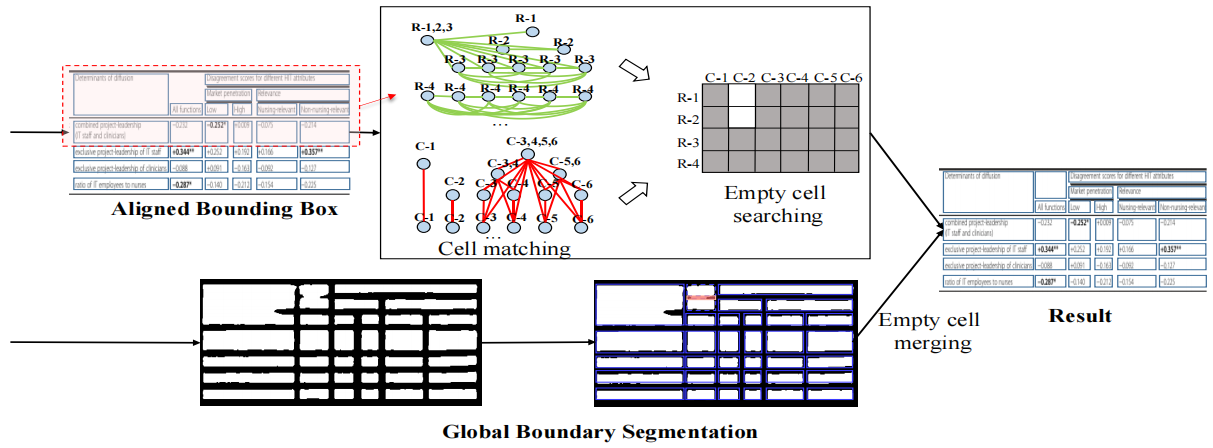
单元格匹配。(这一步相当于行列关系判断)在所有对齐的边界框都是轴对齐的情况下,单元格匹配过程非常简单,但非常健壮。按照与[14,2,24]相同的命名约定,连接关系可分为水平和垂直类型。其主要思想是,如果两个对齐的边界框在x/y坐标上有足够的重叠,我们将在垂直/水平方向上匹配它们。在数学上,对任意两个对齐边界框:\(\left \{ \left ( x_{1},y_{1} \right ), \left ( x_{2},y_{2} \right ) \right \}\)、\(\left \{ \left ( x_{1}^{'},y_{1}^{'} \right ), \left ( x_{2}^{'},y_{2}^{'} \right ) \right \}\),如果\(y_{1}^{'}\leqslant \frac{y_{1}+y_{2}}{2}\leqslant y_{2}^{'}\)或者\(y_{1}\leqslant \frac{y_{1}^{'}+y_{2}^{'}}{2}\leqslant y_{2}\),它们将水平连接。类似地如果\(x_{1}^{'}\leqslant \frac{x_{1}+x_{2}}{2}\leqslant x_{2}^{'}\)或者\(x_{1}\leqslant \frac{x_{1}^{'}+x_{2}^{'}}{2}\leqslant x_{2}\),它们将垂直连接。
空单元格搜索。在获得检测到的对齐边界框之间的关系后,我们将它们视为图中的节点,并且连接关系是边。同一行/列中的所有节点构成一个完整的子图。受[24]的启发,我们采用最大团搜索算法[1]来查找图中的所有最大团。以行搜索过程为例,属于同一行的每个节点都将位于同一个群组中。对于跨越多行的单元格,相应的节点将在不同的组中多次出现。通过平均y坐标对这些团进行排序后,我们可以很容易地用其行索引标记每个节点。出现在多个派系中的节点将使用多个行索引进行标记。我们可以很容易地找到与空单元格相对应的空缺位置。
空单元格合并。到目前为止,我们已经获得了最小级别的空单元格(占用1行1列)。为了更可行地合并这些单元格,我们首先将具有对齐边界框形状的单个空单元格指定为同一行/列中单元格的最大高度/宽度。由于全局分割任务学习到的视觉线索,我们可以根据分割结果设计简单的合并策略。我们计算每两个相邻空单元的间隔区域中预测为1的像素比率,如图4所示的红色区域。如果比率大于预设阈值,我们将合并这两个单元格。我们可以看到,空区域的视觉模糊性总是存在的,分割任务很难被完全学习。这就是为什么许多基于分割的方法[24,23,22]难以进行复杂的后处理,例如fracture completion和阈值设置。该方法直接采用全局分割提供的原始视觉线索,并使用像素投票获得更可靠的结果。
四、实验
实验嘛,就是牛皮,每个论文都是这样的!
4.1 数据集
包含文本内容边界框和单元格关系的注释。我们根据以下流行的基准评估我们提议的框架:
- ICDAR 2013[5]。该数据集包含98个培训样本和156个测试样本,这些样本取自政府报告的PDF格式。
- SciTSR[2]。该数据集包含12000张训练图像和3000张从科学文献PDF中截取的测试图像。作者还选择了一个复杂样本子集,其中包含2885个训练图像和716个测试图像,称为SciTSR COMP。
- PubTabNet[39]。这是一个大规模的复杂表格集合,包含500777个训练图像、9115个验证图像和9138个测试图像。此数据集包含大量具有多行/列单元格、空单元格等的三行表。
4.2 实验效果
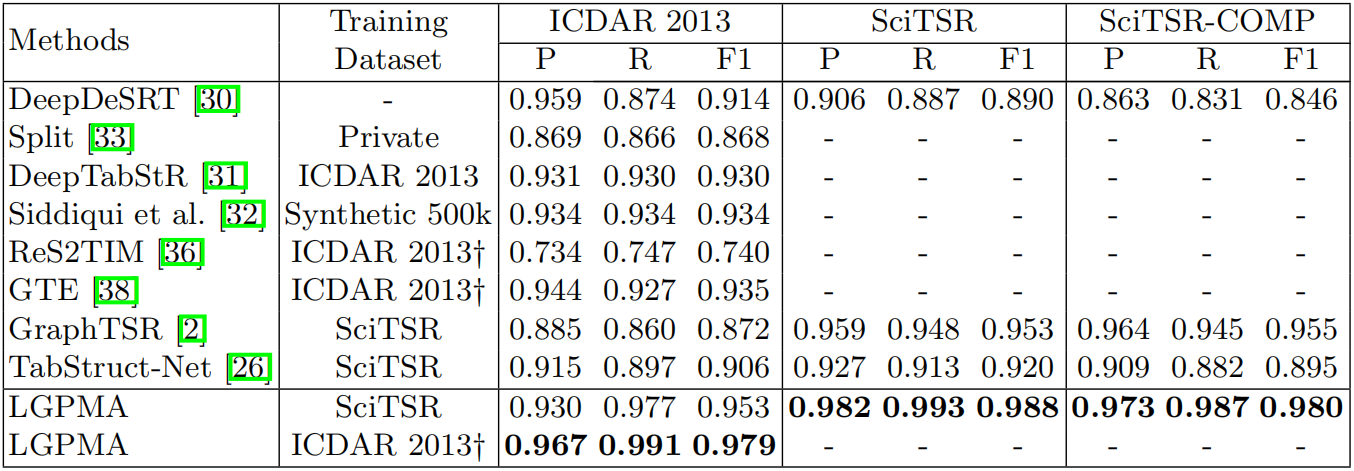
结构恢复:
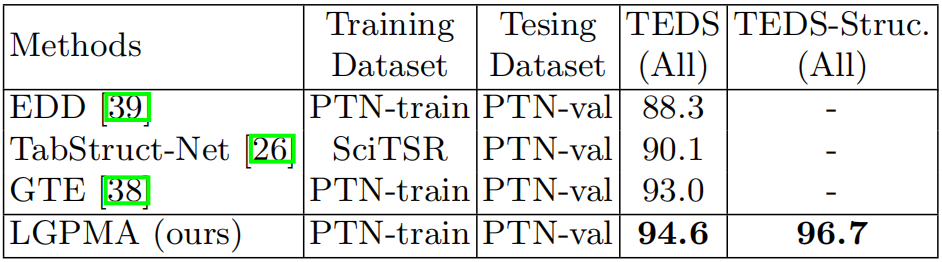
4.3 消融实验
边界框检测:
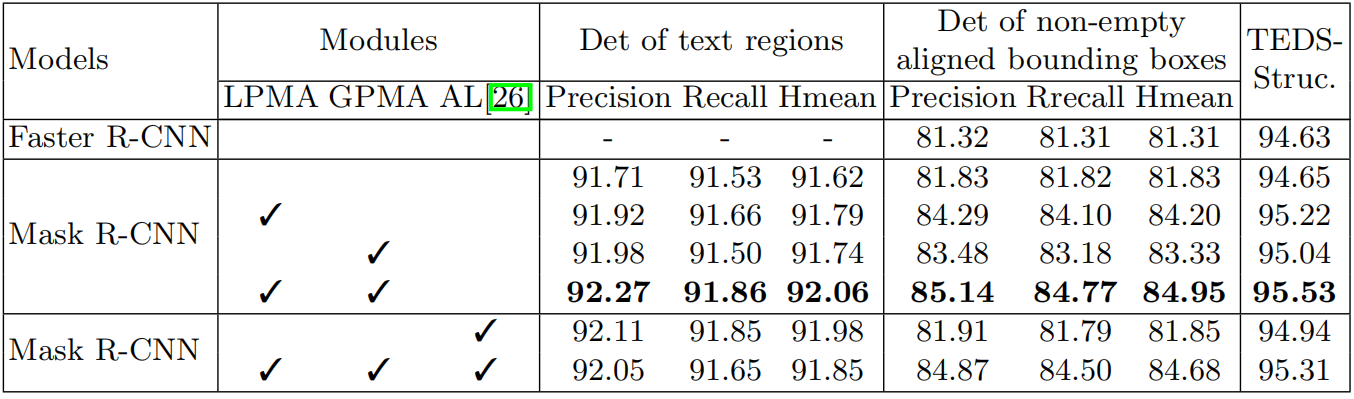
Alignment Loss:AL,明显AL与LPMA、GPMA有些冲突,所以作者没有使用!
结构恢复:
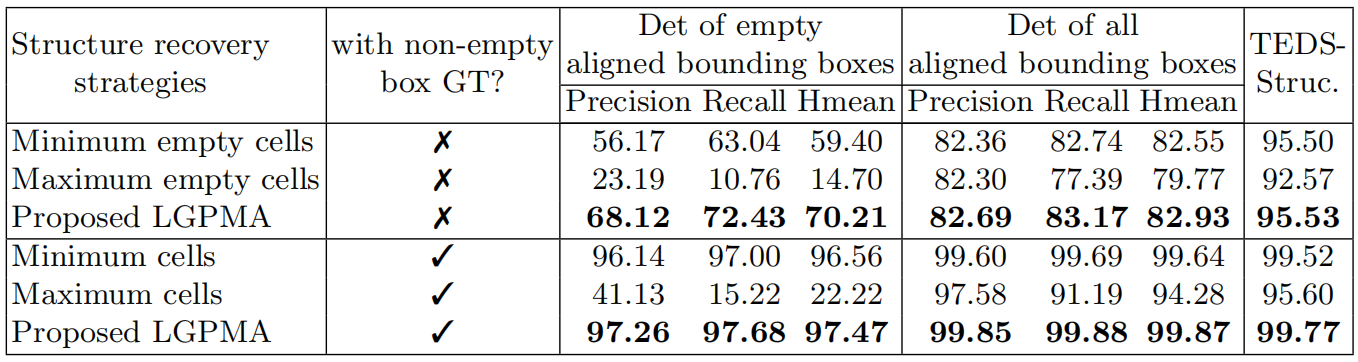
五、总结
本文提出了一种新的表结构识别框架LGPMA。我们采用局部和全局金字塔mask学习来折衷局部纹理和全局布局信息的优点。在推理阶段,通过掩码重新评分策略融合两个级别的预测,网络生成更可靠的对齐边界框。最后,我们提出了一个统一的表结构恢复管道来获得最终结果,它还可以预测可行的空单元划分。实验结果表明,我们的方法在三个公共基准中达到了最新的水平。
项目的梳理图参考:
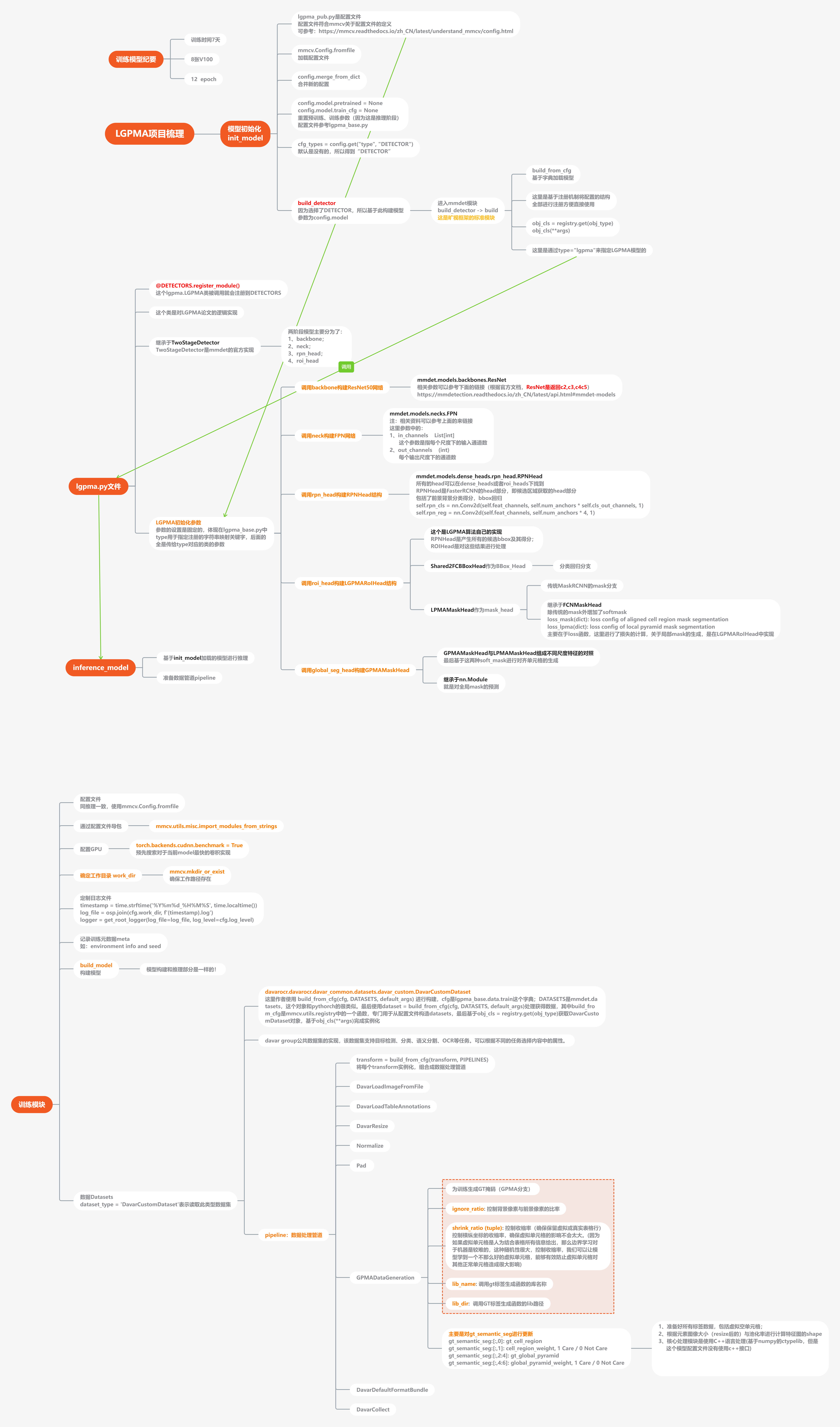
高清图片可下载查看
六、期望的数据标签
标注样例
{
"Images/train/PMC3348833_020_01.png": {
"height": 90,
"width": 395,
"content_ann": {
"bboxes": [
[40, 4, 75, 20], # 文本单元格区域的边界框. 空使用空列表[]标识.
[144, 4, 163, 20],
...
],
"cells": [
[0,0,0,0], # 行列坐标数组: [start row,start column,end row,end column]
[0,1,0,1],
...
],
"labels": [
[0], # 单元格类型标注. [0] 标识head; [1]标识 body
[0],
[0],
[0],
[1],
[1],
[1],
[1],
.....
]
}
},
}
- 每个图片都以
Images/train/PMC3348833_020_01.png的形式给出的关键字,值是一个字典; height、width分别记录高和宽;content_ann标记文本单元格相关内容- bboxes: 单元格的边框;
- cells: 单元格在表格中的坐标信息(行列坐标非像素坐标);
- labels: 单元格类型标注(0表示表格头,1表示表格体).
PubTabNet源数据格式
{
"imgid": 548625,
"html": {
"cells": [
{"tokens": []},
{"tokens": ["<b>", "W", "e", "a", "n", "i", "n", "g", "</b>"], "bbox": [66, 4, 96, 13]},
{"tokens": ["<b>", "W", "e", "e", "k", " ", "1", "5", "</b>"], "bbox": [131, 4, 160, 13]},
{"tokens": ["<b>", "O", "f", "f", "-", "t", "e", "s", "t", "</b>"], "bbox": [201, 4, 226, 13]},
{"tokens": ["W", "e", "a", "n", "i", "n", "g"], "bbox": [1, 17, 31, 26]},
{"tokens": ["–"], "bbox": [66, 21, 72, 25]},
{"tokens": ["–"], "bbox": [131, 21, 137, 25]},
{"tokens": ["–"], "bbox": [201, 21, 207, 25]},
{"tokens": ["W", "e", "e", "k", " ", "1", "5"], "bbox": [1, 31, 30, 40]},
{"tokens": ["–"], "bbox": [66, 35, 72, 39]},
{"tokens": ["0", ".", "1", "7", " ", "±", " ", "0", ".", "0", "8"], "bbox": [131, 31, 166, 40]},
{"tokens": ["0", ".", "1", "6", " ", "±", " ", "0", ".", "0", "3"], "bbox": [201, 31, 236, 40]},
{"tokens": ["O", "f", "f", "-", "t", "e", "s", "t"], "bbox": [1, 45, 26, 54]},
{"tokens": ["–"], "bbox": [66, 49, 72, 53]},
{"tokens": ["0", ".", "8", "0", " ", "±", " ", "0", ".", "2", "4"], "bbox": [131, 45, 166, 54]},
{"tokens": ["0", ".", "1", "9", " ", "±", " ", "0", ".", "0", "9"], "bbox": [201, 45, 236, 54]}],
"structure": {
"tokens": ["<thead>", "<tr>", "<td>", "</td>", "<td>", "</td>", "<td>", "</td>", "<td>", "</td>", "</tr>", "</thead>", "<tbody>", "<tr>", "<td>", "</td>", "<td>", "</td>", "<td>", "</td>", "<td>", "</td>", "</tr>", "<tr>", "<td>", "</td>", "<td>", "</td>", "<td>", "</td>", "<td>", "</td>", "</tr>", "<tr>", "<td>", "</td>", "<td>", "</td>", "<td>", "</td>", "<td>", "</td>", "</tr>", "</tbody>"]
}
},
"split": "val",
"filename": "PMC5755158_010_01.png"}
七、数据格式转换
从PubTabNet标注格式转化为 davar格式(旷视的格式):
import numpy as np
def html_to_davar(html):
""" 将PubTabNet标注格式转化为 davar格式(旷视的格式)
Args:
html (dict): "html" in original PubTabNet, which is used to describe table structure and content. For example:
"html": {
"cells": [
{"tokens": ["<b>", "T", "r", "a", "i", "t", "</b>"],
"bbox": [11, 5, 33, 14]},
{"tokens": ["<b>", "M", "e", "a", "n", "</b>"],
"bbox": [202, 5, 225, 14]},
{"tokens": ["S", "C", "S"],
"bbox": [14, 27, 30, 35]},
{"tokens": ["-", " ", "0", ".", "1", "0", "2", "4"],
"bbox": [199, 27, 229, 35]}
],
"structure": {"tokens":
["<thead>", "<tr>", "<td>", "</td>", "<td>", "</td>", "</tr>", "</thead>",
"<tbody>", "<tr>", "<td>", "</td>", "<td>", "</td>", "</tr>", "</tbody>"]
}
}
Returns:
dict: "content_ann" in ours training dataset (davar format), like:
"content_ann": {
"bboxes": [[11, 5, 33, 14],
[202, 5, 225, 14],
[14, 27, 30, 35],
[199, 27, 229, 35]],
"texts": ["Trait", "Mean", "SCS", "- 0.1024"],
"texts_tokens": [["<b>", "T", "r", "a", "i", "t", "</b>"],
["<b>", "M", "e", "a", "n", "</b>"],
["S", "C", "S"],
["-", " ", "0", ".", "1", "0", "2", "4"]],
"cells": [[0,0,0,0],
[0,1,0,1],
[1,0,1,0],
[1,1,1,1]],
"labels": [["t-head"],
["t-head"],
["t-head"],
["t-head"]]
}
"""
bboxes, texts, texts_tokens, cells, labels = [], [], [], [], [] # 初始化五个返回对象
# 基于head数量和span_matrix获取单元格和标签(标签标识head、body)
span_matrix = get_matrix(html['structure']['tokens']) # get span_matrix represent table structure
num_h, num_b = get_headbody(html['structure']['tokens']) # 获取 t-head and t-body的数量
for i in range(1, 1 + span_matrix.max()):
where = np.where(span_matrix == i)
s_r, e_r = int(where[0].min()), int(where[0].max())
s_c, e_c = int(where[1].min()), int(where[1].max())
cells.append([s_r, s_c, e_r, e_c]) # 生成表格坐标(非像素坐标)
labels.append(["t-head"]) if i <= num_h else labels.append(["t-body"])
# get bboxes, texts and texts_tokens
char_sign = [
'<b>', '<i>', '<sup>', '<sub>', '<underline>',
'</b>', '</i>', '</sup>', '</sub>', '</underline>'
]
for cell in html['cells']:
if "bbox" in cell.keys():
bboxes.append(cell["bbox"])
text = ''.join([t for t in cell["tokens"] if t not in char_sign])
texts.append(text)
texts_tokens.append(cell["tokens"])
else:
bboxes.append([])
texts.append("")
texts_tokens.append([])
content_ann = {"bboxes": bboxes, "texts": texts, "texts_tokens": texts_tokens, "cells": cells, "labels": labels}
return content_ann
def get_matrix(html_str):
"""Convert html to span matrix, a two-dimensional matrix representing table structure
Args:
html_str[list]: html representing table structure.
Returns:
np.array(num_row x num_col): span matrix
"""
# 基于html标签获取行列数量
row_index = [i for i, tag in enumerate(html_str) if tag == "<tr>"] # <tr>是换行标签
num_row = len(row_index) # 记录行的数量
num_col = 0 # 初始化列数为0
html_row0 = html_str[row_index[0]:row_index[1]] # 截取第一行所有数据
for ind, tag in enumerate(html_row0):
if "rowspan" in tag:
# 如果行列合并同时出现, 跳过当前的"rowspan"标签
if ind != len(html_row0) - 1 and "colspan" in html_row0[ind + 1]:
continue
else:
num_col += 1
elif "colspan" in tag:
num_col += int(tag[-3:-1]) if tag[-3:-1].isdigit() else int(tag[-2])
elif tag == "<td>":
num_col += 1
# 将html转换为span矩阵,一种表示table结构的二维矩阵
span_matrix = np.zeros([num_row, num_col], dtype=int) - 1
status = html_to_area(html_str, row_index, span_matrix)
if status: # 如果html是非法的,则返回零
span_matrix = np.zeros([num_row, num_col], dtype=int)
return span_matrix
def get_headbody(html_str):
"""Calculating number of bboxes belonging to "t-head" and "t-body" respectively
Args:
html_str(str): html representing table structure
Returns:
int: number of bboxes belonging to "t-head"
int: number of bboxes belonging to "t-body"
"""
s_h, e_h = html_str.index('<thead>'), html_str.index('</thead>')
s_b, e_b = html_str.index('<tbody>'), html_str.index('</tbody>')
num_h = html_str[s_h + 1:e_h].count('</td>')
num_b = html_str[s_b + 1:e_b].count('</td>')
return num_h, num_b
def html_to_area(html_str, row_index, span_matrix):
"""Convert html to span matrix, a two-dimensional matrix representing table structure
Args:
html_str(list): html representing table structure.
row_index(list): index of each row in html.
span_matrix(np.array): a two-dimensional matrix representing table structure.
Returns:
np.array(num_row x num_col): span matrix
span_matrix: shape=[num_row, num_col]的二维矩阵, 相同单元格使用通用的编号, 编号从1开始
"""
num_row, num_col = span_matrix.shape[0], span_matrix.shape[1]
status = 0 # 给定的html标签是否合法
area_index = 1
row_index.append(len(html_str))
for i in range(num_row):
col_index = 0 # 记录当前行的列标签数量
span_together = 0 # 单元格合并数量
html_cur_row = html_str[row_index[i]:row_index[i + 1]] # 第i行的所有标签
for ind, tag in enumerate(html_cur_row):
if span_together:
span_together = 0
continue
if tag != "<td>" and "span" not in tag: # 只对含有合并的<td>单元格标签进行统计
continue
if col_index > num_col - 1: # 当前行的列超过了第一行的列
return 1
while span_matrix[i, col_index] != -1: # 当前单元格是行合并单元格的一部分
if col_index == num_col - 1:
return 1
else:
col_index += 1
# basic cell
if tag == "<td>": # 无合并单元格
span_matrix[i, col_index] = area_index # 记录真实的单元格(进行了编号)
col_index += 1
# 同时有行列合并
elif "rowspan" in tag and (ind != len(html_cur_row) - 1 and "colspan" in html_cur_row[ind + 1]):
# TODO: 优化rowspan, colspan的数值, 当前只能有一位
row = int(tag[-3:-1]) if tag[-3:-1].isdigit() else int(tag[-2]) # 默认合并行数小于10
col = int(html_cur_row[ind + 1][-3:-1]) \
if html_cur_row[ind + 1][-3:-1].isdigit() else int(html_cur_row[ind + 1][-2]) #
span_together = 1 # 跳过下一个span, 因为html列表中<td>标签被拆分了: [<td, rowspan='2', colspan='3', >]
if (span_matrix[i:i + row, col_index:col_index + col] != -1).any():
return 3 # 单元格出现重叠
span_matrix[i:i + row, col_index:col_index + col] = area_index
if i + row > span_matrix.shape[0] or col_index + col > span_matrix.shape[1]:
return 2 # 合并后单元格超出了表格边界
col_index += col
elif "colspan" in tag: # 仅有列合并
col = int(tag[-3:-1]) if tag[-3:-1].isdigit() else int(tag[-2])
if col_index + col > num_col:
return 2
if (span_matrix[i, col_index:col_index + col] != -1).any():
return 3
span_matrix[i, col_index:col_index + col] = area_index
col_index += col
elif "rowspan" in tag: # 仅有行合并
row = int(tag[-3:-1]) if tag[-3:-1].isdigit() else int(tag[-2])
if i + row > num_row:
return 2
if (span_matrix[i:i + row, col_index] != -1).any():
return 3
span_matrix[i:i + row, col_index] = area_index
col_index += 1
area_index += 1
if -1 in span_matrix:
status = 1 # 某些行的列数小于第一行的列数
return status
完!


