HMM隐马尔可夫模型
隐马尔可夫
作者:elfin 参考资料来源:《统计学习方法》第二版
本文主要基于李航老师的《统计学习方法》第二版与在学校期间残留的记忆书写,如有差池,望指教!
代码开源:https://github.com/firstelfin/HMM
1、隐马尔可夫简介
在很多人看来,HMM、CRF这种传统算法很low!似乎在深度学习大行其道的年代,经典算法已经成为很多人眼中的鸡肋,只有AI才是牛掰。事实真的是这样吗?不可否认,深度学习的发展让人欣喜,其未来前景也让人期待。但是深度学习之所以火热,很大程度上是因为大数据与算力。那么在我们要解决的问题中,都有大数据支持吗?很遗憾,实际生活中并不都是这样的。
如果你深入分析近年来在深度学习上的发展,在各种trick层出不穷的同时,我们也不难看到传统经典算法的影子。马尔可夫链在统计学中是非常著名的模型,隐马尔可夫在工业应用中非常广泛。实际上这种强假设模型仍然有非常大的市场。
1.1 隐马尔可夫定义
隐马尔可夫模型 隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测序列的状态随机序列,再由各个状态生成一个观测从而产生观测随机序列的过程。
- 隐藏的马尔可夫链随机生成的状态的序列,称为状态序列;
- 每个状态生成一个观测,而由此产生的观测的随机序列,称为观测序列。
序列的每一个位置可以看作一个时刻,所以是关于时序的概率模型。
1.2 隐马和马的区别
马尔可夫链常伴随齐次性假设,模型关心的是状态转移概率矩阵和初始的状态分布\(\Pi\)。直观上马尔可夫链是一个串行结构,没有分支,一条路走到黑的生成模型。它的状态是可观测的,这很重要,因为是否可观测是两者间的一个本质区别。
隐马尔可夫模型在关注状态转移概率矩阵、初始的状态分布\(\Pi\)的基础上,还关注观测概率矩阵。从结构上,两者的主要差异是隐马尔可夫除隐状态的直链结构以外还有分支,用于观测状态的展示。

1.3 隐马尔科夫模型的基本假设
假设1:齐次马尔可夫性假设(齐次性假设)。即假设隐藏的马尔可夫链在任意时刻\(t\)的状态只依赖于前一时刻的状态,与其他时刻的状态及观测无关,也与时刻\(t\)无关:
假设2:观测独立性假设。即假设人员时刻的观测只依赖于该时刻的马尔科夫链的状态,于其他观测及状态无关:
1.4 符号说明
-
\(Q= \left\{ q_{1},q_{2},\cdots,q_{N} \right\}\) 所有状态的集合;
-
\(V= \left\{ v_{1},v_{2},\cdots,v_{M} \right\}\) 所有观测的集合;
-
\(I = \left\{ i_{1},i_{2},\cdots,i_{T} \right\}\) 长度为\(T\)的隐状态序列;
-
\(O = \left\{ o_{1},o_{2},\cdots,o_{T} \right\}\) 对应的观测序列;
-
\(A = \left [ a_{ij} \right ]_{N\times N}\) 状态转移概率矩阵;
-
\(a_{ij}=P\left ( i_{t+1}=q_{j} | i_{t}=q_{i} \right ),\quad i=1,2,\cdots ,N;\quad j=1,2,\cdots ,N\)
\(t\)时刻处于状态\(q_{i}\),下一时刻处于\(q_{j}\)的概率。
-
\(B=\left [ b_{j}\left ( k \right ) \right ]_{N\times M}\) 观测的概率矩阵;
-
\(b_{j}\left ( k \right ) = P\left ( o_{t}=v_{k} | i_{t}=q_{j} \right ),\quad k=1,2,\cdots ,M; \quad j=1,2,\cdots ,N\)
在\(t\)时刻处于状态\(q_{j}\)下生成观测\(v_{k}\)的概率;
-
\(\Pi=(\pi_{1},\pi_{2},\cdots,\pi_{N})\) 初始状态概率向量。
因此一个隐马尔可夫模型可以表示为:
2、隐马尔可夫案例
2.1 案例描述
案例描述:假设在某赌场有三颗骰子,其中一颗是正常的,另外两颗被做了手脚,其投掷点数的概率如图所示:
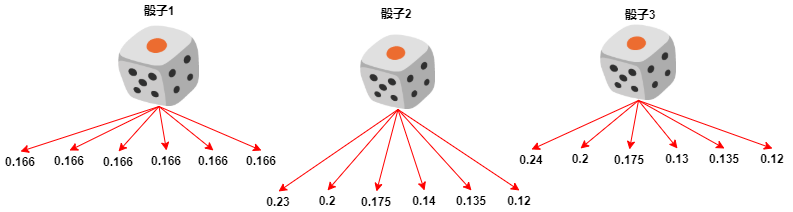
现在有一个荷官在控场,他需要从三个色子中选择一个色子进行投掷,产生骰子的观测序列:
-
开始,随机从色子中选取一个色子,进行投掷,记录其点数后放回,等待下一次投掷;
-
然后,再选择一个色子。选取的规则是:
- 若当前投掷的色子是骰子1,那么下一次一定拿骰子2;
- 若当前投掷的色子是骰子2,那么下一次各个骰子选择的概率分别为\(\left( 0.2,0.35,0.45 \right)\);
- 若当前投掷的色子是骰子3,那么下一次各个骰子选择的概率分别为\(\left( 0.4,0.14,0.46 \right)\);
-
确定使用的色子后,再次进行投掷,记录其点数后,放回;
-
重复上面的操作过程6次,得到一个观测序列:
\(O=\left( 6,3,1,2,4,2 \right)\)
整个过程玩家只能看见色子的点数,看不见是否更换色子。
这个案例中,有两个随机序列。第一个是骰子的序列;第二个是骰子投掷的点数序列。第一个序列是隐藏的,后者是可见的。这就是一个简单的隐马尔可夫案例。
2.2 案例的主要参数
根据前面的案例说明,下面我们梳理出,骰子造假案的主要参数。
隐马的状态集合\(Q\):
隐马的观测集合\(V\):
初始概率分布:
状态转移概率矩阵:
观测概率矩阵为:
3、隐马尔可夫的三个基本问题
经过第一章与第二章,我们对隐马尔可夫的观测序列生成应该有大概的了解了。在隐马尔可夫模型中有三个需要解决的问题。下面先分布简介。
3.1 概率计算问题
对于给定的模型 \(\lambda = \left( A,B,\Pi \right)\) 和观测序列 \(O = \left\{ o_{1},o_{2},\cdots,o_{T} \right\}\),计算在模型\(\lambda\)下观测序列\(Q\)出现的条件概率\(P \left( O|\lambda \right)\)。
3.2 学习问题
已知观测序列 \(O = \left\{ o_{1},o_{2},\cdots,o_{T} \right\}\)估计模型 \(\lambda = \left( A,B,\Pi \right)\) 参数,使得在该模型下观测序列的条件概率\(P \left( O|\lambda \right)\)最大。这种问题我们自然想到极大似然的思想来解决问题。
3.3 预测问题
预测问题,也即解码问题。对给定的观测序列,求最有可能的状态序列。已知模型 \(\lambda = \left( A,B,\Pi \right)\) 和观测序列 \(O = \left\{ o_{1},o_{2},\cdots,o_{T} \right\}\),求对给定观测序列,条件概率\(P \left( I|O \right)\)最大的状态序列\(I = \left\{ i_{1},i_{2},\cdots,i_{T} \right\}\)。
4、概率计算方法
根据模型假设,对于观测序列,我们可以穷举所有状态序列,但是这里的情况是一个组合排列问题,计算量非常大。计算复杂度为\(O\left( TN^{T} \right)\),明显这个复杂度是很大的,不适合我们用于计算较长、复杂的隐马尔可夫模型,下面将介绍著名的forward-backward algorithm。
4.1 前向算法
前向概率 给定隐马尔可夫模型\(\lambda\),定义到时刻\(t\)部分观测序列为\(o_{1},o_{2},\cdots,o_{t}\)且状态为\(q_{i}\)的概率记为前向概率,记作:
当我们知道时刻\(t\)的所有前向概率分布,则计算\(t+1\)时刻就非常简单了。对于某个状态\(q_{i}\)生成某一个观测,我们只需要从时刻\(t\)的所有状态分别乘以此状态转移到目标状态\(q_{i}\)的转移概率,再乘以观测出现的概率,最后求和,这样就可以得到在\(t+1\)时刻的状态\(q_{i}\)的前向概率。
随着时刻\(t\)的推进,最终我们可以直接求得\(P\left ( O|\lambda \right )=\sum_{i=1}^{N}\alpha_{T}\left ( i \right )\)。
可以理解为:
- 根据初始化求第一次投掷色子的前向概率分布;
- 第二次取状态\(q_{i}\),产生观测\(o_{t}\)的前向概率可以有状态转移矩阵与观测概率矩阵求得;
- 则第二次投掷的前置概率分布可以由第二步类似求得;
- 递归上面的2、3步可求\(t\)时刻的前置概率分布;
- 最后可以求得\(P\left ( O|\lambda \right )=\sum_{i=1}^{N}\alpha_{T}\left ( i \right )\)。
观测序列概率的前向算法
输入:隐马尔可夫模型\(\lambda\),观测序列\(O\)。
输出:观测序列概率\(P\left ( O|\lambda \right )\)。
-
初始值
\(\alpha_{1} \left ( i \right )=\pi _{i}b_{i}\left ( o_{1} \right ), \quad i=1,2,\cdots ,N\)
-
递归 对\(t=1,2,\cdots,T-1\)
\(\alpha_{t+1}\left ( i \right )=\left [ \sum_{j=1}^{N}\alpha_{t}\left ( j \right )\alpha_{ji} \right ]b_{i}\left ( o_{t+1} \right ),\quad i=1,2,\cdots ,N\)
-
终止
\(P\left ( O|\lambda \right )=\sum_{i=1}^{N}\alpha_{T}\left ( i \right )\)
上面我从三个角度进行了解释,对前向概率的计算应该比较清楚了,下面给出插图方便理解。
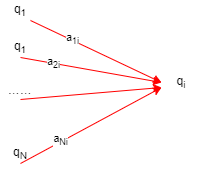
这样进行局部计算推广到全局的思想经常被使用,从时刻\(t\)到时刻\(t+1\)需要计算多少次?在\(t+1\)的每个状态都有和前一时刻的所有前向概率相乘,所以往下推一个时刻的计算复杂度为\(O\left( N^{2} \right)\),总共有\(T\)个时刻,所以计算复杂度为\(O\left( N^{2}T \right)\)。这个复杂度可比直接计算要小很多了。
4.2 前向概率案例计算
如第二章所示,假设我们想得到观测\(O=\left( 6,3,1,2,4,2 \right)\)。其他参数可[参考2.2](#2.2 案例的主要参数)。此时根据这些前提假设我们来计算\(P\left ( O|\lambda \right )\)。为了方便显示,所有小数我都保留四位。
4.2.1 数值计算
第一步:计算初值
这里的状态有三个,分别为:骰子1、骰子2、骰子3,为了方便我们使用1、2、3进行代替。
其中\(\alpha_{1} \left ( i \right )\)表示在\(1\)时刻由状态\(i\)生成观测\(o_{1}\)的概率。
第二步:递归计算
这里我们要借助4.1节中所诉的计算伪代码进行递归计算。
计算到这里,不难发现,假设我们使用\(\alpha_{t}=\left[\alpha_{t}\left( 1\right),\alpha_{t}\left( 2\right), \alpha_{t}\left( 3\right)\right]\)表示在时刻 \(t\) 的前向概率分布,延续[2.2节中的符号](#2.2 案例的主要参数)表示,\(A\)是状态概率转移矩阵,\(B\)是观测概率矩阵,那么 \(t+1\)时刻的前向概率分布为:
其中,\({}'\)表示转置,因为使用\(T\)容易造成误解;\(index(o_{t+1})\)表示观测\(o_{t+1}\)所在列的索引。
第三步:终止计算
根据上述过程即可得到:
4.2.2 代码实现
这里我们要一直迭代,手推还是比较麻烦的,这里我们借助python代码实现:
import numpy as np
A = np.array([
[0, 1, 0],
[0.2, 0.35, 0.45],
[0.4, 0.14, 0.46]
])
B = np.array([
[1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6],
[0.23, 0.2, 0.175, 0.14, 0.135, 0.12],
[0.24, 0.2, 0.175, 0.13, 0.135, 0.12]
])
class HMM(object):
"""
隐马尔可夫模型
:param transformer: 状态转移概率矩阵
:param observation: 观测概率矩阵
:param pi: 初始状态分布
"""
def __init__(self, transformer, observation, pi):
self.transformer = transformer
self.observation = observation
self.pi = pi
def forward_prob(self, last_forward, observation):
"""
计算时刻t的前向概率分布
:param last_forward: 上一时刻的概率分布
:param observation: 观测概率向量
:return: 当前的前向概率分布
"""
res = np.dot(last_forward, self.transformer) * observation
return res
def forward_prob_distribution(self, observe_seq):
"""
计算观测序列出现的概率
:param observe_seq: 观测序列
:return: 前向概率分布
"""
last_prob = self.pi * self.observation[:, observe_seq[0] - 1]
for v in observe_seq[1:]:
last_prob = self.forward_prob(last_prob, self.observation[:, v - 1])
return last_prob
def get_forward_prob(self, observe_seq):
"""
计算观测序列出现的概率
:param observe_seq: 观测序列
:return: 观测序列的概率值
"""
last_prob = self.forward_prob_distribution(observe_seq)
return np.sum(last_prob)
if __name__ == '__main__':
hmm = HMM(A, B, [1/3, 1/3, 1/3])
print(result)
上面的代码及其计算结果是否是正确的呢?
我们以《统计学习方法》第二版书上的案例来验证 (p200)。
A = np.array([
[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]
])
B = np.array([
[0.5, 0.5],
[0.4, 0.6],
[0.7, 0.3]
])
result = hmm.get_forward_prob([6, 3, 1, 2, 4, 2])
hmm = HMM(A, B, [0.2, 0.4, 0.4])
result = hmm.get_forward_prob([1, 2, 1])
最终计算结果为:0.130218;书上的结果为0.13022。两者是一致的,对比发展矩阵运算简单快捷。由公式(10、12、13)就可搞定前向概率计算。
4.3 后向算法
后向概率 给定隐马尔可夫模型\(\lambda\),定义在时刻 \(t\) 状态为 \(q_{i}\) 的条件下,从 \(t+1\) 到 \(T\) 的部分观测序列为 \(o_{t+1},o_{t+2},\cdots,o_{T}\) 的概率为后向概率,记作:
观测序列概率的后向算法
输入: 隐马尔可夫模型\(\lambda\),观测序列\(O\);
输出: 观测序列概率\(P\left ( O|\lambda \right )\)。
-
初始值:
\[\beta_{T}\left ( i \right )=1,\quad i=1,2,\cdots ,N \] -
递归: 对\(t=T-1,T-2,\cdots,1\)
\[\beta_{t}\left ( i \right )=\sum_{j=1}^{N}a_{ij}b_{j}\left ( o_{t+1} \right )\beta_{t+1}\left ( j \right ),\quad i=1,2,\cdots ,N \] -
终止:
\[P\left ( O|\lambda \right )=\sum_{j=1}^{N}\pi_{i}b_{i}\left ( o_{1} \right )\beta_{1}\left ( i \right ) \]
关于后向算法的大白话 实际就是已经求得\(t+1\)时刻之后的后向概率分布,求\(t\)时刻的后向概率分布。在\(t\)时刻,如果状态为\(q_{i}\),那么下一时刻它可能会转化为任意状态,所以(16)中对\(j\)进行了求和;而对于下一个时刻状态如果为\(j\),那么从当前状态转移过去的概率为\(a_{ij}\) 生成观测\(o_{t+1}\)的概率为\(b_{j}\left ( o_{t+1} \right )\)。
4.4 后向概率案例计算
这里我们还是以上面的案例为准,进行后向概率计算,观察结果是否一致。
如前向算法,我们可以将递归过程写为:
4.4.1 代码实现
def backward_prob(self, last_backward, observation):
"""
计算时刻t的后向概率分布
:param last_backward: 下一时刻的概率分布
:param observation: 观测概率向量
:return: 当前的后向概率分布
"""
return np.dot(self.transformer, observation * last_backward)
def backward_prob_distribution(self, observe_seq):
"""
计算观测序列出现的概率
:param observe_seq: 观测序列
:return: 后向概率分布
"""
last_backward = np.array([1] * self.transformer.shape[0])
observe_seq.reverse()
for v in observe_seq[:-1]:
last_backward = self.backward_prob(last_backward, self.observation[:, v - 1])
return last_backward
def get_backward_prob(self, observe_seq):
"""
计算观测序列出现的概率
:param observe_seq: 观测序列
:return: 观测序列的概率值
"""
last_backward = self.backward_prob_distribution(observe_seq)
return np.sum(self.pi * self.observation[:, observe_seq[-1] - 1] * last_backward)
4.4.2 代码测试
if __name__ == '__main__':
hmm = HMM(A, B, [1/3, 1/3, 1/3])
result = hmm.get_forward_prob([6, 3, 1, 2, 4, 2])
print(result)
result = hmm.get_backward_prob([6, 3, 1, 2, 4, 2])
print(result)
输出的结果:
if __name__ == '__main__':
# A B换成书上的相应矩阵
hmm = HMM(A, B, [0.2, 0.4, 0.4])
result = hmm.get_forward_prob([1, 2, 1])
print(result)
result = hmm.get_backward_prob([1, 2, 1])
print(result)
输出的结果:

以上,前向算法与后向算法结论完全一致!
4.5 前向--后向概率计算方法
对于时刻\(t\)和时刻\(t+1\),如果我们分布知道前向概率分布与后向概率分布,则观测序列的条件概率为:
上式对任意满足条件的时刻都成立,注意这里的\(t\)没有求和,只是随意取一个即可!
4.5.1 前向--后向计算代码
在HMM对象的基础上,我们实现前向后向计算方法:
def get_forward_backward_prob(self, observe_seq, split_index=1):
"""
同时使用前向--后向概率计算观测的条件概率
:param observe_seq: 观测序列
:param split_index: 切割的时刻, 这个时刻默认分配给前向算法
:return: 观测序列的条件概率
"""
assert split_index < len(observe_seq), \
"Expect split_index to be less than the length of observe_seq."
forward_distribution = self.forward_prob_distribution(observe_seq[:split_index])
backward_distribution = self.backward_prob_distribution(observe_seq[split_index:])
res = np.dot(
forward_distribution,
np.dot(self.transformer,
self.observation[:, observe_seq[split_index] - 1] * backward_distribution)
)
return res
4.5.2 代码验证
if __name__ == '__main__':
hmm = HMM(A, B, [1/3, 1/3, 1/3])
result = hmm.get_forward_prob([6, 3, 1, 2, 4, 2])
print(result)
result = hmm.get_backward_prob([6, 3, 1, 2, 4, 2])
print(result)
result = hmm.get_forward_backward_prob([6, 3, 1, 2, 4, 2], 3)
print(result)
输出结果:

这里我们使用三种方式计算的值一模一样,说明计算方式、代码实现是对的!
注:代码实现是在回顾的过程中纯手敲(没有注重代码的计算效率),如果您有优化方案,不妨留言讨论。
4.6 一些概率与期望值的计算
利用前向概率、后向概率可以获取关于单个状态和两个状态概率的计算公式。
4.6.1 给定观测\(t\)时刻状态为\(q_{i}\)的概率
对于给定的模型\(\lambda\) 和观测序列\(O\),在时刻\(t\)处于状态\(q_{i}\)的概率为:
同时,我们知道在时刻\(t\)前向概率\(\alpha_{t}(i)\)表示在时刻\(t\)的状态为\(q_{i}\)(你也可以理解为状态\(i\),这里两者可以等价);后向概率\(\beta_{t}(i)\)表示在时刻\(t\)的状态为\(q_{i}\)。那么,如果已知观测序列,有:
所以:
代码实现:
def get_qi2t_prob(self, observe_seq, t, qi):
"""
对于给定隐马尔可夫模型与观测序列,计算在时刻t处于状态qi的概率
:param observe_seq: 观测序列
:param t: 时刻的编码, [默认从1开始编码]
:param qi: 状态的编码, [默认从1开始编码]
:return: 概率值
"""
forward_distribution = self.forward_prob_distribution(observe_seq[:t])
backward_distribution = self.backward_prob_distribution(observe_seq[t-1:])
res = forward_distribution[qi-1] * backward_distribution[qi-1]\
/ np.dot(forward_distribution, backward_distribution)
return res
案例计算:
在上述案例中,计算时刻3,计算使用骰子2的概率?
result = hmm.get_qi2t_prob([6, 3, 1, 2, 4, 2], 3, 2)
print(result)
Out[1]:
0.427265264306416
上面的代码块表明,时刻3使用骰子2的概率为\(42.73\%\)。
4.6.2 给定观测时刻\(t\)状态为\(q_{i}\),时刻\(t+1\)为\(q_{j}\)的概率
对于给定的模型\(\lambda\) 和观测序列\(O\),在时刻\(t\)处于状态\(q_{i}\),且下一时刻为\(q_{j}\)的概率为:
分母是一致的,我们不需要对分母做特殊处理,只需关注分子的计算。(李教授将分子分母的形式写成一样,这样方便学生理解记忆,这里我们就不再展开了)
代码实现:
def get_qi2t_qj2next_prob(self, observe_seq, t, qi, qj):
"""
对于给定隐马尔可夫模型与观测序列,计算在时刻t处于状态qi,且下一时刻处于qj状态的概率
:param observe_seq: 观测序列
:param t: 时刻的编码, [默认从1开始编码]
:param qi: t时刻状态的编码, [默认从1开始编码]
:param qj: t+1时刻状态的编码, [默认从1开始编码]
:return: 概率值
"""
forward_distribution = self.forward_prob_distribution(observe_seq[:t])
backward_distribution = self.backward_prob_distribution(observe_seq[t:])
denominator = np.dot(
forward_distribution,
np.dot(self.transformer,
self.observation[:, observe_seq[t] - 1] * backward_distribution)
)
numerator = forward_distribution[qi - 1] * self.transformer[qi - 1, qj - 1] * self.observation[
qj - 1, observe_seq[t] - 1] * backward_distribution[qj - 1]
return numerator / denominator
4.6.3 给定观测下出现状态\(i\)的期望
代码实现:
def expect_i_appear_trans(self, observe_seq, qi, transfer=False):
"""
在观测O下, 计算状态qi出现的概率
:param observe_seq: 观测序列
:param qi: 状态的编码, [默认从1开始编码]
:param transfer: 是否由状态qi转移, 默认False
:return: 概率值
"""
res = 1
for t in range(1, len(observe_seq)):
res *= 1 - self.get_qi2t_prob(observe_seq, t, qi)
if not transfer:
res *= 1 - self.get_qi2t_prob(observe_seq, len(observe_seq), qi)
return 1 - res
这一节的公式在书本上是直接相加,我们回顾一下对于给定的模型\(\lambda\) 和观测序列\(O\),在时刻\(t\)处于状态\(q_{i}\)的概率为\(\gamma_{t}\left ( i \right )\),在\(t\)时刻处于状态\(q_{i}\),这个事件中可能包括了其他时刻也处于状态\(q_{i}\)。如果我们直接对时刻进行求和,出现的概率就会重复计算,导致出现超过1的期望值。
4.6.4 给定观测下由状态\(i\)转移的期望
这里和上面的差异很小,只需将上面的代码形参transfer指定为True即可。
A = np.array([
[0, 1, 0],
[0.2, 0.35, 0.45],
[0.4, 0.14, 0.46]
])
B = np.array([
[1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6],
[0.23, 0.2, 0.175, 0.14, 0.135, 0.12],
[0.24, 0.2, 0.175, 0.13, 0.135, 0.12]
])
hmm = HMM(A, B, [1 / 3, 1 / 3, 1 / 3])
result = hmm.expect_i_appear_trans([6, 3, 1, 2, 4, 2], 3, True)
print(result)
------------------------------------------------------------
Out[0]:
0.8718306572257475
------------------------------------------------------------
result = hmm.expect_i_appear_trans([6, 3, 1, 2, 4, 2], 3)
print(result)
------------------------------------------------------------
Out[0]:
0.9155699657722511
------------------------------------------------------------
4.6.5 给定观测下由状态\(i\)转移到状态\(j\)的期望
代码实现:
def expect_i2j(self, observe_seq, qi, qj):
"""
在观测O下, 计算状态转移的概率
:param observe_seq: 观测序列
:param qi: 状态的编码, [默认从1开始编码]
:param qj: 状态的编码, [默认从1开始编码]
:return: 概率值
"""
res = 1
for t in range(1, len(observe_seq)):
res *= 1 - self.get_qi2t_qj2next_prob(observe_seq, t, qi, qj)
return 1 - res
使用:
A = np.array([
[0, 1, 0],
[0.2, 0.35, 0.45],
[0.4, 0.14, 0.46]
])
B = np.array([
[1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6],
[0.23, 0.2, 0.175, 0.14, 0.135, 0.12],
[0.24, 0.2, 0.175, 0.13, 0.135, 0.12]
])
hmm = HMM(A, B, [1 / 3, 1 / 3, 1 / 3])
result = hmm.expect_i2j([6, 3, 1, 2, 4, 2], 2, 3)
print(result)
------------------------------------------------------------
Out[0]:
0.6501034848435623
------------------------------------------------------------
5、隐马尔可夫的学习问题
已知观测序列 \(O = \left\{ o_{1},o_{2},\cdots,o_{T} \right\}\)的集合估计模型 \(\lambda = \left( A,B,\Pi \right)\) 参数,使得在该模型下观测序列的条件概率\(P \left( O|\lambda \right)\)最大。也就是说已知观测序列,我们要学习一个隐马尔可夫模型,主要是要评估出三个参数\(A,B,\Pi\),使得当前事件发生的概率是最大的,明显这就是极大似然。关于学习方法,我们主要叙述:极大似然估计、Baum-Welch算法(鲍姆·韦尔奇算法;实际就是EM算法)。
5.1 监督学习算法
首先,我们假设有大量的观测 \(O = \left\{ o_{1},o_{2},\cdots,o_{T} \right\}\),且观测的产生模式与隐马尔可夫的模式相同。
5.1.1 状态转移概率矩阵
这里的主要思路是基于数据出现的频次分布进行参数估计,也是统计学最原始的方法。限于篇幅与性能,这里不展开这种参数估计的方法,我们重点介绍Baum-Welch方法。
5.2 鲍姆·韦尔奇算法
首先回顾EM算法,简单来说就是对参数求期望,再对期望取最大值,如此循环直到模型收敛。
此时,我们没有监督信息(状态序列),我们要学习隐马尔可夫模型的参数\(A,B,\Pi\),将观测序列记作\(O\),状态序列记为不可观测的隐数据\(I\),则我们得到:
HMM结构示意图:

5.2.1 引入目标函数
这里我们还是要使用到极大似然的思想,目标函数以对数似然函数为对象。
- 观测数据:\(O = \left\{ o_{1},o_{2},\cdots,o_{T} \right\}\)
- 隐藏数据:\(I \ = \left\{ i_{1},i_{2},\cdots,i_{T} \right\}\)
- 完全数据:\(\left(O,I \right) = \left\{ o_{1},o_{2},\cdots,o_{T},i_{1},i_{2},\cdots,i_{T} \right\}\)
- 目标函数: $ \text{log}P \left( O,I| \lambda \right)$
5.2.2 EM算法的E步:求Q函数
其中\(\bar{\lambda}\)是当前的HMM模型估计值,\(\lambda\)是要求的期望(极大化)隐马尔可夫模型参数。
目标函数--对数似然概率:
式(28)是可以由齐次性假设和观测独立性假设得到的。
Q函数可以写成:
将式(28)带入式(27)有:
(29)式是将式(28)带入式(27),把\(\text{log}\)里面的部分拆开。上式明显被分为了三部分,第一部分是关于初始状态概率分布;第二部分是状态转移概率矩阵元素;第三部分是关于观测概率矩阵元素。这正好对应了隐马尔可夫模型的三个参数。
5.2.2.1 E步总结
至此,EM算法的E步就完了。E步简单的说可以理解为求期望,那这里的Q函数怎么是期望呢?
- 首先,我们看\(P\left(O,I|\bar{\lambda} \right)\)表示什么?这个概率表示在当前模型估计下,观测状态\(O\)对应的隐状态为\(I\)的概率。
- 其次,我们思考\(\text{log}P \left( O,I| \lambda \right)\)表示什么?这个值难道不是表示我们在模型\(\lambda\)下,观测观测状态\(O\)对应的隐状态为\(I\)的对数似然概率嘛,也即这个值表示了我们目标函数的一个取值。
- 最后,我们看求和符号。将所有取值乘以其出现概率再求和,这不就是期望吗?这里的期望是对数似然的期望!
注意:很多时候我们在网上看见的公式(27)很容易以为是对\(P\left(O,I|\lambda \right)P\left(O,I|\bar{\lambda} \right)\)求对数,这里是一个书写上容易引起的误区。所以这里我们使用\(*\)号进行了分离。
5.2.3 EM算法的M步:求一组参数\(A,B,\Pi\)极大化期望
在5.2.2节中,期望\(Q\)已经被拆分为关于参数\(A,B,\Pi\)的三项了,所以我们可以分别求其最大值。
5.2.3.1 初始状态分布的M步估计
关于初始隐藏状态的分布\(\Pi\)的期望为:
回顾一下:\(\Pi=(\pi_{1},\pi_{2},\cdots,\pi_{N})\) ,这里未知参数 有\(N\)个,对于给定的\(i\),\(P\left(O,i_{1}=i|\bar{\lambda} \right)\)是一个常数。
所以,上式右边是关于\(\Pi\)的一个函数,函数如何求极值?求导,导数为零的点就是取极值的点,这个点就是参数的估计!但是我们知道概率分布,概率之和应该为1,也即:\(\sum_{i=1}^{N}\pi_{i}=1\)。所以这里是带约束的求极值问题,我们常用的方法为拉格朗日乘数法。
拉格朗日函数:
从数学的角度看式(30)与式(31)的表示是完全等价的,因为约束条件的存在!那么为什么我们要给新增项乘以\(\gamma\)呢?这里就涉及到法线的问题,因为目标函数取极值时,一定是两个函数相切的位置(两个函数分别指:目标函数;由约束条件得到的函数 $\sum_{i=1}^{N}\pi_{i}-1 $ )。因为相切,所以发现平行,法线向量差一个 \(\gamma\) 的关系。求极值我们的处理手段是求导,导数为零的点取到极值,所以乘一个常数使得法线向量相减为零的假设与求导为零的处理手段一致。
那么求导就得到法线了?是的,求导就可以得到法线。对于一个一般函数\(f(x_{1},x_{2},\cdots,x_{l})\),则它的法向量可以表示为:\(\left [ \frac{\partial f}{\partial x_{1}}, \frac{\partial f}{\partial x_{1}},\cdots , \frac{\partial f}{\partial x_{l}} \right ]\)。
也就是说拉格朗日函数求导为零的点,是这个函数的的极值,同时也是目标函数与约束函数相切的点,所以也是目标函数的极值!如何约束条件有好几个,那不就不存在相切的点?是的,但是目标函数极值点的法向量 与 每个约束函数的法向量的和向量 也必然存在\(\gamma\)倍的关系。图示理解参考见 https://www.zhihu.com/question/38586401 。
拉格朗日函数求解:
上式最后一行是对\(i\)求和得到。
初始状态分别的估计:
根据上诉求解有:
这个公式从世俗的角度也好理解。
5.2.3.2 状态概率转移矩阵的M步估计
关于状态概率转移矩阵的期望为:
注意,这里也有约束条件,而且有\(N\)个,\(\sum_{j=1}^{N}a_{ij}=1\)。
拉格朗日函数求解:
所以状态概率转移矩阵的估计为:
5.2.3.3 观测概率矩阵的M步估计
观测概率矩阵相关的期望项为:
注意,这里同样有\(N\)个约束,\(\sum_{k=1}^{M}b_{j}\left( k \right)=1\)。
拉格朗日函数求解:
其中,\(\mathbb{I}\left(o_{t}=k \right)\)表示一个示性函数
观测概率矩阵的估计为:
注:这里的\(k\)是索引,为了方便标识,我们将观测集合标识为\(V= \left\{ 1,2,\cdots,M \right\}\),和原始的\(V= \left\{ v_{1},v_{2},\cdots,v_{M} \right\}\)一一对应。
5.2.4 Baum-Welch算法
输入:观测序列 \(O = \left\{ o_{1},o_{2},\cdots,o_{T} \right\}\)
输出:隐马尔可夫模型。
- 初始化参数\(A,B,\Pi\)
- 按照5.2.2求E步
- 按照5.2.3求M步
- 重复第二、三步,知道参数\(A,B,\Pi\)收敛
经过上面的代码验证,我们知道要学习到一个好的模型,我们的观测序列要尽可能长,样本量足够多。
6、隐马尔可夫的预测问题
维特比算法求预测这个比较简单,因为维特比算法太常用了,这里不再赘述。
完!


