transformer
Attention Is All You Need
作者:elfin 参考资料来源:transformer
transformer家族近期炙手可热,不仅霸占了NLP领域的江山,在CV领域也有踢馆CNN的趋势 。那么它有那么牛吗?牛啊牛?在弱人工智能时代,没有永远的神,transformer也是如此,它也有自己擅长、不擅长的数据分布。
transformer在CV中井喷式发展,最近几个月对新技术的梳理、测试,发现像Swin根本不能超越CNN性能,其精度是非常接近CNN系列的SOTA,但是计算速度却裂开了。特别是 GPU算力受限的情况下,你就明白这训练速率让整个人生都卡顿的感觉。最近清华发表了一篇Autoformer,结构设计上非常像NLP任务,但是这个实际上并不能说其超越了transformer结构,因为它的数据分布适应域比较窄,若在一般数据据分布下,其性能一定会退化。当然也有惊喜,新鲜出炉的VOLO为transformer找回了场子 。通过对结构的巧妙设计,在技术上对计算速率进行了处理,在CV领域,作者声称第一次超越了CNN结构 。对此,我目前还没有做任何尝试,但是比较相信,论文结果在一般数据上的良好迁移性。
既然,那么多模型,都子子孙孙无穷尽了,为什么还要回到模开始的地方,研究transformer呢?如果你只是使用别人的工程项目,甚至没有看过此论文,那么你很难对这些理论进行深刻理解;transformer总是让人感觉很高级的样子,我希望让它看起来一点也不高级,用最原始的东西阐述一些“高大”的概念。
下面我们来读论文……
摘要
主要的序列转换模型是基于复杂的递归或卷积神经网络,包括编码器和解码器。性能最好的模型还通过注意机制连接编码器和解码器。我们提出了一个新的简单的网络结构:Transformer,完全基于注意机制,避免了递归和卷积。在两个机器翻译任务上的实验表明,这些模型具有更高的并行性和更少的训练时间。我们的模型在WMT 2014英语到德语的翻译任务中达到28.4 BLEU,比现有的最佳结果(包括聚合模型)提高了2 BLEU以上。在WMT 2014英语-法语翻译任务中,我们的模型在8个GPU上训练3.5天后建立了新的单模型最新BLEU分数41.8,这是文献中最佳模型培训成本的一小部分。通过将Transformer成功地应用于大规模和有限训练数据下的英语选区分析,证明了Transformer具有良好的泛化能力。
1、介绍
递归神经网络,特别是长-短期记忆[13]和门限递归[7]神经网络,已经被确定为序列建模和转换问题(如语言建模和机器翻译)的最新方法[35,2,5]。自那以后,许多努力继续推动提升循环语言模型和编解码器架构的性能[38,24,15]。
递归模型通常沿着输入和输出序列的符号位置进行因子计算。将位置与计算时间步长对齐,它们生成一系列隐藏状态\(h_{t}\),\(h_{t}\)作为先前隐藏状态\(h_{t-1}\)和位置\(t\)的输入的函数。这种固有的顺序性排除了训练示例中的并行化,这在较长的序列长度下变得至关重要,因为内存限制限制了跨示例的批处理。最近的工作通过因子分解技巧[21]和条件计算[32]在计算效率方面取得了显著的改进,同时也提高了后者的模型性能。然而,顺序计算的基本限制仍然存在。
在这项工作中,我们提出了Transformer,一种避免递归出现的模型架构,而完全依赖于一种注意机制来绘制输入和输出之间的全局依赖关系。Transformer允许更明显的并行化,并可以在机器翻译上达到SOTA状态,且在8个P100GPU只要12小时训练时间。
2、背景介绍
为了减少序列计算,也形成了扩展神经GPU〔16〕、ByteNet〔18〕和VusS2S〔9〕的基础,所有这些都使用卷积神经网络作为基本构建块,并行计算所有输入和输出位置的隐藏表示。在这些模型中,将两个任意输入或输出位置的信号关联起来所需的操作数随着位置之间的距离而增长,convs2是线性的,ByteNet是对数的。这使得学习远距离位置之间的依赖关系变得更加困难[12]。在Transformer中,这被减少到一个恒定的操作数,尽管由于平均注意加权位置而降低了有效分辨率,我们用多头部注意抵消了这种影响,如第3.2节所述。
自我注意,有时被称为内部注意,是一种注意力机制,将单个序列的不同位置联系起来,以计算序列的表示形式。自我注意在阅读理解、抽象总结、语篇蕴涵和学习任务无关的句子表征等任务中得到了成功的应用[4,27,28,22]。
端到端记忆网络是基于一种循环注意机制而不是序列对齐的递归,并且在简单的语言问答和语言建模任务中表现良好[34]。
然而,据我们所知,Transformer是第一个完全依靠自我注意来计算其输入和输出的表示,而不使用序列对齐的RNN或卷积的转导模型。在下面的章节中,我们将描述Transformer,激发自我关注,并讨论其相对于[17,18]和[9]等模型的优势。
3、模型架构
大多数竞赛中的模型都有编码解码器结构[5,2,35]。这里,编码器将符号表示\(\left( x_{1}, \cdots ,x_{n} \right)\)的输入序列映射到连续表示\(z = \left( z_{1}, \cdots ,z_{n} \right)\)的序列。给定\(z\),解码器然后一次生成一个元素的符号,得到输出序列\(\left( y_{1}, \cdots ,y_{m} \right)\)。在每一步中,模型都是自回归的[10],在生成下一步时,使用先前生成的符号作为额外的输入。
Transformer遵循这个整体架构,使用堆叠的自我关注和逐点式,编码器和解码器的完全连接层,分别如图1的左半部分和右半部分所示。
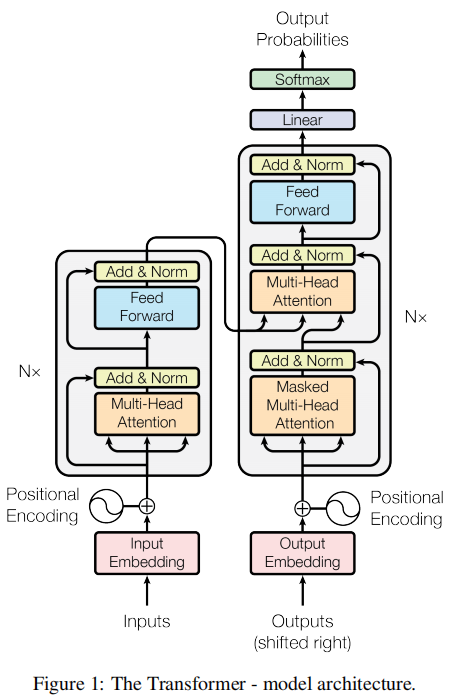
上面这个鬼东西,一看就让人脑壳痛,花里胡哨的……下面我们就看图说话:
上图左边的是编码器:
- 最下面的小粉红是输入,可以理解为对世界万物的数字化抽象对象,简单的说就是词向量;
- 往上走是一个加号,它是与位置编码相加;
- 朝着箭头的方向来到一个灰色的框,注意左边有个\(\text{N}\times\)的符号,表示这样的layer有\(\text{N}\)个;
- 灰色框的 第一个残差连接块,橙色框明确告诉我们它是多头注意力。这就像哪吒,平时跟你说话一个头就好了,要打你的时候就整出三个头。头多了就可以实现数据并行,有利于提升资源占用,提高效率。然后就是残差连接再接layer Norm,可以理解为干完架要打扫一下战场,shortcut就负责给重建提供指导,告诉模型这个团要10名狙击手,别整个低配就来了;MHA分支就是干架的那批人,打赢了就限制一下,别太骄傲,干不过就补充一下。LN就负责给每个人戒骄戒躁,使数据元素整齐划一。
- 而蓝色的块是Feed Forward,一般就是 MLP,主要就是将特征进行融合提取更高级的语义。
- 经过叠加,最后形成输入的编码 ,此时,编码是高维空间中的一个 点,它表示了输入的所有信息。如果信息是完备的,那么我们可以根据这个点得到我们想要的信息。
上图右边的是解码器:
下面是关于上面出现的一些名称说明……
3.1 编码器和解码器堆栈
编码器:编码器由N=6个相同层组成。每层有两个子层。第一层是一种多头自我注意机制,第二种是一种简单的逐点全连接前馈网络。我们在两个子层的每一个子层周围使用残差连接[11],然后使用LN(Layer Normalization)[1]。也就是说,每个子层的输出是\(\text{LayerNorm}\left( x + \text{Sublayer} \left( x \right) \right)\)。为了方便这些残差连接,模型中的所有子层以及嵌入层都会生成维数为\(d_{model}=512\)的输出。
解码器:解码器也由N=6个相同层的堆叠组成。除了每个编码器层中的两个子层之外,解码器还插入第三个子层,该子层对编码器模块的输出执行多头注意力。与编码器类似,我们在每个子层周围使用剩余连接,然后进行LN。我们还修改了解码器堆栈中的自我注意子层,以防止位置涉及后续位置。这种掩蔽与输出嵌入被一个位置偏移的事实相结合,确保位置\(i\)的预测只能依赖于位置小于\(i\)的已知输出。
3.2 Attention
注意函数可以描述为将查询和一组键值对映射到输出,其中查询\(q\)、键\(k\)、值\(v\)和输出都是向量。输出由值和值元素的权值相乘得到,权值是由查询与键相乘得到。如图所示:

3.2.1 点乘缩放注意力
首先我们提出一个问题,为啥要缩放?是不是感觉好像能理解又说不出个所以然!那么你可以参考:https://blog.csdn.net/qq_37430422/article/details/105042303
对应上图的左边,即为点乘缩放注意力机制。计算公式为:
这个公式很简单,作者会有各种理论解释,简单来说就是:
- 我要从一堆信息中得到这层的特征工程挖掘结果;
- 现在我挖了个\(V\)出来,想了一下,这个值矩阵能代表序列信息吗?
- 现在我又想挖个权值向量,对结果加权输出;
- 对于权值的获取总是要满足一些规则的,这里我们挖了一个查询\(Q\)与键\(K\)使用点乘、缩放得到权值
3.2.2 多头注意力机制
如图二所示,我们将\(Q,K,V\)分成\(h\)份,分别执行点乘缩放操作,得到各自的输出,最后再合并。这样做有啥子好处?首先假设之前的向量维度是\(d_{k}\),我们现在每个头的向量维度是\(\frac{d_{k}}{h}\),那这样向量之间的乘法操作我们的多头模型只有原来的\(\frac{1}{h}\)。关键的点在于这\(h\)个头我们可以并行计算,计算量的减少也会直观体现在计算速度上。
多头注意力的计算为:
其中的参数矩阵为:
- \(W_{i}^{Q} \in \mathbb{R}^{d_{model}\times d_{k}}\) , \(W_{i}^{K} \in \mathbb{R}^{d_{model}\times d_{k}}\) , \(W_{i}^{V} \in \mathbb{R}^{d_{model}\times d_{v}}\) ;
- \(W^{O} \in \mathbb{R}^{hd_{v} \times d_{model}}\)
transformer里面设置了8个头,\(d_{k}=d_{v}=d_{model} / h=64\)。由于每个头部的维数减小,总的计算量与全维单头部注意力的计算量相似。
\(h\)个头实际将每个头的计算量相加就和单头计算量一样,后面的计算量几乎可以忽略。
3.2.3 在Transformer中应用注意力机制
在Transformer中以如下三种不同的方式使用多头注意力:
-
在“编码器-解码器注意力”层中,查询来自前一个解码器层,而存储的键和值来自编码器的输出。这使得解码器中的每个位置都可以参与输入序列中的所有位置。这模仿了典型的编码器-解码器在序列到序列模型中的注意机制,如[38,2,9]。
第一种实现我们可以在架构中直接找到:

这种实现只是在编码器向解码器过渡的层。
-
编码器包含自我注意层。在self-attention层中,所有的键、值和查询都来自同一个地方,在本例中是编码器中前一层的输出。编码器中的每个位置都可以关注编码器前一层中的所有位置。
-
类似地,解码器中的自我关注层允许解码器中的每个位置关注到解码器中直到并且包括该位置的所有位置。我们需要防止解码器中的信息流向左流动,以保持自回归特性。我们通过Mask输出: softmax输入中与非法连接相对应的所有值(设置为\(-\infty\))。见图2。
这部分就是:
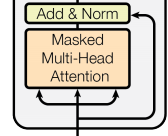
3.3 位置感知前馈网络
除了注意子层之外,我们的编码器和解码器中的每一层都包含一个全连接前馈网络,该网络分别相同地应用于每个位置。这包括两个线性变换,中间有一个ReLU激活。
一般在代码中你会看到一个MLP层,就是位置感知前馈网络的实现。
虽然线性变换在不同的位置上是相同的,但它们在层与层之间使用不同的参数。另一种描述方法是两个核大小为1的卷积。输入和输出的维数为\(d_{model}\)=512,内层的维数为\(d_{ff}=2048\)。
3.4 Embeddings and Softmax
与其他序列转换模型类似,我们使用学习的编码器将输入tokens和输出tokens转换为维度\(d_{model}\)的向量。我们还使用线性变换和softmax函数将解码器输出转换为预测的下一个token概率。在我们的模型中,我们在两个嵌入层和预softmax线性变换之间共享相同的权重矩阵,类似于[30]。在编码层中,我们将这些权重乘以\(\sqrt{d_{model}}\)。
3.5 位置编码
由于我们的模型不包含递归和卷积,为了使模型能够利用序列的顺序,我们必须注入一些关于符号在序列中的相对或绝对位置的信息。为此,我们将“位置编码”添加到编码器和解码器堆栈底部的输入嵌入中。位置编码与嵌入具有相同的维度\(d_{model}\),因此可以将两者相加。有许多位置编码可以选择,如学习的和固定的[9]。
在这项工作中,我们使用不同频率的正弦和余弦函数:
其中\(pos\)是位置,\(i\)是向量维度。也就是说,位置编码的每个维度对应于一个正弦曲线。波长呈几何级数从\(2π\)到\(10000·2π\)。我们之所以选择这个函数,是因为我们假设它可以让模型很容易地通过相对位置来学习,因为对于任何固定的偏移量\(k\),\(PE_{pos+k}\)可以表示为\(PE_{pos}\)的线性函数。
注:为啥子使用正余弦函数进行位置编码,我想上面的解释大概率对于大部分看这篇文章的小菜鸟都不明白,那么建议到苏剑林的博客下一探究竟。
我们还尝试使用学习到的位置嵌入[9],发现这两个版本产生了几乎相同的结果(见表3第(E)行)。我们选择正弦版本,因为它可能允许模型外推序列长度比训练中遇到的更长。
完!


