YOLOR: 基于多任务的统一网络
You Only Learn One Representation: 对于多任务的统一网络
论文地址:https://arxiv.org/abs/2105.04206
项目地址:https://github.com/WongKinYiu/yolor
摘要
人们通过视觉、听觉、触觉以及过去的经验来“理解”世界。人类的经验可以通过正常的学习(我们称之为显性知识)或潜意识(我们称之为隐性知识)来学习。这些通过正常学习或潜意识学习到的经验将被编码并储存在大脑中。利用这些丰富的经验作为一个巨大的数据库,人类可以有效地处理数据,即使它们是事先看不见的。本文提出了一个统一网络,将内隐知识和外显知识编码在一起,就像人脑可以从正常学习和潜意识学习中学习知识一样。统一网络可以生成一个统一的表示,同时服务于各种任务。我们可以在卷积神经网络中执行核空间对齐、预测精化和多任务学习。结果表明,将内隐知识引入到神经网络中,有利于所有任务的执行。我们进一步分析了从所提出的统一网络中学习到的隐式表示,它显示出很强的捕捉不同任务物理意义的能力。
1、介绍
如图1所示,人类可以从不同的角度分析同一段数据。然而,经过训练的卷积神经网络(CNN)模型通常只能实现一个目标。一般来说,从训练过的CNN中提取出来的特征通常对其他类型的问题适应性较差。造成上述问题的主要原因是我们只从神经元中提取特征,而没有利用CNN中丰富的内隐知识。在真实人脑运行时,上述隐性知识可以有效地辅助大脑完成各种任务。

隐性知识是指在潜意识中学习到的知识。然而,对于内隐学习如何运作以及如何获得隐性知识,目前还没有一个系统的定义。在神经网络的一般定义中,从浅层获得的特征通常称为显式知识,从深层获得的特征称为隐式知识。本文将与观察直接对应的知识称为显性知识。对于模型中隐含的与观察无关的知识,我们称之为隐性知识。
我们提出了一个统一的网络来整合隐式知识和显式知识,使学习模型包含一个通用的表示,这个通用的表示使得子表示适合于各种任务。图2(c)说明了拟议的统一网络体系结构。
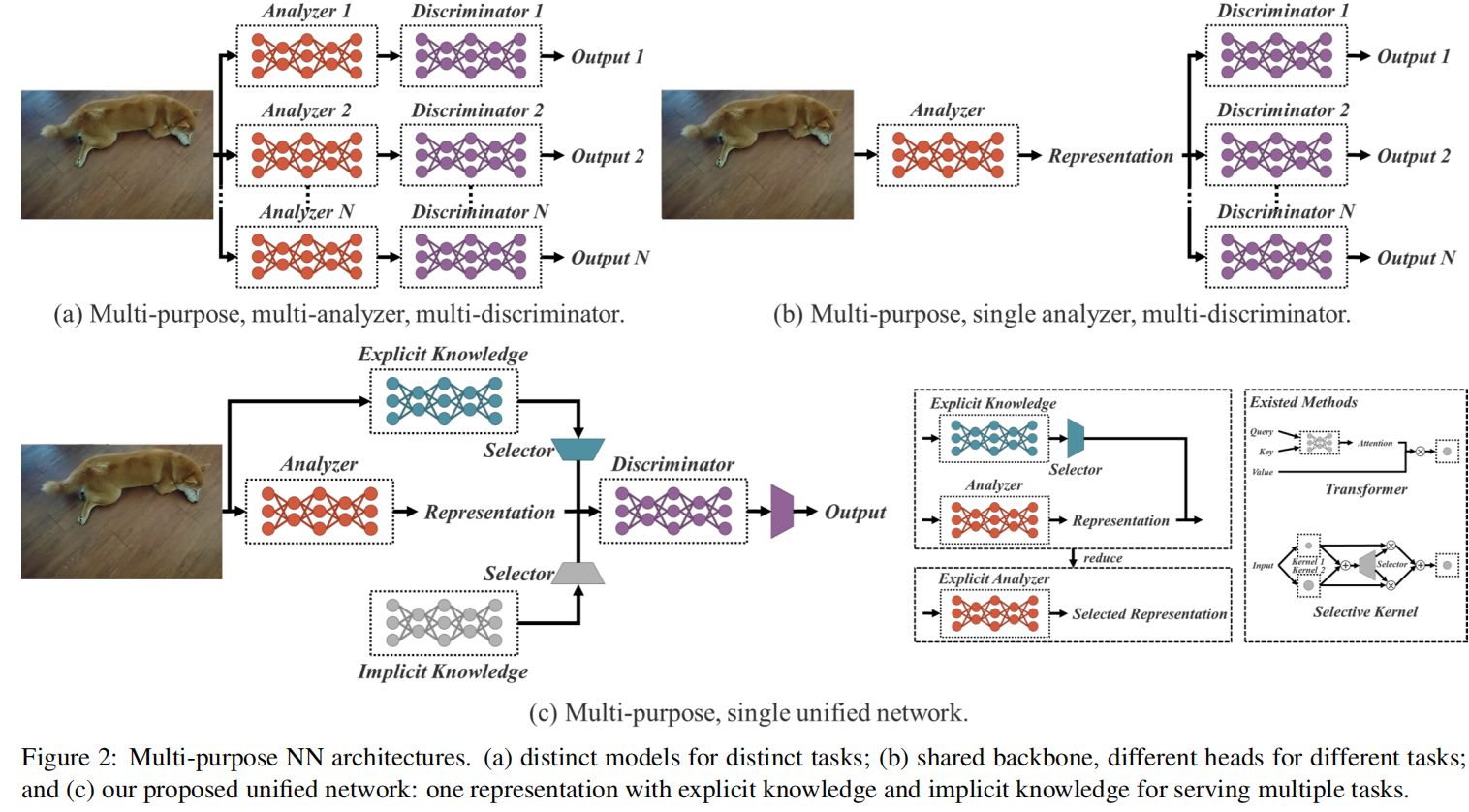
构建上述统一网络的方法是将压缩感知和深度学习结合起来,主要的理论基础可以在我们之前的工作中找到[16,17,18]。在[16]中,我们证明了用扩展字典重构残差的有效性。在[17,18]中,我们使用稀疏编码来重建CNN的特征图,使其更具鲁棒性。这项工作的贡献总结如下:
- 我们提出了一个能够完成各种任务的统一网络,它通过整合隐式知识和显式知识来学习一个通用表示,通过这个通用表示可以完成各种任务。所提出的网络有效地提高了模型的性能,只需很小的额外成本(不到参数和计算量的1万)。
- 将kernel空间对齐、预测修正和多任务学习引入到内隐知识学习过程中,验证了它们的有效性。
- 分别讨论了利用向量、神经网络、矩阵分解等工具对隐含知识进行建模的方法,并验证了其有效性。
- 我们证实了所提出的内隐表征学习方法能够准确地对应于特定的物理特征,并且我们还以视觉的方式呈现了它。我们还证实,如果算子符合目标的物理意义,它可以用来整合内隐知识和外显知识,并会产生乘法效应。
- 结合最新的方法,我们提出的统一网络在目标检测方面达到了与Scaled-YOLOv4-P7[15]相当的精度,推理速度提高了88%。
2、相关工作
我们对这一研究课题的相关文献进行了综述。本文的文献综述主要分为三个方面:
-
外显深度学习:它将涵盖一些基于输入数据自动调整或选择特征的方法;
-
内隐深度学习:它将涵盖内隐深度知识学习和内隐微分导数的相关文献;
-
知识建模:列举了几种可以用来整合内隐知识和外显知识的方法。
2.1 外显深度学习
外显深度学习可以通过以下方式进行。其中Transformer[14,5,20]是一种方式,它主要使用查询、键或值来获得自我关注。非局域网络[21,4,24]是另一种获取注意力的方式,它主要在时间和空间上提取成对的注意力。另一种常用的显式深度学习方法[7,25]是通过输入数据自动选择合适的内核。
2.2 内隐深度学习
属于内隐深度学习范畴的方法主要有内隐神经表征[11]和深度均衡模型[2,3,19]。前者主要是获得离散输入的参数化连续映射表示,以执行不同的任务;后者是将隐式学习转化为残差形式的神经网络,并对其进行平衡点计算。
2.3 知识模型
对于属于知识建模范畴的方法,主要包括稀疏表示[1,23]和记忆网络[22,12]。前者使用样例、预定义过完备或学习词典进行建模,后者则依赖于多种嵌入形式的结合来形成内存,使内存能够动态地添加或更改。
3、如何让内隐知识工作?
本研究的主要目的是建立一个能够有效训练内隐知识的统一网络,因此在后续的研究中,我们首先将重点放在如何训练内隐知识和快速推理上。由于隐式表示\(z_{i}\)与观测无关,我们可以把它看作一组常数张量\(Z=\{z_{1},z_{2},\cdots,z_{k}\}\)。在本节中,我们将介绍作为常量张量的内隐知识如何应用于各种任务。
3.1 多维空间降维
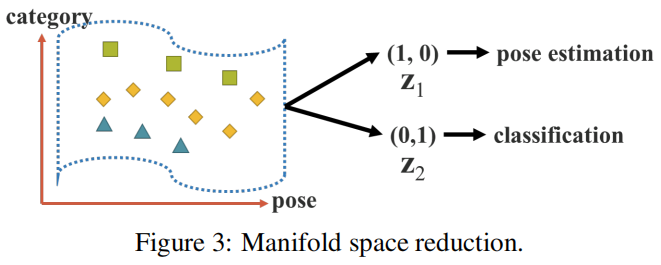
我们认为,一个好的表征应该能够在它所属的多维空间中找到一个合适的投影,并有助于后续目标任务的顺利完成。例如,如图3所示,如果目标类别可以通过投影空间中的超平面成功分类,那将是最好的结果。在上面的例子中,我们可以利用投影向量的内积和隐式表示来达到降低流形空间维数的目的,有效地完成各种任务。
3.2 内核空间对齐
在多任务和多头神经网络中,核空间失调是一个常见的问题,图4(a)举例说明了多任务和多头神经网络中的核空间失调。为了解决这个问题,我们可以对输出特征和隐式表示进行加法和乘法,这样就可以对核空间进行平移、旋转和缩放,以对齐神经网络的每个输出核空间,如图4(b)所示。上述操作模式可广泛应用于不同领域,如特征金字塔网络(FPN)[8]中大对象与小对象的特征对齐、利用知识提炼来集成大模型与小模型、零例域转移的变换等问题。

3.3 更多的功能
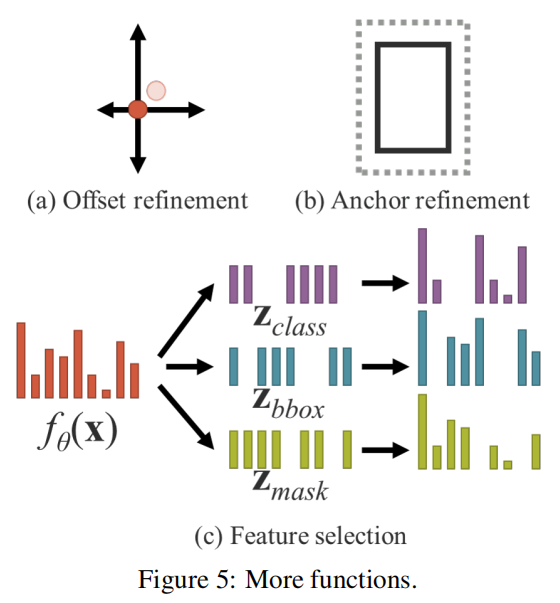
除了可以应用于不同任务的功能外,内隐知识还可以扩展为更多的功能。如图5所示,通过引入加法,可以使神经网络预测中心坐标的偏移量。还可以引入乘法来自动搜索锚点的超参数集,这是基于anchor的目标检测经常需要的。此外,点乘法和串联可分别用于执行多任务特征选择和为后续计算设置前提条件。
4、统一网络的内隐知识
在本节中,我们将比较传统网络和提出的统一网络的目标函数,并解释为什么引入隐含知识对训练多用途网络很重要。同时,我们还将详细阐述本文提出的方法。
4.1 内隐知识的公式
4.1.1 卷积网络
对于卷积网络的目标函数,如下:
卷积网络训练,即最小化误差\(\varepsilon\),使卷积网络尽可能贴近真实数据 \(y\)。如图6(a)所示,我们需要对同一标注有不同的样本,以获取数据的丰度。换句话说,我们期望得到的解空间仅对当前任务\(t_{i}\)是有区别的,并且对各种潜在任务中除\(t_{i}\)以外的任务是不变的,其中\(T=\left \{ t_{1},\cdots ,t_{n} \right \}\)。
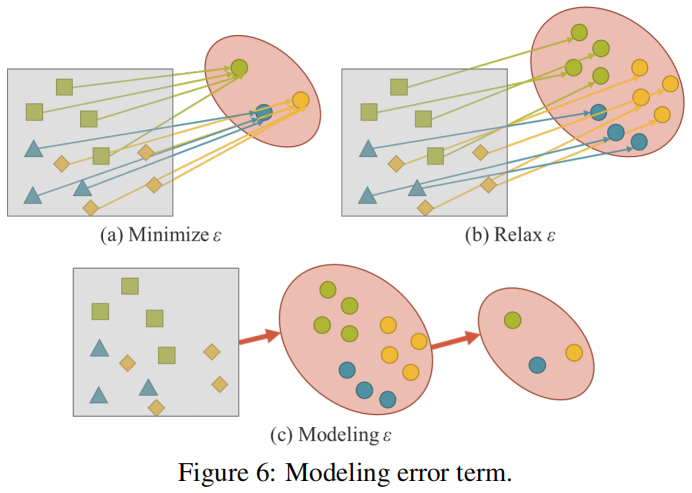
对于一般用途的神经网络,我们希望所得到的表示能服务于\(T\)。因此,我们需要放松\(\varepsilon\),以便在流形空间上同时找到每个任务的解,如图6(b)所示。然而,上述要求使得我们不可能用简单的数学方法,如一个one-hot向量的最大值或欧氏距离的阈值来求解\(t_{i}\)。为了解决这个问题,我们必须对错误项\(\varepsilon\)进行建模,以便为不同的任务找到解决方案,如图6(c)所示。
4.1.2 统一网络
为了训练所提出的统一网络,我们将显式知识和隐式知识结合起来对误差项进行建模,然后用它来指导多用途网络的训练过程。相应的训练公式如下:
其中\(\epsilon_{ex}\)和\(\epsilon_{im}\)是分别对观测值\(\textbf{X}\)和潜在代码\(\textbf{Z}\)的显式误差和隐式误差进行建模的运算。\(g_{\phi}\)这里是一个特定于任务的操作,用于从显性知识和隐性知识中组合或选择信息。
已有的将显式知识整合到\(f_{θ}\)的方法,可以将(2)改写为(3)。
其中\(\star\)表示了\(f\)和\(g\)之间的可能操作。在这项工作中,将使用第3节中介绍的运算符,即加法、乘法和级联。
如果我们把误差项的推导过程扩展到处理多个任务,我们可以得到如下公式:
其中,\(\textbf{Z}=\left \{ \textbf{z}_{1},\textbf{z}_{2},\cdots ,\textbf{z}_{T} \right \}\)是不同任务的隐式代码,\(\Phi\)是用于从\(\textbf{Z}\)生成内隐知识表示的参数,\(\Psi\)用于从显式表示和隐式表示的不同组合中计算最终输出参数。
对于不同的任务 ,我们可以使用下面的公式获得预测:
对于所有的任务我们都从一个统一表示\(f_{\theta }\left ( \textbf{x} \right )\),完成特定任务的隐式表示\(g_{\Phi }\left ( \textbf{z} \right )\)开始,最后用任务识别器\(d_{\Psi }\)完成不同的任务。
4.2 内隐知识建模
我们提出的隐性知识可以通过以下方式建模:
4.2.1 Vector / Matrix / Tensor
向量\(\textbf{z}\)直接作为内隐知识的先验,直接作为隐式表示。此时,必须假设每个维度彼此独立。
4.2.2 神经网络
利用向量z作为隐式知识的先验,然后利用权矩阵W进行线性组合或非线性化,成为隐式表示。此时,必须假设每个维度相互依赖。我们也可以使用更复杂的神经网络来生成隐式表示。或者用马尔可夫链来模拟不同任务间隐式表示的相关性。
4.2.3 矩阵分解
利用多个向量作为隐式知识的先验,这些隐式先验基\(\textbf{Z}\)和系数\(\textbf{c}\)构成隐式表示。我们还可以进一步对\(\textbf{c}\)进行稀疏约束,并将其转化为稀疏表示形式。此外,我们还可以对\(\textbf{Z}\)和\(\textbf{c}\)施加非负约束,将它们转化为非负矩阵分解(NMF)形式。
4.3 训练
假设我们的模型在开始时没有任何先验的隐式知识,也就是说,它不会对\(f_{\theta}\left( \textbf{x} \right)\)的显式表示产生任何影响。当操作\(\star \in \left\{ addition,\ concatenation \right\}\),我们设置内隐知识服从\(\textbf{z} \sim N\left( 0, \ \sigma \right)\);当操作是乘法时,\(\textbf{z} \sim N\left( 1, \ \sigma \right)\)。这里的标准差是一个非常接近零的数。对于\(\textbf{z}\)和\(\phi\),在训练过程中均采用反向传播算法进行训练。
4.4 推理
由于隐式知识与观测值\(\textbf{x}\)无关,因此无论隐式模型\(g_{\phi}\)有多复杂,都可以在推理阶段开始前将其化为一组常数张量。换句话说,隐式信息的形成对算法的计算复杂度几乎没有影响。另外,当上面的运算是乘法时,如果后面的层是一个卷积层,那么我们用下面的(9)来积分。当遇到加法运算符时,如果前一层是卷积层并且没有激活函数,则使用下面所示的(10)进行积分。
其中,\({W}'_{l}=W_{l} g_{\phi} \left( \textbf{z} \right)\)。
其中,\({b}'_{l}=b_{l} + g_{\phi} \left( \textbf{z} \right)\)
完!


