Autoformer
Autoformer:用于长期序列预测的自相关分解Transformer
作者:elfin 参考资料来源:Autoformer
摘要
时间的长依赖预测是极端天气预警和长期能源消耗规划等实际应用的关键需求。本文研究时间序列的长期预测问题。先前的tranformer模型采用各种自我注意机制来发现长期依赖关系。然而,长期依赖复杂的时间模式阻碍了模型找到可靠的依赖关系。同时,为了提高长期效率,tranformer必须采用点式自关注的稀疏形式,造成了信息利用的瓶颈。针对这些挑战,我们提出了一种具有自相关机制的新型分解结构Autoformer。我们超越了级数分解的预处理约定,将其更新为深度模型的基本内部块。这种设计使Autoformer具有复杂时间序列的渐进分解能力。进一步,受随机过程理论的启发,设计了基于序列周期性的自相关机制,在子序列层次上进行相关性发现和表示聚合。自相关在效率和准确性上都优于自我注意。在长期预测中,Autoformer的准确率达到了最先进的水平,在六个基准上相对提高了38%,涵盖了五个实际应用:能源、交通、经济、天气和疾病。
1、背景介绍
时间序列预测在能源消耗、交通与经济规划、天气与疾病传播预测等方面有着广泛的应用。在这些实际应用中,一个迫切的需求是将预测时间延长到遥远的将来。因此,本文研究了时间序列的长期预测问题,其特点是预测序列的长度很大,可以是输入序列长度的几倍。最近的深度预测模型[42,17,20,36,28,19]已经取得了很大的进展,特别是基于tranformer的模型。得益于自我注意机制,Transformers在为序列数据建模长期依赖性方面获得了巨大优势,这使得更强大的大模型成为可能[7,11]。
然而,在长期的背景下,预测任务是极具挑战性的。首先,直接从长期时间序列中发现时间依赖关系是不可靠的,因为时间依赖关系会被复杂的时间模式所掩盖。其次,由于序列长度的二次复杂性,具有自我注意机制的正则变换在长期预测中的计算上是禁止的。以前基于tranformer的预测模型[42,17,20]主要关注于提高对稀疏版本的自我关注。虽然性能显著提高,但这些模型仍然使用逐点表示聚合。因此,在提高效率的过程中,它们会因为稀疏的逐点连接而牺牲信息利用率,从而成为时间序列长期预测的瓶颈。
为了解释复杂的时间模式,我们尝试采用分解的思想,这是时间序列分析的标准方法[1,27]。它可以用来处理复杂的时间序列和提取更可预测的组件。但在预测背景下,由于未来未知,只能作为过去序列的预处理[15]。这种常见用法限制了分解的能力,并且忽略了分解组件之间潜在的未来交互。因此,我们尝试超越分解的预处理使用,并提出一个通用架构,以赋予深度预测模型内在的渐进分解能力。此外,分解可以解开纠缠的时间模式,突出时间序列的固有特性[15]。基于此,我们尝试利用序列的周期性来更新自我注意中的点连接。我们观察到,在同一相位的子序列中,周期之间往往呈现相似的时间过程。因此,我们尝试建立一个基于序列周期性的过程相似性的序列级连接。
基于上述动机,我们超越了tranformer,提出了一种新的用于长期时间序列预测的Autoformer。Autoformer仍然遵循残差和编解码器结构,但将Transformer更新为分解预测结构。通过嵌入我们提出的分解块作为内算子,Autoformer可以从预测的隐藏变量中逐步分离出长期趋势信息。这种设计允许我们的模型在预测过程中交替分解和细化中间结果。受随机过程理论[8,24]的启发,Autoformer引入了一种自相关机制来代替自我注意,它根据序列的周期性发现子序列的相似性,并从底层周期中聚集相似的子序列。该机制实现了长度为\(L\)的序列的\(O(LlogL)\)复杂度,通过将点表示聚合扩展到子序列级,突破了信息利用的瓶颈。Autoformer在六个基准上实现了最先进的精度。主要贡献如下:
- 为了解决长期依赖复杂的时间模式,我们将Autoformer作为一种分解结构,并设计内部分解块来赋予深度预测模型内在的渐进分解能力。
- 我们提出了一种在序列级进行依赖项发现和信息聚合的Auto-Correlation机制。我们的机制超越了以往的自我关注家族,可以同时提高计算效率和信息利用率。
- Autoformer在六个基准的长期设定下实现了38%的相对改善,涵盖了五个实际应用:能源、交通、经济、天气和疾病。
2、相关工作
2.1 时间序列预测模型
由于时间序列预测的重要性,各种模型得到了很好的发展。许多时间序列预测方法都是从经典工具开始的[33,9]。ARIMA[6,4]通过差分将非平稳过程转化为平稳过程来解决预测问题。对序列预测也引入了滤波方法[18,10]。此外,使用递归神经网络(RNNs)模型对时间序列的时间依赖性进行建模[37,26,41,22]。DeepAR[28]结合了自回归方法和RNNs来模拟未来序列的概率分布。LSTNet[19]引入了卷积神经网络(CNNs)和循环跳跃连接来捕捉短期和长期的时间模式。基于注意的RNN[40,31,32]引入了时间注意来探索预测的长期依赖性。同时,许多基于时间卷积网络(TCN)[35,5,3,29,30]的工作试图用因果卷积来建模时间因果关系。这些深度预测模型主要集中在通过循环连接、时间注意或因果卷积进行时间关系建模。
最近,基于自我注意机制的tranformer[36,39]在自然语言处理[11,7]、音频处理[14]甚至计算机视觉[12,21]等后续数据中显示出巨大的威力。然而,由于序列在记忆和时间上有长度为\(L\)的二次复杂性,将自我注意应用于长期时间序列预测在计算上是禁止的。LogTrans[20]将局部卷积引入到Transformer中,提出了LogSparse注意选择指数增长区间后的时间步长,将复杂度降低到\(O(L(logL)^{2})\)。Reformer[17]提出了局部敏感哈希(LSH)注意,并将复杂性降低到\(O(Llog L)\)。Informer[42]利用KL散度扩展了Transformer,并实现了\(O(Llog L)\)复杂性。请注意,这些方法基于vanilla Transformer,并尝试将自我注意机制改进为稀疏版本,该版本仍然遵循逐点依赖和聚合。在本文中,我们提出的Autoformer机制是基于时间序列固有的周期性,可以提供串行连接。
2.2 时间序列分解
作为时间序列分析中的一种标准方法,时间序列分解[1,27]将时间序列分解为几个组成部分,每个组成部分代表更可预测的基本模式类别之一。它主要用于探索随时间推移的历史变化。对于预测任务,在预测未来序列之前,通常采用分解作为历史序列的预处理[15],如Prophet[34]等[2]。然而,这样的预处理受到了历史序列的简单分解效应的限制,忽略了序列内在模式之间的层次性交互作用。本文从一个新的递进维度出发,引入了分解思想。我们的Autoformer将分解作为深层模型的内部块,在整个预测过程中逐步分解隐藏的序列。
3、Autoformer
时间序列预测问题是给定过去的长度\(I\)序列,预测未来最可能的长度\(O\)序列,表示为\(Input-I-predict-O\)。长期预测设置是根据短期历史预测长期未来,即\(O>i\)。如上所述,我们强调了长期序列预测的困难:处理复杂的时间模式,打破计算效率和信息利用的瓶颈。为了解决这两个难题,我们将分解作为一个内置块引入深度预测模型,并提出Autoformer作为一个分解体系结构。此外,我们还设计了自相关机制来发现基于周期的依赖关系,并从底层周期聚合相似的子序列。
3.1 结构分解
我们将Transformer[36]更新为一个深度分解架构(图1),包括内部序列分解块、自相关机制以及相应的编码器和解码器。
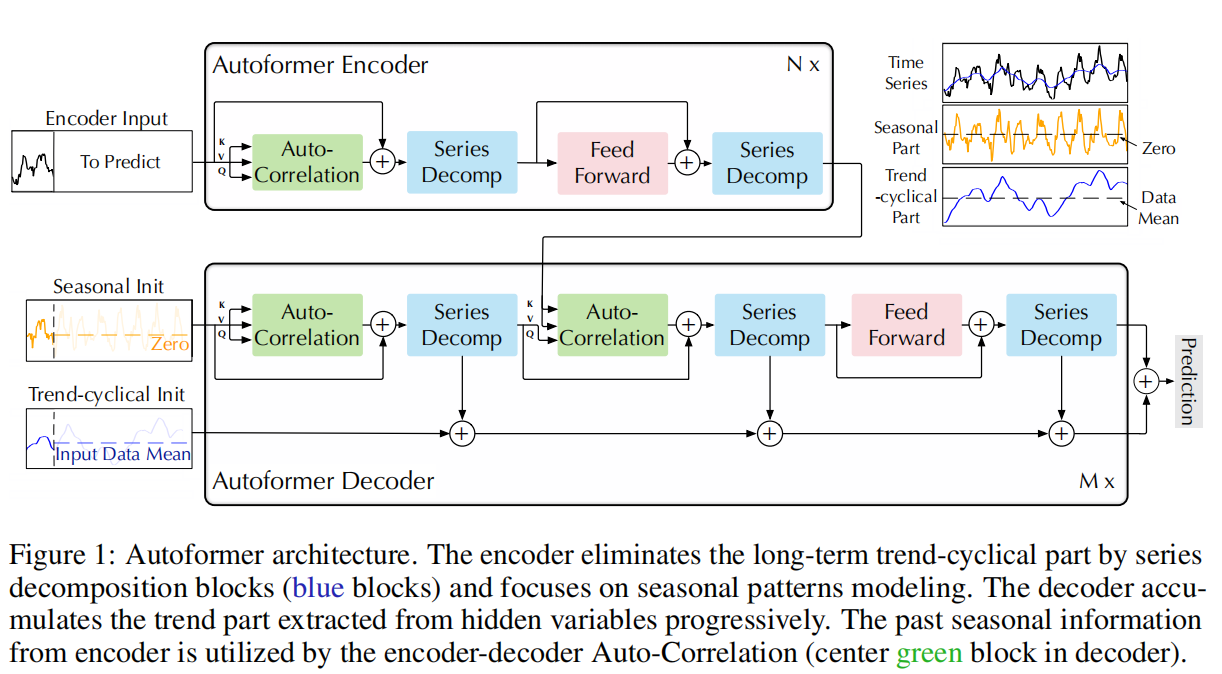
3.1.1 序列分解模块
为了在长期预测环境中学习复杂的时间模式,我们采用了分解的思想[1,27],它可以将序列分为趋势周期和季节部分。这两部分分别反映了序列的长期演变和季节性。然而,直接分解未来序列是不可能的,因为未来是未知的。为了解决这个难题,我们提出了一个序列分解块作为Autoformer的内部操作(图1),它可以逐步从预测的中间隐藏变量中提取长期平稳趋势。具体来说,我们采用移动平均来平滑周期性波动,突出长期趋势。对于长度为\(L\)的输入序列\({\color{Red} X}\in \mathbb{R}^{L\times d}\),处理过程为:
上面的公式分别提取了季节性和周期性趋势。我们使用\(X_{s}, X_{t} = \text{SeriesDecomp}\left( X \right)\)总结上面的处理过程,它在Autoformer中表现为一个 内部block。
3.1.2 模型输入
编码器部分的输入是过去的\(I\)时间步\(X_{en} \in \mathbb{R}^{I \times d}\)。如图一中的编码器所示,输入包括季节性部分\(X_{des} \in \mathbb{R}^{\left( \frac{I}{2} + O \right) \times d}\)和周期性部分\(X_{det} \in \mathbb{R}^{\left( \frac{I}{2} + O \right) \times d}\)。每个初始化由两部分组成:从编码器输入$X_{en} \(的后半部分分解的组件,长度为\)\frac{I}{2}\(以提供最新信息;长度为由标量填充\)O$的占位符。公式表诉如下:
其中公式(3)表示提取$X_{en} \(的季节性和周期性趋势;\)X_{0},X_{Mean}\in\mathbb{R}^{O\times d}\(分别表示\)X_{en} $的零、均值填充。
3.1.3 编码器
如图一所示,编码器主要聚焦于季节性建模。输出主要包含了过去的季节性信息,帮助解码器细化预测结果。假设我们有N个编码层。对于第\(l\)个编码层的操作我们使用\(X_{en}^{l}=\text{Encoder}\left ( X_{en}^{l-1} \right )\)表示。详细的处理过程为:
其中"_"表示消除趋势部分。每一层的输出\(S_{en, \_}^{l,2}\)作为下一层的输入,第一个编码器的输入是\(X_{en}^{0}=X_{en}\)。\(S_{en, \_}^{l,i},\ i \in \left\{1,2 \right\}\)分别表示第\(l\)个编码器第\(i\)个序列分解模块的季节因素。我们将在下一节详细描述AutoCorrelation,它可以无缝地取代自我注意。
3.1.4 解码器
解码器包含两部分:周期趋势分量的累积结构和季节分量的叠加自相关机制(图1)。每个解码层包含内部自相关块和编码解码器自相关块,分别对预测进行细化和利用过去的季节信息。注意,该模型在解码器期间从中间隐藏变量中提取潜在趋势,允许Autoformer逐步细化趋势预测并消除干扰信息,以便在自相关中基于周期的相关性发现。假设 有M个解码层。解码器的隐状态为\(X_{en}^{N}\),则第\(l\)层解码器所作的处理为\(X_{de}^{l} = \text{Decoder}\left( X_{de}^{l-1},X_{de}^{N}\right)\)。解码器可以表示为如下过程:
其中,\(X_{de}^{l}=S_{de}^{l,3},\ l \in \left\{ 1, \cdots, M\right\}\)表示第\(l\)层 解码器的输出。\(S_{de}^{0} , \Tau_{de}^{0}\)分别使用\(X_{des} , X_{det}\)。\(S_{de}^{l,i} , \Tau_{de}^{l,i}\)分别表示第\(l\)层第\(i\)个序列分解的季节因素、周期性因素块。\(W_{l,i}\)表示\(\Tau_{de}^{l,i}\)的线性投影变换因子适配器。
最终我们可以使用算子 $ W_{s} * X_{de}^{M} + W_{\Tau} * \Tau_{de}^{M}$ 表示整个解码器组件,其中\(W_{s}\)和\(W_{\Tau}\)分别表示季节因素、周期因素的投影因子。
3.2 Auto-Correlation 机制
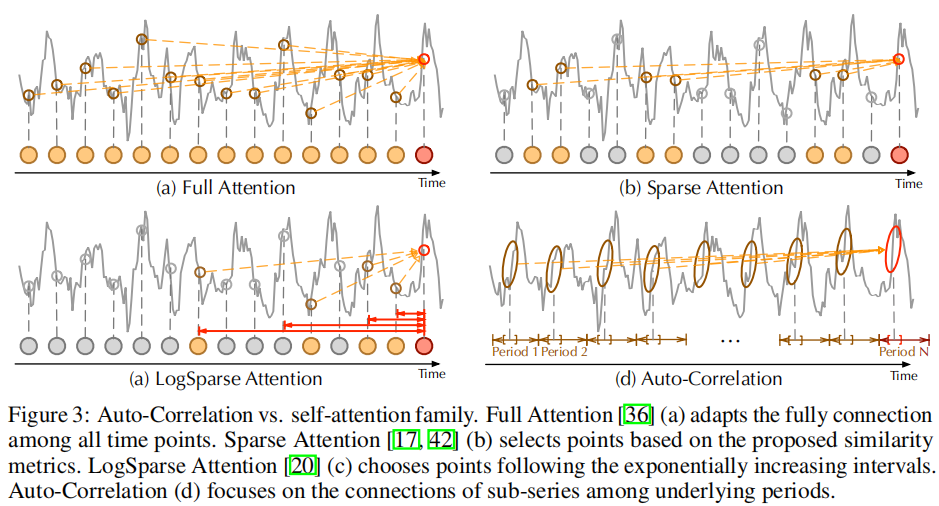
如图2所示,我们提出了具有串行连接的自相关机制,以扩展信息利用率。自相关通过计算序列的自相关来发现基于周期的相关性,并通过时延聚合来聚合相似的子序列。

3.2.1 基于周期的相关性
可以观察到,周期之间相同的相位位置自然提供相似的子过程。受随机过程理论[8,24]的启发,对于一个实际的离散时间过程\(\left\{ X_{t} \right\}\),我们可以通过以下方程得到自相关\(R_{XX}\left ( \tau \right )\):
上面的公式是序列\(\left\{ X_{t} \right\}\)与\(\tau\)阶滞后序列\(\left\{ X_{t-\tau} \right\}\)的时延相关性。这里我们使用\(R\left ( \tau \right )\)表示周期长度为\(\tau\)的非标准置信度评估。如图所示,我们选择了可能的\(k\)个周期长度,进行周期的依赖发现。这里我们会选择最大是\(R\left ( \tau_{k} \right )\)对应的\(\tau_{k}\)。基于周期的依赖关系由上述估计周期导出,并可通过相应的自相关进行加权(选择Top-n个周期,进行加权)。
3.2.2 时延信息聚合
为了实现序列级连接,还需要将相似的子序列信息进行聚合。因此,我们提出了时延聚合模块(图2),它可以基于选定的时延\(τ_{1},···,τ_{k}\)序列。这种操作可以将估计周期的同一相位上的相似子序列对齐,这与自我注意家族中的点积聚合不同。最后,利用\(softmax\)归一化置信度对子序列进行聚合。
对于单头模型,一个长度为\(L\)的序列\(X\),在经过投影后,得到查询\(Q\)、键\(K\)、值\(V\)。因此,我们可以像self-attention一样进行数据处理。Auto-Correlation 机制为:
这里我们对\(Topk\)的设置是采样\(c * logL\)的形式计算(向下取整),\(c\)为超参数。\(R_{Q,K}\)表示\(Q,K\)序列的相关性,\(Roll\left ( X, \tau \right )\)表示将序列\(X\)进行\(\tau\)阶时延操作。对于编码器解码器Auto-Correlation,\(K,V\)是从编码器$X_{en}^{N} \(并resize到\)\left { \frac{I}{2} + O \right }$ 的长度;\(Q\)是用于解码的block。
对于多头模型,隐变量的通道数为\(d_{model}\),假设头的数量为\(h\),第 \(i\)个头的query、key、value为\(Q_{i}, K_{i}, V_{i} \in \mathbb{R}^{L \times \frac{d_{model}}{h}},\ i\in \left\{1,\cdots,h \right\}\)。处理过程为 :
3.2.3 高效的计算
对于基于周期的依赖,这些依赖关系指向底层周期的同一阶段位置的进程,并且本质上是稀疏的。在这里,我们选择最可能的\(τ\)来避免选择相反的相位。所以,公式\(\left ( 13 \right )\rightarrow \left ( 17 \right )\)的计算复杂度为\(O\left(L\ \text{log}L \right)\)。对于自相关计算公式\(\left ( 12 \right )\),给定序列\(\left\{X_{t} \right\}\),自相关序列\(R_{XX}\left ( \tau \right )\)计算可以由基于\(Wiener–Khinchin\)理论的快速傅里叶变换得到:
这里的\(\tau \in \left\{ 1,\cdots,L \right\}\),\(F\)表示快速傅里叶变换,且\(F^{-1}\)表示\(F\)的逆运算,\(F^{*}\)表示\(F\)的共轭,\(S_{XX} \left( f \right)\)表示频域。注意,\({1,\cdots,L}\)中所有滞后的序列自相关可以通过FFT一次计算出来。因此,自相关实现了\(O \left( L \text{log}L \right)\)复杂性。
3.2.4 Auto-Correlation与传统的相关簇之间的比较
与逐点点式的self-attention家族不同,自相关呈现出一系列的联系(图3)。具体地说,对于时间相关性,我们基于周期性找到子序列之间的相关性。相反,self-attention家庭只计算分散点之间的关系。虽然一些self-attentions[20, 42]考虑局部信息,但他们仅利用它来帮助逐点依赖发现。对于信息聚合,我们采用延时块来聚合来自底层周期的相似子序列。相比之下,self-attention则通过点积来聚集所选的点。自相关由于其固有的稀疏性和子序列级的表示聚集性,可以同时提高计算效率和信息利用率。
4、总结
这篇论文的模型设计非常有针对性,数据特点比较明确——数据序列有明显的季节性和周期性。如果序列数据没有这种特性,那么这种设计就暗淡了。整篇论文给人的感觉是创新性不大,如果你是学数学的,你会对作者的所有处理感到非常熟悉。当然作者提出的模型还是有贡献的,传统的技术都简洁优美,作者将其与深度学习技术进行融合,在预测性能上肯定可以有所提升。
完!


