Unfold与fold介绍
Unfold+fold
1、nn.Unfold
nn.Unfold是pytorch实现的一个layer,那么这个layer是干嘛的呢?
torch.nn.Unfold(kernel_size: Union[T, Tuple[T, ...]],
dilation: Union[T, Tuple[T, ...]] = 1,
padding: Union[T, Tuple[T, ...]] = 0,
stride: Union[T, Tuple[T, ...]] = 1)
这里有四个参数,与我们熟知的卷积操作很相似,那么与卷积有什么区别?
实际上nn.Unfold就是卷积操作的第一步。
对于输入特征图shape=[N,C,H,W],我们的Conv2d是怎么工作的?
-
第一步,padding特征图;
-
第二步,过滤器窗口对应的特征图区域,平铺这些元素;
-
第三步,根据步长滑动窗口,并进行第二步的计算;
此时我们得到的特征图\(shape=\left[ N, C \times k \times k, \frac{H}{stride} \times \frac{W}{stride} \right]\)
上面的shape这里给的是一般情况的特例,实际我们表示为:
\(shape=(N, C \times \prod(\text{kernel_size}), L)\),其中\(L\)的计算为:
\[L = \prod_d \left\lfloor\frac{\text{spatial_size}[d] + 2 \times \text{padding}[d] % - \text{dilation}[d] \times (\text{kernel_size}[d] - 1) - 1}{\text{stride}[d]} + 1\right\rfloor \]以上三步实际就是为乘法做准备!
-
第四步,将卷积核与 Unfold 之后的对象相乘;
-
第五步:[nn.Fold]
nn.Unfold就是将输入的特征图“reshape”到卷积乘法所需要的形状,只是很多元素在特征图中是重叠出现的,所以叫unfold,即我们要先平铺。
2、nn.Fold
pytorch接口:
torch.nn.Fold(output_size, kernel_size, dilation=1, padding=0, stride=1)
对于\(shape=(N, C \times \prod(\text{kernel_size}), L)\)的输入,nn.Fold计算得到输出\(shape=(N, C, output\_size[0], output\_size[1])\)。
那么pytorch是怎么处理这个过程的呢?输入和输出的shape明显很难直观对应起来,我们查询源码,可以追溯到torch._C._nn.col2im函数,巧了,我们并不能在源码中找到其代码块。下面是参考程序员修练之路的博客给出的代码,我们对其进行验证:
def col2im(input, output_size, block_size):
p, q = block_size
sx = output_size[0] - p + 1
sy = output_size[1] - q + 1
result = np.zeros(output_size)
weight = np.zeros(output_size) # weight记录每个单元格的数字重复加了多少遍
col = 0
# 沿着行移动,所以先保持列(i)不动,沿着行(j)走
for i in range(sy):
for j in range(sx):
result[j:j + p, i:i + q] += input[:, col].reshape(block_size, order='F')
weight[j:j + p, i:i + q] += np.ones(block_size)
col += 1
return result / weight
这个Fold与上面的结果是差距较大的,待下次再研究吧 ……
nn.Fold的处理过程
明显上面的结果在nn.Fold上是不成立的,下面我们以下图展示其处理过程:
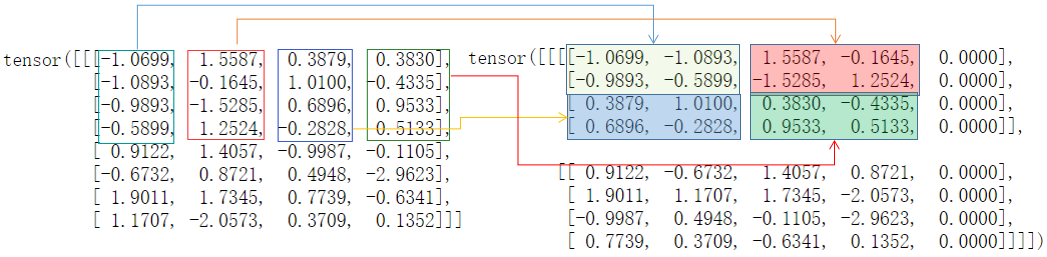
Fold的处理步骤如下:
- 第一步: 从输入中选择一个block某通道上的所有元素,将其reshape到指定的形状,这里的形状就是kernal_size。需要注意的是dim=1的维度与kernal_size的关系。
- 第二步: 在输出矩阵上填充reshape后的值。
- 第三步: 在输入矩阵上使用stride=1进行滑窗,在输出矩阵上,使用nn.Fold指定的stride进行滑窗,重复第一步、第二步。
完!


