External Attention:外部注意力机制
External Attention:外部注意力机制
作者: elfin
最近Transformer在CV领域的研究非常热,如ViT、BoTNet、External Attention等。使用Transformer的传统印象就是慢,这种慢还往往是我们不能接受的推理速度。在最近的实验中,基于单张2080TI,使用ResNet-34实现了batch_size为\(288\),图片大小为\(32\times200\),每个epoch的训练用时大约为:5个小时;同样的实验环境下,我实验了Swin Transformer的结构,在stage1实验卷积进行下采样(实现embedding的效果),stage2~stage4使用Swin block,block的数量分别为[2, 8, 2],stage5使用两层卷积进行简单的任务适配。这个结构在训练时,batch_size设置到\(42\),图片大小修改为\(32\times240\),每个epoch的训练用时大约为17个小时。Swin Transformer原作者声称其比卷积网络性能好,速度快,经过实验,实际上CNN的推理速度要比Transformer快,性价比方面Transformer确实是更高一些,但是其庞大的参数量也导致模型不太好训练。经过实验对比,在我的数据集上,Swin Transformer提升了将近7个百分点(epoch较少)。
虽然自注意力有那么多优点,但是这推理速度慢,耗资源的特点让我们这些缺硬件的渣渣很难受,然后就在前几天,突然看见清华、谷歌等大佬团队在做\(Transformer\rightarrow MLP\)的操作,当然这里不是指简单返祖现象,以清华的工作为例,它将二次复杂度降到线性复杂度,这个特性有成功吸引到我,所以,下面是清华的External Attention的相关情况。
1、External Attention
1.1 自注意力机制
首先回顾 self-attention机制,常见的自注意力如图所示:
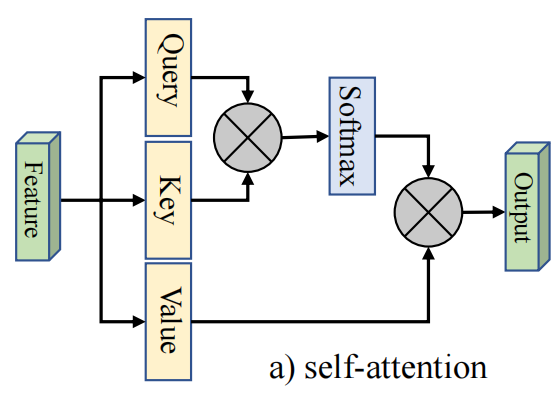
对于给定的输入特征图\(F\in \mathbb{R}^{N\times d}\),其中\(N\)是像素个数,\(d\)是特征维度;自注意力产生了查询矩阵\(Q\in \mathbb{R}^{N\times {d}'}\),键矩阵\(K\in \mathbb{R}^{N\times {d}'}\),和值矩阵\(V\in \mathbb{R}^{N\times d}\)。则自注意力机制的计算公式为:
简化版的注意力机制如下:

它的计算公式为:
基于上面的公式不难发现,注意力特征图是计算像素级的相似度,输出是输入的精确特征表示。
即使公式(3)(4)简化了,但是其计算复杂度仍然是\(O\left ( dN^{2} \right )\)。我们注意到随着特征图的增大,计算量的增大往往是我们无法接受的。以我上面的实验为例:
- \(32\times200\)的计算量为:\(192\times\left ( 32\times200 \right )^{2}=7864320000\)
- \(32\times240\)的计算量为:\(192\times\left ( 32\times240 \right )^{2}=11324620800\)
大约增加了\(40\%\)的计算量,这还只是一层,当然上面的计算方式有待商榷,但这也说明了计算量的增长是非常迅猛的,而且在高级语义特征图中,通道数会更大,一定程度上几乎会导致在所有层级上计算量都有很大的提升。当然这个增长是呈现指数倍率增长,所以我们需要提升精度的同时,提升速度、优化资源占用。
1.2 外部注意力机制
经过实验得知:自注意力机制是一个\(N-to-N\)的注意力矩阵,可视化像素之间的关系,可以发现这种相关性是比较稀疏的,即很多是冗余信息。因此清华团队提出了一个外部注意力模块。
它的注意力计算是在输入像素与一个外部记忆单元\(M\in \mathbb{R}^{S\times d}\)之间:
注意与自注意力机制不同,上式(5)是第\(i\)个像素点与\(M\)第\(j\)行的相似度。这里\(M\)是一个输入Input的可学习相关性参数,作为训练数据集的全局记忆。\(A\)是从先验信息得来的注意力特征图,Norm操作和自注意力一样。最终,通过\(A\)来更新\(M\)。
另外,我们用两种不同的记忆单元:\(M_{k}\)和\(M_{v}\)来增加网络的建模能力。
最终外部注意力机制的计算公式为:
经过上面的公式,外部注意力机制的复杂度是\(O(dSN)\)。这里的\(d\)、\(S\)是一个超参数,经过实验,作者发现\(S\)设置为64效果挺好。因此外部注意力机制比自注意力机制更高效,并且它可以直接应用于大尺寸的输入。
2、思考
- 计算量的降低和特征图的大小关系很大,这里的外部注意力机制的\(S\)设置为64,那么特征图的像素个数低于64时,实际它的计算量就更大。
- Swin Transformer是基于窗口进行自注意力计算的,window size作者使用的是7,像素个数\(N=49\),这也小于\(64\),所以同等情况下,外部注意力会有更大的计算量。
完!


