双指针的几个题

移动零

这道题相对较简单，官方之前的答案被人吐槽，现在好像更新了

这道题适合双指针操作，说白就是对数组下标的操作

思路就是，利用i遍历，然后利用j记录非零数的index位置

看java代码：

class Solution {
    public void moveZeroes(int[] nums) {
    	int j = 0;
        for (int i=0; i<nums.length; i++) {
            if (nums[i] != 0) {
                nums[j] = nums[i];
                if (i != j) nums[i] = 0;
                j++;
            }
        }
    }
}

其他帖子还有不同解法

class Solution {
    public void moveZeroes(int[] nums) {
        int index = 0;
        for (int num : nums) {
            if (num != 0) {
                nums[index++] = num;
            }
        }
        for (int i = index; i < nums.length; i++) {
            nums[i] = 0;
        }
    }
}

这种方法的思维十分清晰，就是用index来记录零的个数，把非零的一个个移到最前面来，最后再把剩下的变成零。执行的时间也十分得劲，我开始以为俩循环还不如第一个好来着。

然后看到第三种解法，暴力简单

class Solution(object):
    def moveZeroes(self, nums):
       for i in nums[:]://注意i不是下标是值，相当于foreach
           if i == 0 :
               nums.remove(0)
               nums.append(0)      

老哥的代码简洁通俗，遇零则删零往后补零。但考虑到数组remove操作是O(n),然后加上循环，整体的复杂度变为O(n^2)。跟前面的代码比就还差点意思。

逛国外网站

有用python写得比较好的

class Solution(object):
   def moveZeroes(self, nums):
    zero = 0  # records the position of "0"
    for i in xrange(len(nums)):
        if nums[i] != 0:
            nums[i], nums[zero] = nums[zero], nums[i]
            zero += 1

利用非零与零的交换，直接的写成a,b=b,a

方便

装水最多的容器

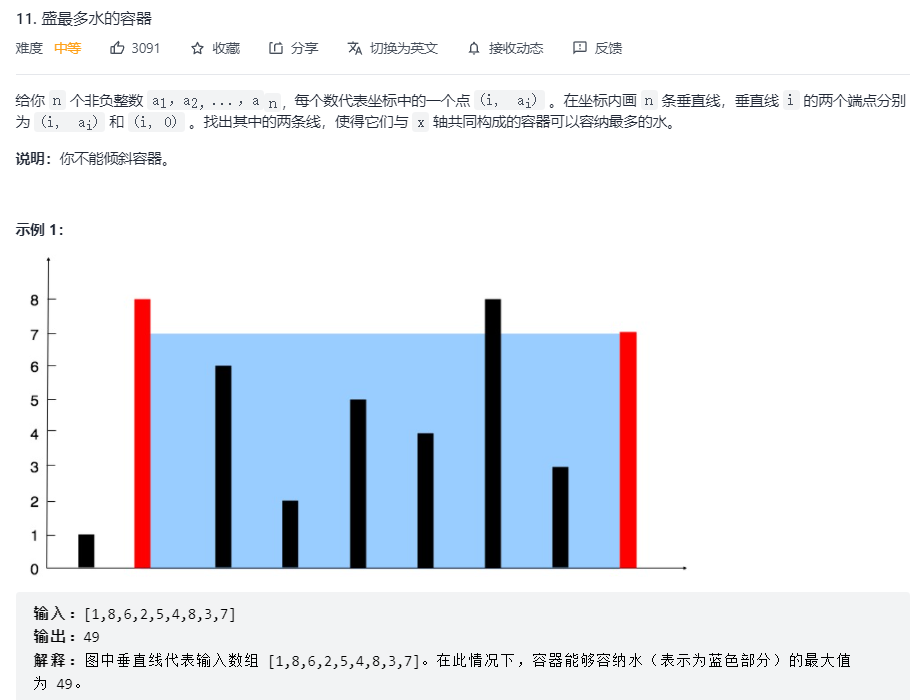
这道题最简单的做法就是枚举，把每个情况的面积都算出来，再比较。不过这样一来，时间复杂度就要是O(n^2)

先把代码打出来

class Solution {
    public int maxArea(int[] h) {
        int max = 0;
        for (int i = 0; i < h.length - 1; i++) {
            for (int j = i + 1; j < h.length; j++) {
                int area = (j - i) * Math.min(h[i], h[j]);
                max = Math.max(area, max);
            }
        }
        return max;
    }
}

这个放leetcode跑直接超时，但是思路至少是对的。

另外的解法就是跟上一道题一样，使用双指针。

从两边开始，逐渐向中间收紧，在最两边宽度无疑是最大的，就只需要考虑高度，所以长的不变，把短的一边向中间收，寻求更高的边。

注意求边的面积取决于宽度和低的一边的高度。

class Solution {
    public int maxArea(int[] h) {
        int max = 0;
        for (int i = 0, j = h.length - 1; i<j;) {
            int minheight = h[i] < h[j] ? h[i++] : h[j--];
            int area = (j - i + 1) * minheight;
            max = Math.max(area, max);
        }
        return max;
    }
}

求三数和

这题跟求两数和有相似之处，可以使用爆破进行

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> a=new ArrayList<List<Integer>>();
        for (int i = 0; i < nums.length-2; ++i) {
            if (i == 0 || (i > 0 && nums[i] != nums[i-1])) {
            for (int j = i + 1; j < nums.length-1; ++j) {
                for (int k = j + 1; k<nums.length; ++k){
                    if (nums[i] + nums[j] + nums[k] == 0) {                          
                         a.add(new ArrayList<Integer>(Arrays.asList(nums[i], nums[j], nums[k])));              
                    }
                }
            }
        }
            }
        return a;
    }
}

大致就这段代码，三层for献出了O(n^3)的极高复杂度。而且这代码不能够完全规避，比如当列表4个以上都是0时还是会重复，一时想不出有更好的写法。但爆破的路子大致就是这样，遍历每一种可能，直到匹配。

另外解法，就是采用双指针来处理

先固定好一个指针，在指针右边的第一个位置和最后一个位置设置指针，让俩之和为target，就是0减去第一个指针的内容，因为排好序，所以如果之和小于target，左边的指针往右移；大于的话就是有边的指针往左移，直到相遇。之后在让第一个指针一步步往右遍历，同样上述的操作。同时注意避免重复。

这样采用左右指针的时间复杂度将比爆破降低，为O(n^2)

class Solution {
    public List<List<Integer>> threeSum(int[] num) {
        Arrays.sort(num);
        List<List<Integer>> a = new LinkedList<>();
        for (int i = 0; i < num.length-2; i++) {
            if (num[i]>0) break;
            if (i == 0 || (i>0 && num[i] != num[i-1])){
                int l = i + 1, r = num.length - 1;
                while (l < r){
                    if (num[i]+num[l]+num[r] == 0) {
                    a.add(Arrays.asList(num[i],num[l],num[r]));
                    while (l<r && num[l]==num[l+1]) l ++;
                    while (l<r && num[r]==num[r-1]) r--;
                    l++;
                    r--;
                    }
                    else if (num[i]+num[l]+num[r]< 0) l++;
                    else  r--;
                    
                }
            }
        }
        return a;

    }
}

附上python写法

class Solution:
    def threeSum(self,nums):
        res = []
        nums.sort()
        for i in xrange(len(nums)-2):
            if (nums[i] > 0) : break
            if (i == 0 or (i>0 and nums[i] != nums[i-1])):
                l = i+1
                r = len(nums)-1
                
                while (l<r):
                    if (nums[i] + nums[l] + nums[r] == 0): 
                        res.append((nums[i],nums[l],nums[r]))
                        while (l<r and nums[l] == nums[l+1]) : l += 1
                        while (l<r and nums[r] == nums[r-1]) : r -= 1
                        l += 1; r -= 1
                    elif (nums[i] + nums[l] + nums[r] < 0) : l += 1
                    else : r -= 1
        return res

是否环形链表

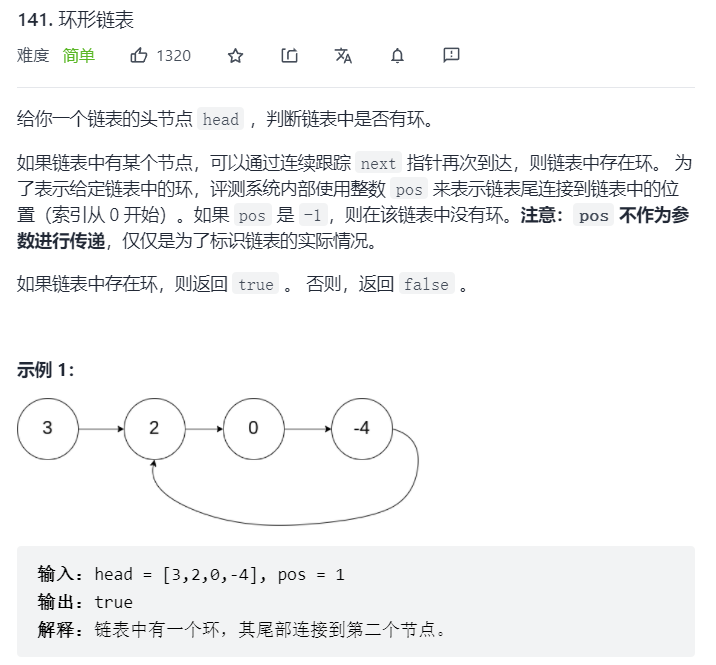
这道题不难，关键在于记住快慢指针的应用。找环的问题，归结于快慢不同的两个指针的相遇问题，若环，则遇；不环，则不遇。有篇文章的图解很好。

两指针都从头开始，慢的每次走一个节点，快的每次走两个节点，若存在闭环，则快的节点会跑回去与慢节点相遇。这不会存在跳过的问题

java代码：

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null)
            return false;
        ListNode f = head;
        ListNode s = head;
        while (f != null && f.next != null) {
            f = f.next.next;
            s = s.next;
            if (f == s) return true;
            
        }
        return false;
    }
}

python代码：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        if head==None:
            return False
        f = s = head
        while f.next != None and f.next.next != None :
            f = f.next.next
            s = s.next
            if f == s :
                return True
        return False

总结：这几个题的思路很重要，都是采用升维、空间换时间的策略。第一题与第四题相似，俩指针都在前头；第二题与第三题相似，就是有利用双指针从两边夹逼的意思。