原码 补码 反码 取反+1
计算机采用二进制计数，有符号整数的表示、存储和计算就是一个要解决的问题；
在这个问题上，计算机设计者选择了补码表示法。
在这之前，先看下另一种表示方法，符号及值表示法。
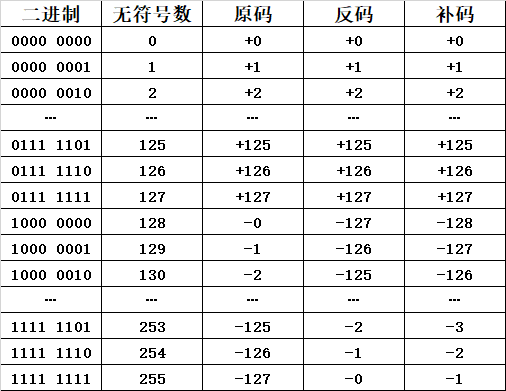
一个 n 位字可以表示从 0 ~ 2n-1 共 2n 个可能的值，如下表，无符号数列表示；表示负数的一种方法是用它的最高位表示符号，通常符号位为 0 表示正数，符号位为 1 表示负数；
有符号数的值可被表示为 (-1)s×M，这里 s 为数的符号位的值，M 为其数值部分；则其表示范围为 -(2n-1-1) ~ +(2n-1-1)，一个8位有符号数可以表示为 -127 ~ +127，如下表，原码列表示
但有个问题， 0000 0000 = +0、1000 0000 = -0，都表示0，只要一个唯一表示；因此计算机设计者选择了补码表示系统；该系统不仅能解决+0、-0的问题，还有另一个重大优势，
仅用加法器就可以进行包含负数的运算。
补码表示法，涉及到补数和模的概念；
举例，8位字长，10 - 2 = 10 + (-2) = (10 + (256-2)) mod 256 = (10 + 254) mod 256 ；所以 -2 和 +254 效果是一样的，那么 -2 就可以用 254来存储，即1111 1110，然后用加法器进行运算。
这里猜测下为什么是 -128。256个数，正负各半，各127个数；我们知道， 0 既不是正数又不是负数，那么还剩 2 个数要怎么安排？ 0000 0000、1000 0000；没说的，国际惯例，0000 0000 肯定表示 0
现在数的表示范围已经达到了 -127 ~ +127，那么还剩一个数，1000 0000 最高位是1， 划分到负数是很合理的，故只能是 -128；从另一个角度解释，对模=256来说，-128 运算等价于 +128，
如果划分到 +128，还会和前文（符号位为 1 表示负数）冲突。
取反+1
例如， -N 要存放到计算机，负数先进行求补运算，28 - N = 1 0000 00002 - N = 1 0000 00002 - 1 - N + 1 = 1111 11112 - N + 1
1111 11112 - N 对于计算机来说很容易实现，这也是补码的魅力；
另外对一个原码 2 次 取反+1，仍是本身；
例如，存 a = -126 时，求补存放；至于运算，计算机内部当作 +130 （1000 0010）用加法器处理；
当 printf %d 的 时候，检测到最高位为1，就进行一次取反+1拿到数值部分，然后添上符号输出 -126。
