算法进阶(三)——递归
递归与循环是程序设计中基础的环节,相对于循环,递归总是更神秘一些。
一、递归的实质
在程序中,递归的实现往往是通过程序压栈来实现的,执行方法时,如果仍然存在子递归,则将父级方法中的全部信息压入栈中,保存这部分数据;当子递归执行完毕后,从栈中取出父递归,并将子递归作为参数继续执行。
因此递归执行的过程其实就是压栈、出栈的过程
二、举例
从一个数组中找到它的最大值
参考牛客网题目:https://www.nowcoder.com/questionTerminal/10f59d86339041389c0b377d0af72300
1、遍历实现
遍历整个数组,依次比较每个数,从而找到最大值
1 fun getMaxNumber1(a: IntArray): Int { 2 if (a.isEmpty()) { 3 return -1 4 } 5 var max = a[0] 6 a.forEach { 7 if (it > max) { 8 max = it 9 } 10 } 11 return max 12 }
2、递归实现
从中间分割数组为左侧区间和右侧区间,然后左侧区间再次从中间分割,右侧区间也是如此
1 /** 2 * 通过分治递归的方式找到最大值 3 */ 4 fun getMaxNumber2(a: IntArray, left: Int, right: Int): Int { 5 if (left == right) { 6 return a[left] 7 } 8 val mid = (left + right) / 2 9 val leftMax = getMaxNumber2(a, left, mid) 10 val rightMax = getMaxNumber2(a, mid + 1, right) 11 return leftMax.coerceAtLeast(rightMax) 12 }
三、理解递归的实质
以上面的递归获取最大值来分析,假设数组为[1,3,6,2,8]
1、首先比较left==right条件,不满足,则计算mid = (left+right)/2 = (0+4)/2 = 2,即从下标为2的元素作为中间点,中间元素可以归到左侧数组,也可以归到右侧数组,这里以归属数组为例。此时左侧为[1,3,6],右侧[2,8]
2、执行val leftMax = getMaxNumber2(a, left, mid),这里leftMax的值是通过递归实现的,因此接下来需要执行leftMax等式右侧的递归,那么首先需要将当前方法中的信息保存到栈中(行数,方法中的传入的参数)。
这里 执行到第9行,且传入的left = 0 ,right = 4,因此压栈信息如下
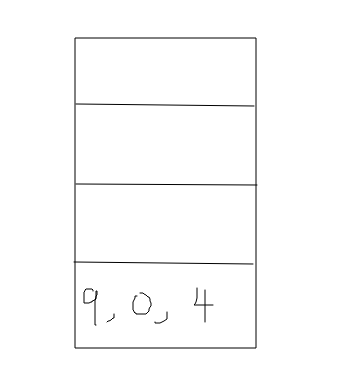
3、执行递归getMaxNumber(a,0,2),比较left == right,不满足,则计算mid = (left+right)/2 = 1,即从下标为1的元素作为中间点,左侧为[1,3],右侧为[2]。
4、执行val leftMax = getMaxNumber2(a, left, mid),left = 0,right = 1,而这里又是一个递归,那么在执行这个递归之前,需要将当前函数压栈。
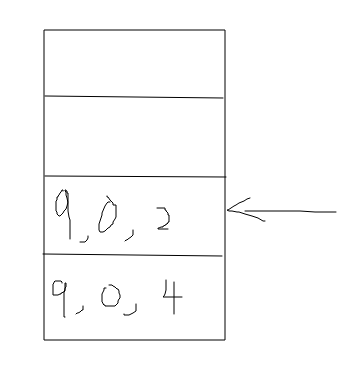
5、压栈依次类推,当递归执行中getMaxNumber2执行了return返回值时,假设getMaxNumber2(a,0,1)返回了对应的值,getMaxNumber2(a,2,2)也返回了对应值,此时就需要将入栈的方法信息执行出栈,恢复方法之前的状态,然后执行return leftMax.coerceAtLeast(rightMax)比较最大值
此时栈为:
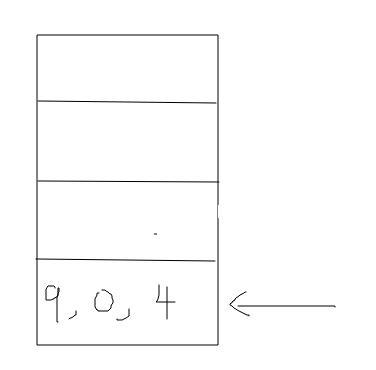
6、出栈依次类推,当所有的方法栈信息都出栈完成时,那么递归也就执行完毕了
四、递归复杂度
递归过程的复杂度是一个很常见的问题,相比较循环的复杂度分析,递归的复杂度分析要相对麻烦一点。
1、对于等分递归的分析
等分,即使把一个数组按相同的比例等分为几个子数组,那么就符合如下master公式:
T(N) = a*T(N/b)+O(N^d)
其中N为数组大小,a为常数倍数,b为等分的比例,O(N^d)表示在递归后执行的操作
以上面的求最大值递归为例:
对于左侧数组,需要执行N/2次遍历,而这样的操作需要执行两次。而在每次遍历的过程中,需要进行一次比较,这是常数操作,因此O(N^d) = O(N^0)即 = 1
则上面例子对应的公式为:
T(N) = 2T(N/2)+O(1)
符合master公式的前提下,可以通过下面来获取对应的时间复杂度
|
满足条件 |
时间复杂度 |
|
log(b,a)>d |
O(N^log(b,a)) |
|
log(b,a)=d |
O((N^d)*logN) |
|
log(b,a)<d |
O(N^d) |
套入到上面的例子中,T(N) = 2T(N/2)+O(1)。
其中a =2,b = 2,d = 0,那么log(2,2) = 1,即满足log(b,a)>d,那么对应的时间复杂度为O(N^log(b,a)),即复杂度为O(N)
2、非等分递归
对于非等分递归,我们不能再使用master公式来进行解决,而这种场景后面的算法中我们会分析到
五、归并排序的递归实现
归并排序其实就是递归实现的一种很好的应用。
归并排序算法的核心就是,将数组等分为两部分,先将左侧部分排好序,再将右侧部分排好序,然后将两部分有序的子数组进行合并。合并的时候,我们需要遍历整个数组进行比较。而核心就在于这里的合并过程
1、具体实现
1 @JvmStatic 2 fun mergeSort(a: IntArray, left: Int, right: Int) { 3 // 注意,递归需要特别注意边界值,否则会导致堆栈移除 4 if (left == right) { 5 return 6 } 7 // 求中间数,可以使用如下方式 8 val mid = left + ((right - left) shr 1) 9 // val mid = (left + right) / 2 10 mergeSort(a, left, mid) 11 mergeSort(a, mid + 1, right) 12 merge(a, left, mid, right) 13 } 14 15 /** 16 * 执行merge操作 17 */ 18 fun merge(a: IntArray, left: Int, mid: Int, right: Int) { 19 // 定义临时数组 20 val temp = IntArray(right - left + 1) 21 // 定义i,用于将排序后的值填入temp数组中 22 var i = 0 23 // 代表左侧数组下标 24 var p1 = left 25 // 代表右侧数组下标 26 var p2 = mid + 1 27 // 同时比较p1与p2对应的值的大小,如果a[p1]<= a[p2],则将a[p1]放入temp中,同时i的值+1,p1的值+1,p2不变,进入下一轮比较; 28 // 如果a[p1] > a[p2],则将a[p2]放入temp中,同时i的值+1,p2的值+1,p1不变,进入下一轮比较; 29 // 直到左右两个个数组达到边界,则停止比较 30 while (p1 <= mid && p2 <= right) { 31 temp[i++] = if (a[p1] <= a[p2]) a[p1++] else a[p2++] 32 } 33 34 // 表示右侧数组已达到边界值,此时将左侧数组剩余数值直接copy到temp即可 35 while (p1 <= mid) { 36 temp[i++] = a[p1++] 37 } 38 39 // 表示左侧数组已达到边界值,此时将右侧数组剩余数值直接copy到temp即可 40 while (p2 <= right) { 41 temp[i++] = a[p2++] 42 } 43 44 // 将临时temp的值,拷贝到原数组中 45 temp.forEachIndexed { index, i -> 46 a[left + index] = i 47 } 48 }
2、对应的master公式
T(N) = 2T(T/2)+O(N)
因此对应的master公式为:
T(N) = 2T(T/2)+O(N)
3、时间复杂度
对应到master公式中,则时间复杂度为:
O(N) = O((N^d)*logN) = O(N*logN)
4、空间复杂度
在实现中我们是临时生成不同区间的数组,其实可以等同于我们生成了一个全局的长度为N的数组,然后重复使用
因此额外空间复杂度为O(N)

