面试题:ConcurrentHashMap 在 Java7 和 8 有何不同?
Java 7 版本的 ConcurrentHashMap
我们首先来看一下 Java 7 版本中的 ConcurrentHashMap 的结构示意图:
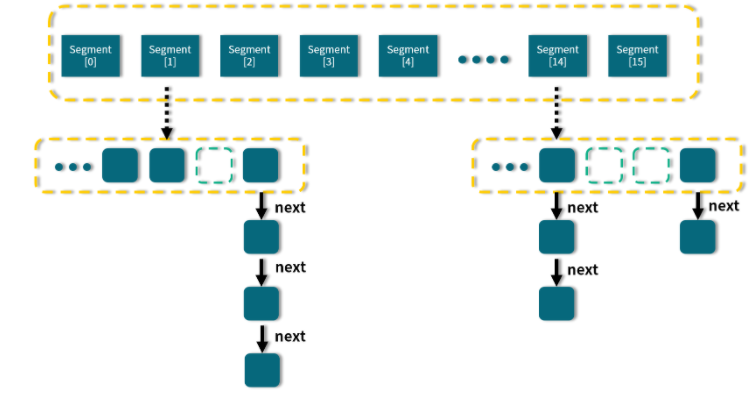
从图中我们可以看出,在 ConcurrentHashMap 内部进行了 Segment 分段,Segment 继承了 ReentrantLock,可以理解为一把锁,各个 Segment 之间都是相互独立上锁的,互不影响。相比于之前的 Hashtable 每次操作都需要把整个对象锁住而言,大大提高了并发效率。因为它的锁与锁之间是独立的,而不是整个对象只有一把锁。
每个 Segment 的底层数据结构与 HashMap 类似,仍然是数组和链表组成的拉链法结构。默认有 0~15 共 16 个 Segment,所以最多可以同时支持 16 个线程并发操作(操作分别分布在不同的 Segment 上)。16 这个默认值可以在初始化的时候设置为其他值,但是一旦确认初始化以后,是不可以扩容的。
Java 8 版本的 ConcurrentHashMap
在 Java 8 中,几乎完全重写了 ConcurrentHashMap,代码量从原来 Java 7 中的 1000 多行,变成了现在的 6000 多行,所以也大大提高了源码的阅读难度。而为了方便我们理解,我们还是先从整体的结构示意图出发,看一看总体的设计思路,然后再去深入细节。
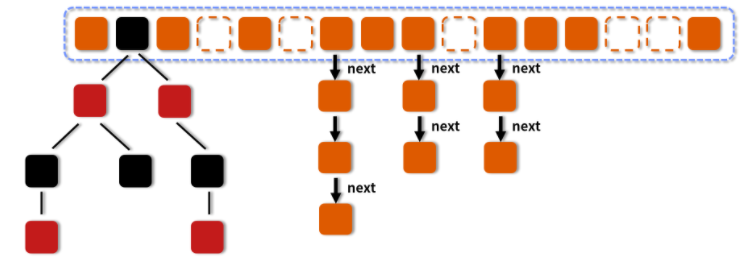
图中的节点有三种类型。
- 第一种是最简单的,空着的位置代表当前还没有元素来填充。
- 第二种就是和 HashMap 非常类似的拉链法结构,在每一个槽中会首先填入第一个节点,但是后续如果计算出相同的 Hash 值,就用链表的形式往后进行延伸。
- 第三种结构就是红黑树结构,这是 Java 7 的 ConcurrentHashMap 中所没有的结构,在此之前我们可能也很少接触这样的数据结构。
当第二种情况的链表长度大于某一个阈值(默认为 8),且同时满足一定的容量要求的时候,ConcurrentHashMap 便会把这个链表从链表的形式转化为红黑树的形式,目的是进一步提高它的查找性能。所以,Java 8 的一个重要变化就是引入了红黑树的设计,由于红黑树并不是一种常见的数据结构,所以我们在此简要介绍一下红黑树的特点。
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色,红黑树的本质是对二叉查找树 BST 的一种平衡策略,我们可以理解为是一种平衡二叉查找树,查找效率高,会自动平衡,防止极端不平衡从而影响查找效率的情况发生。
由于自平衡的特点,即左右子树高度几乎一致,所以其查找性能近似于二分查找,时间复杂度是 O(log(n)) 级别;反观链表,它的时间复杂度就不一样了,如果发生了最坏的情况,可能需要遍历整个链表才能找到目标元素,时间复杂度为 O(n),远远大于红黑树的 O(log(n)),尤其是在节点越来越多的情况下,O(log(n)) 体现出的优势会更加明显。
红黑树的一些其他特点:
- 每个节点要么是红色,要么是黑色,但根节点永远是黑色的。
- 红色节点不能连续,也就是说,红色节点的子和父都不能是红色的。
- 从任一节点到其每个叶子节点的路径都包含相同数量的黑色节点。
正是由于这些规则和要求的限制,红黑树保证了较高的查找效率,所以现在就可以理解为什么 Java 8 的 ConcurrentHashMap 要引入红黑树了。好处就是避免在极端的情况下冲突链表变得很长,在查询的时候,效率会非常慢。而红黑树具有自平衡的特点,所以,即便是极端情况下,也可以保证查询效率在 O(log(n))。
分析 Java 8 版本的 ConcurrentHashMap 的重要源码
Node 节点
我们先来看看最基础的内部存储结构 Node,这就是一个一个的节点,如这段代码所示:
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
volatile V val;
volatile Node<K,V> next;
// ...
}
可以看出,每个 Node 里面是 key-value 的形式,并且把 value 用 volatile 修饰,以便保证可见性,同时内部还有一个指向下一个节点的 next 指针,方便产生链表结构。
size 计算流程
size 计算实际发生在 put,remove 改变集合元素的操作之中
- 没有竞争发生,向 baseCount 累加计数
- 有竞争发生,新建 counterCells,向其中的一个 cell 累加计数
- counterCells 初始有两个 cell
- 如果计数竞争比较激烈,会创建新的 cell 来累加计数
public int size() {
long n = sumCount();
return ((n < 0L) ? 0 :
(n > (long)Integer.MAX_VALUE) ? Integer.MAX_VALUE :
(int)n);
}
final long sumCount() {
CounterCell[] as = counterCells; CounterCell a;
// 将 baseCount 计数与所有 cell 计数累加
long sum = baseCount;
if (as != null) {
for (int i = 0; i < as.length; ++i) {
if ((a = as[i]) != null)
sum += a.value;
}
}
return sum;
}
put 方法源码分析
put 方法的核心是 putVal 方法,为了方便阅读,我把重要步骤的解读用注释的形式补充在下面的源码中。我们逐步分析这个最重要的方法,这个方法相对有些长,我们一步一步把它看清楚。
final V putVal(K key, V value, boolean onlyIfAbsent) {
if (key == null || value == null) {
throw new NullPointerException();
}
//计算 hash 值
int hash = spread(key.hashCode());
int binCount = 0;
for (Node<K, V>[] tab = table; ; ) {
Node<K, V> f;
int n, i, fh;
//如果数组是空的,就进行初始化
if (tab == null || (n = tab.length) == 0) {
tab = initTable();
}
// 找该 hash 值对应的数组下标
else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
//如果该位置是空的,就用 CAS 的方式放入新值
if (casTabAt(tab, i, null,
new Node<K, V>(hash, key, value, null))) {
break;
}
}
//hash值等于 MOVED 代表在扩容
else if ((fh = f.hash) == MOVED) {
tab = helpTransfer(tab, f);
}
//槽点上是有值的情况
else {
V oldVal = null;
//用 synchronized 锁住当前槽点,保证并发安全
synchronized (f) {
if (tabAt(tab, i) == f) {
//如果是链表的形式
if (fh >= 0) {
binCount = 1;
//遍历链表
for (Node<K, V> e = f; ; ++binCount) {
K ek;
//如果发现该 key 已存在,就判断是否需要进行覆盖,然后返回
if (e.hash == hash &&
((ek = e.key) == key ||
(ek != null && key.equals(ek)))) {
oldVal = e.val;
if (!onlyIfAbsent) {
e.val = value;
}
break;
}
Node<K, V> pred = e;
//到了链表的尾部也没有发现该 key,说明之前不存在,就把新值添加到链表的最后
if ((e = e.next) == null) {
pred.next = new Node<K, V>(hash, key,
value, null);
break;
}
}
}
//如果是红黑树的形式
else if (f instanceof TreeBin) {
Node<K, V> p;
binCount = 2;
//调用 putTreeVal 方法往红黑树里增加数据
if ((p = ((TreeBin<K, V>) f).putTreeVal(hash, key,
value)) != null) {
oldVal = p.val;
if (!onlyIfAbsent) {
p.val = value;
}
}
}
}
}
if (binCount != 0) {
//检查是否满足条件并把链表转换为红黑树的形式,默认的 TREEIFY_THRESHOLD 阈值是 8
if (binCount >= TREEIFY_THRESHOLD) {
treeifyBin(tab, i);
}
//putVal 的返回是添加前的旧值,所以返回 oldVal
if (oldVal != null) {
return oldVal;
}
break;
}
}
}
addCount(1L, binCount);
return null;
}
通过以上的源码分析,我们对于 putVal 方法有了详细的认识,可以看出,方法中会逐步根据当前槽点是未初始化、空、扩容、链表、红黑树等不同情况做出不同的处理。
get 方法源码分析
get 方法比较简单,我们同样用源码注释的方式来分析一下:
public V get(Object key) {
Node<K,V>[] tab; Node<K,V> e, p; int n, eh; K ek;
//计算 hash 值
int h = spread(key.hashCode());
//如果整个数组是空的,或者当前槽点的数据是空的,说明 key 对应的 value 不存在,直接返回 null
if ((tab = table) != null && (n = tab.length) > 0 &&
(e = tabAt(tab, (n - 1) & h)) != null) {
//判断头结点是否就是我们需要的节点,如果是则直接返回
if ((eh = e.hash) == h) {
if ((ek = e.key) == key || (ek != null && key.equals(ek)))
return e.val;
}
//如果头结点 hash 值小于 0,说明是红黑树或者正在扩容,就用对应的 find 方法来查找
else if (eh < 0)
return (p = e.find(h, key)) != null ? p.val : null;
//遍历链表来查找
while ((e = e.next) != null) {
if (e.hash == h &&
((ek = e.key) == key || (ek != null && key.equals(ek))))
return e.val;
}
}
return null;
}
总结一下 get 的过程:
- 计算 Hash 值,并由此值找到对应的槽点;
- 如果数组是空的或者该位置为 null,那么直接返回 null 就可以了;
- 如果该位置处的节点刚好就是我们需要的,直接返回该节点的值;
- 如果该位置节点是红黑树或者正在扩容,就用 find 方法继续查找;
- 否则那就是链表,就进行遍历链表查找。
Java 8 数组(Node) +( 链表 Node | 红黑树 TreeNode ) 以下数组简称(table),链表简称(bin)
- 初始化,使用 cas 来保证并发安全,懒惰初始化 table
- 树化,当 table.length < 64 时,先尝试扩容,超过 64 时,并且 bin.length > 8 时,会将链表树化,树化过程会用 synchronized 锁住链表头
- put,如果该 bin 尚未创建,只需要使用 cas 创建 bin;如果已经有了,锁住链表头进行后续 put 操作,元素添加至 bin 的尾部
- get,无锁操作仅需要保证可见性,扩容过程中 get 操作拿到的是 ForwardingNode 它会让 get 操作在新table 进行搜索
- 扩容,扩容时以 bin 为单位进行,需要对 bin 进行 synchronized,但这时妙的是其它竞争线程也不是无事可做,它们会帮助把其它 bin 进行扩容,扩容时平均只有 1/6 的节点会把复制到新 table 中
- size,元素个数保存在 baseCount 中,并发时的个数变动保存在 CounterCell[] 当中。最后统计数量时累加即可
对比Java7 和Java8 的异同和优缺点
数据结构
Java 7 采用 Segment 分段锁来实现,而 Java 8 中的 ConcurrentHashMap 使用数组 + 链表 + 红黑树,在这一点上它们的差别非常大。
并发度
Java 7 中,每个 Segment 独立加锁,最大并发个数就是 Segment 的个数,默认是 16。
但是到了 Java 8 中,锁粒度更细,理想情况下 table 数组元素的个数(也就是数组长度)就是其支持并发的最大个数,并发度比之前有提高。
保证并发安全的原理
Java 7 采用 Segment 分段锁来保证安全,而 Segment 是继承自 ReentrantLock。
Java 8 中放弃了 Segment 的设计,采用 Node + CAS + synchronized 保证线程安全。
遇到 Hash 碰撞
Java 7 在 Hash 冲突时,会使用拉链法,也就是链表的形式。
Java 8 先使用拉链法,在链表长度超过一定阈值时,将链表转换为红黑树,来提高查找效率。
查询时间复杂度
Java 7 遍历链表的时间复杂度是 O(n),n 为链表长度。
Java 8 如果变成遍历红黑树,那么时间复杂度降低为 O(log(n)),n 为树的节点个数。


