插入原理参考《算法导论》,删除原理请参考以下链接:https://www.youtube.com/watch?v=fKubKYzwDl0
代码实现如下
声明一个B树类,随机生成对应关键字的数据data
template <int t> class BTree { public: typedef struct _BNode{ _BNode(bool _leaf) :n(0), leaf(_leaf), p(NULL) { for (int i = 0; i < 2 * t; i++) c[i] = NULL; } std::pair<int, int> e[2 * t - 1];//e.first是关键字,e.second是数据 _BNode *c[2 * t];//2*t个子节点 bool leaf;//true代表叶子(没有子结点,本身就足以容纳关键数据),false代表结点 int n;//代表关键字个数 _BNode *p;//父结点 }BNode, *pBNode; BTree(int n) { seed = Seed(log2(n), 4); root = new BNode(true); } void Insert(BNode *x, int k, int d); std::pair<BNode *, int> Search(BNode *x, int k); std::pair<BNode *, int> Prev(int k); std::pair<BNode *, int> Next(int k); void Delete(BNode *x, int k); void Empty(); void Print(BNode *x);//顺序输出 void Print_tree(BNode *x);//层次输出 int Hash(int k); BNode *Root() { return root; } ~BTree() { Empty(); } private: void Split_child(BNode *x, int i, BNode *y); void Insert_directly(BNode *x, int k, int d); int Seed(int n, int iCheck); int _Hash(int k, int w, int p); int seed; BNode *root; };
对应的成员函数实现
Insert函数,原理来自《算法导论》
template <int t> void BTree<t>::Insert(typename BTree<t>::BNode *x, int k, int d) { BNode *r = root, *s; if (r->n == 2 * t - 1) { s = new BNode(false); root = s; s->c[0] = r; Split_child(s, 0, r); Insert_directly(s, k, d); } else Insert_directly(r, k, d); }
两个辅助函数
template<int t> void BTree<t>::Split_child(typename BTree<t>::BNode *x, int i, typename BTree<t>::BNode *y) {//分裂y,并在x->c[i]处插入y结点 int j; BNode *z = new BNode(y->leaf); //z结点,是x结点的右子结点 z->n = t - 1; for (j = 0; j < t - 1; j++) z->e[j] = y->e[j + t];//复制关键字 if (!y->leaf) //y是结点 for (j = 0; j < t; j++) { z->c[j] = y->c[j + t];//复制子结点 z->c[j]->p = z; } //y结点,是x结点的左子结点 y->n = t - 1; //在x结点中增加一个子结点z,保证x->n<=2*t-1,并且x结点的i处是y for (j = x->n; j >= i + 1; j--) x->c[j + 1] = x->c[j]; x->c[i + 1] = z; for (j = x->n - 1; j >= i; j--) x->e[j + 1] = x->e[j]; x->e[i] = y->e[t - 1]; x->n++; //更新父结点信息 z->p = y->p = x; } template <int t> void BTree<t>::Insert_directly(typename BTree<t>::BNode *x, int k, int d) { int i = x->n - 1; if (x->leaf) {//同一高度插入关键字k while (i >= 0 && k < x->e[i].first) {//调用此函数前,保证了x->n<2*t-1 x->e[i + 1] = x->e[i]; i--; } x->e[i + 1] = std::make_pair(k, d); x->n++; } else {//结点满了 while (i >= 0 && k < x->e[i].first) i--; i = i + 1; if (x->c[i]->n == 2 * t - 1) { Split_child(x, i, x->c[i]); if (k > x->e[i].first) i++; } Insert_directly(x->c[i], k, d); } }
Search函数,查找某个关键字
template <int t> typename std::pair<typename BTree<t>::BNode *, int> BTree<t>::Search(typename BTree<t>::BNode *x, int k) {//返回<结点指针,关键字索引> int i = 0; while (i<x->n && k>x->e[i].first) i++; if (i < x->n && k == x->e[i].first) return std::make_pair(x, i); if (x->leaf) //叶子 return std::make_pair<BNode *,int>(NULL, -1); else return this->Search(x->c[i], k); }
Next和Prev函数,后继和前驱
template <int t> typename std::pair<typename BTree<t>::BNode *, int> BTree<t>::Prev(int k) {//返回<结点指针,关键字索引> typename std::pair<BNode *, int> p = this->Search(root, k); BNode *x = p.first, *y; int i = p.second; if (x == NULL) return p; if (x->c[i]) {//左子结点存在,优先查找 x = x->c[i]; while (!x->leaf) x = x->c[x->n]; i = x->n; } else if (i > 0) {//结点内还有比自己小的,次优先查找 } else {//父结点查找 while (x->p) { y = x; x = x->p; for (i = 0; i < x->n + 1; i++) if (x->c[i] == y && i != 0) return std::make_pair(x, i - 1); } if (x == p.first || i == x->n + 1) return std::make_pair<BNode *, int>(NULL, -1); } return std::make_pair(x, i - 1); } template <int t> typename std::pair<typename BTree<t>::BNode *, int> BTree<t>::Next(int k) {//返回<结点指针,关键字索引> typename std::pair<BNode *, int> p = this->Search(root, k); BNode *x = p.first, *y; int i = p.second; if (x== NULL) return p; if (x->c[i + 1]) {//右子结点存在,优先查找 x = x->c[i + 1]; while (!x->leaf) x = x->c[0]; i = 0; } else if (i < x->n - 1) //结点内还有比自己大的,次优先查找 i++; else {//父结点查找 while (x->p) { y = x; x = x->p; for (i = 0; i < x->n + 1; i++) if (x->c[i] == y && i != x->n) return std::make_pair(x, i); } if (x == p.first || i == x->n + 1) return std::make_pair<BNode *, int>(NULL, -1); } return std::make_pair(x, i); }
Delete删除函数,原理参考链接视频
template <int t> void BTree<t>::Delete(typename BTree<t>::BNode *x, int k) { typename std::pair<BNode *, int> p = this->Search(x, k); BNode *lSib, *rSib; int i = p.second, j; x = p.first;//x含有目标关键字k if (x == NULL) return; if (x->leaf) {//x是叶子,那么左右兄弟必然也是叶子 //定位左右兄弟lSib, rSib if (x->p) { for (j = 0; j < x->p->n + 1; j++) if (x->p->c[j] == x) break; lSib = (j - 1 > -1) ? x->p->c[j - 1] : NULL; rSib = (j + 1 < x->p->n + 1) ? x->p->c[j + 1] : NULL; } else lSib = rSib = NULL; if (x == root && x->n == 1) { delete x; root = NULL; } else if (x->n >= t) {//case 1,x有至少t个关键字,则直接删除 for (j = i; j < x->n - 1; j++) x->e[j] = x->e[j + 1]; x->n--; } else if (x->n == t - 1) { //case 2a,x仅有t-1个关键字,并且lSib或rSib兄弟右至少t个关键字 if (rSib && rSib->n >= t) {//是右兄弟存在,父结点中对应的关键字是x->p->e[j]->first x->e[x->n] = x->p->e[j];//父结点中x->p->e[j]下降到x x->p->e[j] = rSib->e[0];//右兄弟rSib->e[0]上升到x->p //x->p没有变化,无需调整,所有变化不影响父结点 x->n++;//x增加一个关键字 for (i = 0; i < rSib->n - 1; i++) rSib->e[i] = rSib->e[i + 1];//删除移走的关键字rSib->e[0] rSib->n--; } else if (lSib && lSib->n >= t) {//是左兄弟存在,父结点中对应的关键字是x->p->e[j-1]->first for (i = 0; i < x->n; i++) x->e[i + 1] = x->e[i]; x->e[0] = x->p->e[j - 1];//父结点x->p->e[j-1]下降到x x->p->e[j - 1] = lSib->e[lSib->n - 1];//左兄弟lSib->e[lSib->n - 1]上升到x->p //x->p同上 x->n++; lSib->n--; } else {//case 2b,此时必定是左或右兄弟都仅有t-1个关键字 if (rSib) {//rSib合并到x x->e[x->n] = x->p->e[j];//父结点中关键字x->p->e[j]下降到x for (i = 0; i < rSib->n; i++) x->e[x->n + 1 + i] = rSib->e[i]; //调整x->p,保证x->p->c[j]是x for (i = j; i < x->p->n - 1; i++) x->p->e[i] = x->p->e[i + 1]; for (i = j; i < x->p->n; i++) x->p->c[i] = x->p->c[i + 1]; x->p->c[j] = x; x->p->n--; x->n = x->n + 1 + rSib->n; delete rSib; } else if (lSib){//x合并到lSib lSib->e[lSib->n] = x->p->e[j - 1];//父结点中关键字x->p->e[j-1]下降到lSib for (i = 0; i < x->n; i++) lSib->e[lSib->n + 1 + i] = x->e[i]; //调整x->p,保证x->p->c[j-1]是lSib for (i = j - 1; i < x->p->n - 1; i++) x->p->e[i] = x->p->e[i + 1]; for (i = j - 1; i < x->p->n; i++) x->p->c[i] = x->p->c[i + 1]; x->p->c[j - 1] = lSib; x->p->n--; lSib->n = lSib->n + 1 + x->n; delete x; x = lSib; } if (x->p->n == 0) {//更新父结点 BNode *readyToDel = x->p; if (x->p == root) root = x; if (x->p->p) { for (i = 0; i < x->p->p->n + 1; i++) if (x->p->p->c[i] == x->p) break; x->p->p->c[i] = x; } x->p = x->p->p; delete readyToDel; } } this->Delete(x, k);//递归删除 } } else {//x是内结点 lSib = x->c[i];//左子结点 rSib = x->c[i + 1];//右子结点 if (lSib->n >= t) {//case 3a,左子结点至少有t个关键字 p = this->Prev(k);//前驱 x->e[i] = p.first->e[p.second];//替换掉关键字k this->Delete(p.first, p.first->e[p.second].first);//递归删除前驱值 } else if (rSib->n >= t) {//case 3b,右子结点至少有t个关键字 p = this->Next(k); x->e[i] = p.first->e[p.second]; this->Delete(p.first, p.first->e[p.second].first); } else {//case 3c,此时必定是左或右结点仅有t-1个关键字,直接合并两个结点 //合并到lSib lSib->e[lSib->n] = x->e[i];//关键字k下降到lSib for (j = 0; j < rSib->n; j++) lSib->e[lSib->n + 1 + j] = rSib->e[j];//rSib合并到lSib if (!lSib->leaf) { for (j = 0; j < rSib->n + 1; j++) { lSib->c[lSib->n + 1 + j] = rSib->c[j]; //调整父结点 rSib->c[j]->p = lSib; } } lSib->n = lSib->n + 1 + rSib->n; //调整x结点,保证x->c[i]是lSib for (j = i; j < x->n - 1; j++) x->e[j] = x->e[j + 1]; for (j = i; j < x->n; j++) x->c[j] = x->c[j + 1]; x->c[i] = lSib; x->n--; delete rSib; if (x->n == 0) {//更新父结点 if (x == root) root = lSib; if (x->p) {//替换x->p-c[?]的子结点 for (j = 0; j < x->p->n + 1; j++) if (x->p->c[j] == x) break; x->p->c[j] = lSib; } lSib->p = x->p; delete x; } this->Delete(lSib, k); } } }
两个打印函数
void BTree<t>::Print(typename BTree<t>::BNode *x) { if (x == NULL) return; for (int i = 0; i < x->n; i++){ if (!x->leaf) Print(x->c[i]); printf("%c-%d%-02s", x->e[i].first, x->e[i].second, " "); } if (!x->leaf) Print(x->c[x->n]); } template <int t> void BTree<t>::Print_tree(typename BTree<t>::BNode *x) { if (x == NULL) return; for (int i = 0; i < x->n; i++) printf("%c-%d%-02s", x->e[i].first, x->e[i].second, " "); if (x->p) printf("from %c\n", x->p->e[0].first); else printf("it is root\n"); if (!x->leaf) //结点 for (int i = 0; i <= x->n; i++) Print_tree(x->c[i]); }
数据随机生成函数,采用乘法随机,原理参考之前我发的随笔。
template <int t> int BTree<t>::Hash(int k) { return _Hash(k, 32, seed); }
template <int t> int BTree<t>::Seed(int n, int iCheck) { int iStart = n / iCheck, prime = (iStart == 1) ? 2 : iStart; assert(iCheck >= 0 && iCheck <= 8); //odd起始要跳过已经判断了的奇数 for (int j = 0, odd = (iStart % 2 == 0) ? iStart / 2 : (iStart - 1) / 2 + 1; j < 8 - iCheck; odd++) { //生成一个素数 bool fPrime = true; for (int k = 2; k <= sqrt(prime); k++) if (prime % k == 0) { fPrime = false; break; } if (fPrime) //记录素数 j++; prime = odd * 2 + 1;//待判断的奇数 } return prime - 2; } template <int t> int BTree<t>::_Hash(int k, int w, int p) { __int64 s = (sqrt(5) - 1) / 2 * pow(2, w); __int64 r0 = s * k % (__int64)pow(2, w); return r0 / pow(2, w - p);//高p位有效位 }
empty函数
template <int t> void BTree<t>::Empty(){ while (root && root->n != 0) { printf("%c deleted\n", root->e[0].first); this->Delete(root, root->e[0].first); Print(root); printf("\n"); } }
数据测试
int key[] = { 'F','S','Q','K','C','L','H','T','V','W','M','R','N','P','A','B','X','Y','D','Z','E'};
Main函数
int main() { //while (true) {//用于测试是否存在内存泄露 int key[] = { 'F','S','Q','K','C','L','H','T','V','W','M','R','N','P','A','B','X','Y','D','Z','E'}; BTree<2> btree(LENGTH(key)); for (int i = 0; i < LENGTH(key); i++) btree.Insert(btree.Root(), key[i], btree.Hash(key[i])); btree.Print_tree(btree.Root()); printf("\n"); btree.Print(btree.Root()); printf("\n"); std::pair<BTree<2>::BNode *, int> next, prev; printf("Next/Next函数测试\n"); for (int i = 0; i < LENGTH(key); i++) { next = btree.Next(key[i]); prev = btree.Prev(key[i]); printf("%c's next is %c, prev is %c\n", key[i], next.first ? next.first->e[next.second].first : '.', prev.first ? prev.first->e[prev.second].first : '.'); } /* printf("Delete函数测试\n"); for (int i = 0; i < LENGTH(key); i++) { printf("i=%d, delete %c\n", i, key[i]); btree.Delete(btree.Root(), key[i]); btree.Print(btree.Root()); printf("\n"); } */ printf("对象释放....\n"); //} return 0; }
输出结果


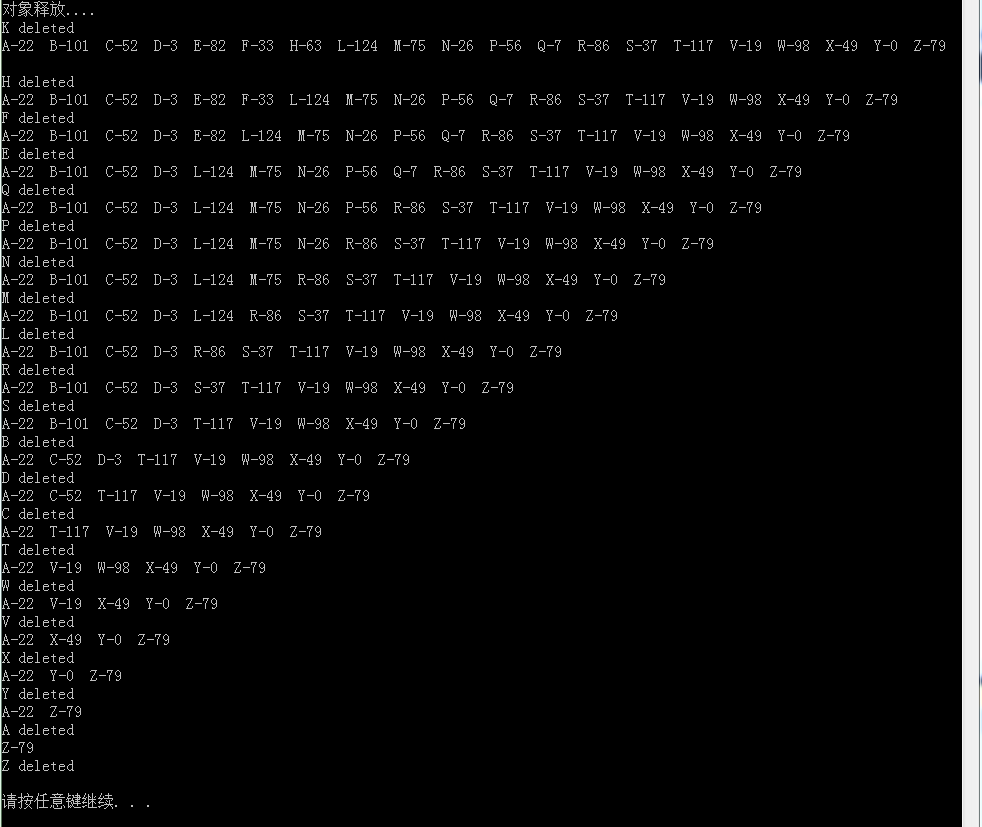
对应正确结果图
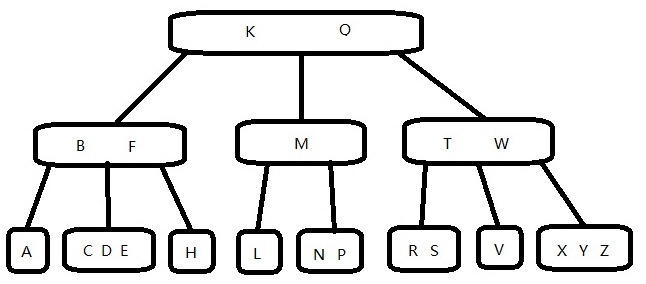
所有代码均经过测试,结果正确!!!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号