动态规划之最优二叉树

原理来自于《算法导论》，其实和矩阵的动态规划基本一样，所以这里就不作阐述了。

直接上代码，通过构造了最优的root数组后，很容易再创建一个二叉树（这一小部分大家可以自己理解后试试）。

关于代码的说明，因为书上给出的是伪代码，数组并没有采用C语言格式，下标不是从0开始，所以算法和root数组我做了调整，让其尊重了C语言数组格式。最后解释最优二叉树时，需要把C语言形式的root数组转换为原来书上的数组格式，简单的做法是下标加1后显示就行了。

定多个预处理函数

#define LENGTHP (sizeof(p)/sizeof(p[0]))
#define LENGTHQ (sizeof(q)/sizeof(q[0]))
#define DYNAMICDEBUG(TY, NM, N)                                           \
            printf("Showing type:" #TY ", variable name:" #NM "\n");      \
            showbst<TY>((NM),(N))

optimalbst函数，生成二维数组root, p, q，并填充数据。注意：此时的root数组内容是下标从0开始的。

int **optimalbst(float *p, float *q, int lengthp, int lengthq, float ***e, float ***w) {//返回root，记录着对应的索引
    if (lengthp <= 0 || lengthq <= 0) return NULL;
    int **root = new int *[lengthp], i, j;
    float t;
    *e = new float *[lengthq];
    *w = new float *[lengthq];
    for (i = 0; i < lengthp; i++)
        root[i] = new int[lengthp];
    for (i = 0; i < lengthq; i++) {
        (*e)[i] = new float[lengthq];
        (*w)[i] = new float[lengthq];
    }
    //初始化数据
    for (i = 0; i < lengthp; i++)
        for (j = 0; j < lengthp; j++)
            root[i][j] = -1;
    for (i = 0; i < lengthq; i++)
        for (j = 0; j < lengthq; j++)
            (*e)[i][j] = (*w)[i][j] = -1;
    //动态规划算法
    for (i = 0; i < lengthq; i++)
        (*e)[i][i] = (*w)[i][i] = q[i];
    for (int l = 1; l <= lengthp; l++)
        for (i = 1; i <= lengthp - l + 1; i++) {
            j = i + l - 1;
            (*w)[i - 1][j] = (*w)[i - 1][j - 1] + p[j - 1] + q[j];//i下标全部调整，j下标保持
            for (int r = i; r <= j; r++) {
                t = (*e)[i - 1][r - 1] + (*e)[r][j] + (*w)[i - 1][j];
                if ((*e)[i - 1][j] == -1.0f || t < (*e)[i - 1][j]) {
                    (*e)[i - 1][j] = t;
                    root[i - 1][j - 1] = r - 1;
                }
            }
        }
    return root;
}

printfbst函数，解释root数组。注意：此时要将下标转换为原始数据的标号！！！

void printfbst(int **root, int i, int j, int n) {
    if (i == 0 && j == n - 1)
        printf("k%d是根\n", root[i][j]+1);
    if (i < j)
    {
        int index = root[i][j];
        if (index != i)
            printf("k%d是k%d的左节点\n", root[i][index - 1] + 1, index + 1);
        printfbst(root, i, index - 1, n);
        if (index != j)
            printf("k%d是k%d的右节点\n", root[index + 1][j] + 1, index + 1);
        printfbst(root, index + 1, j, n);
    }
    else if (i == j)
    {
        printf("d%d是k%d的左节点\n", i, i + 1);
        printf("d%d是k%d的右节点\n", i + 1, i + 1);
    }
    else
        printf("d%d是k%d的右节点\n", j + 1, j + 1);
}

数据录入，从这里就看的出p数组的下标不满足C语言数组性质，所以我作了修改，让其满足，这样录入数据就非常方便了！！！

float p[] = { 0.15,0.1,0.05,0.1,0.2 }, q[] = { 0.05,0.1,0.05,0.05,0.05,0.1 }

完整的main函数，用于测试

int main()
{
    float p[] = { 0.15,0.1,0.05,0.1,0.2 }, q[] = { 0.05,0.1,0.05,0.05,0.05,0.1 }, **e, **w;//k1 - k5, d0-d5
    int **root;//root保存的是数组下标
    root = optimalbst(p, q, LENGTHP, LENGTHQ, &e, &w);
    DYNAMICDEBUG(float, e,LENGTHQ);
    DYNAMICDEBUG(float, w, LENGTHQ);
    DYNAMICDEBUG(int, root, LENGTHP);
    printf("解释最优二叉树，数组下标转换为实际的k1-k5, d0-d5\n");
    printfbst(root, 0, LENGTHP-1, LENGTHP);
    freebst<int>(root, LENGTHP);
    freebst<float>(e, LENGTHQ);
    freebst<float>(w, LENGTHQ);
    return 0;
}

几个辅助函数，用于测试

template <typename T>
void freebst(T **p, int n) {
    for (int i = 0; i < n; i++)
        delete[] p[i];
    delete[] p;
}

template <typename T>
void showbst(T **p, int n) {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++)
            if ((float)p[i][j] != -1.0f)
                printf("%.2f ", (float)p[i][j]);
            else
                printf("%-05s", " ");
        printf("\n");
    }
    printf("\n");
}

测试结果：

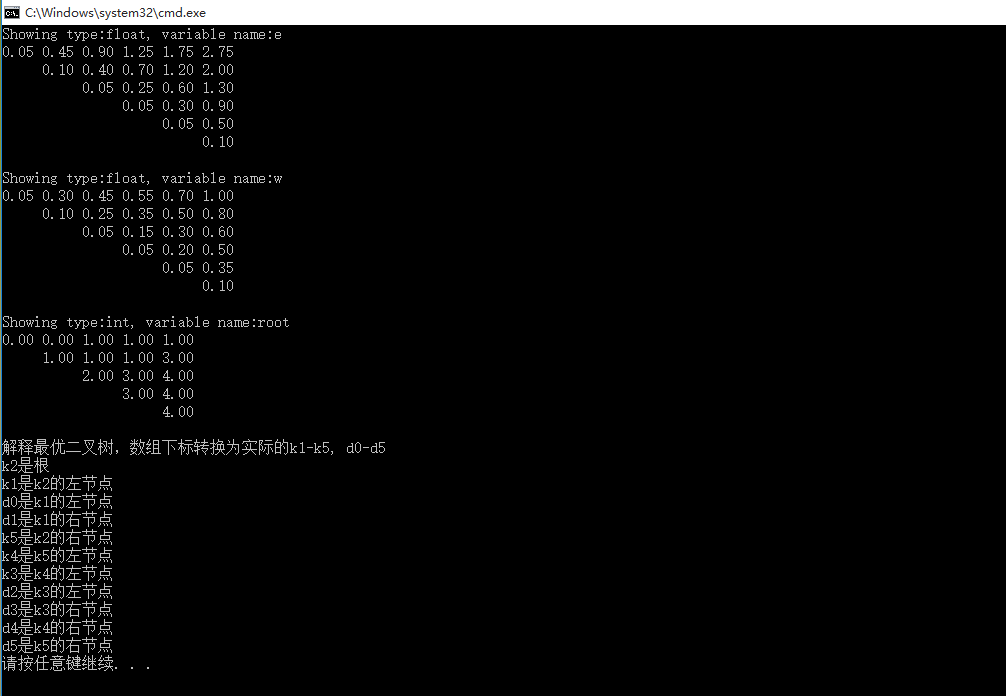
上图分别对应书上的结果图

e数组， w数组，以及root数组。注意：再三强调，经过修改，root数组内容是指向数组下标的，而非实际的数据标号。

 

 

 

再看对应的二叉树解释

 

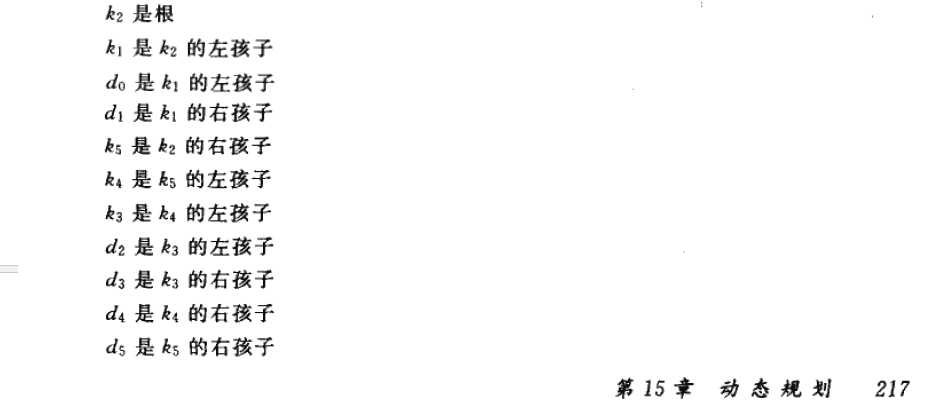
所有代码经过测试，结果正确！！！