动态规划之多矩阵乘积

算法原理请参考《算法导论》，因为算法这东西千篇一律，关键还是实现和理解，这里只提几个关键点，帮助大家理解。

1. 为什么需要动态规划？

比如矩阵A是p x q大小，矩阵B是q x r大小，很明显，得到的矩阵C是p x r大小，其中花费的时间必定是p*q*r。这只是两个矩阵，如果存在N个矩阵需要算其乘积呢？那么就需要用到动态规划了，比如A(p x q), B(q x r), C(r x l)这三个矩阵相乘。如果不规划，那么花费的时间是A*B=p*q*r，然后再乘以C，还需要额外花费p*r*l时间。但有可能B*C先乘，然后再乘以A，这样花费的时间最少。以此推广到N个矩阵相乘。这就是动态规划的原因！！！

2. 为了帮助大家理解《算法导论》中的算法，这里我给大家讲解下数组p。比如A(a x b), B(b x c), C(c x d)这三个矩阵，那么p数组的内容是p[]={a,b,c,d}，书上因为没有采用C语言数组，所以下标从1开始，但是这里我给出下标从0开始的数组p，这样矩阵A可以用p[0] x p[1] 表示，那么推广到N个矩阵，矩阵A:i的维度是p[i] x p[i+1] （所以，书上给出的伪代码需要做一些下标调整，包括算法）

下面是代码部分

matric_free函数，内存回收

template <int p>
void matric_free(int **C) {
    for (int i = 0; i < p; i++)
        delete[] C[i];
    delete[] C;
}

matric_show函数，打印矩阵，默认值为-1时，表示未使用，则不打印。

template <int p, int q>
void matric_show(int **A) {
    for (int i = 0; i < p; i++) {
        for (int j = 0; j < q; j++)
            if (A[i][j] == -1)
                printf("%-04s", " ");
            else
                printf("%-04d ", A[i][j]);
        printf("\n");
    }
}

matric_multiply函数，这个是任意两个矩阵相乘，从代码也可以推出来，任意两个矩阵相乘花费的时间是p*q*r

template <int p, int q, int r>
int **matric_multiply(int A[p][q], int B[q][r]) {
    int **C = new int *[p];
    for (int i = 0; i < r; i++)
        C[i] = new int[r];
    for (int i = 0; i<p; i++)
        for (int j = 0; j < r; j++) {
            C[i][j] = 0;
            for (int k = 0; k < q; k++)
                C[i][j] += A[i][k] * B[k][j];
        }
    return C;
}

matric_optimal函数，通过传入数组p（构建原理，已经在上面的关键点中提到了）,length参数代表数组p长度，实际上，数组p会多一个元素出来，所以真实构建的m和s是length-1，由于下标通通改用了C语言形式，所以代码我做了调整

template <int length>
void matric_optimal(int *p, int ***m, int ***s) {
    int n = length - 1, q;
    if (n < 2) return;//至少两个矩阵
    *m = new int *[n];
    *s = new int *[n];
    for (int i = 0; i < n; i++) {//生成m, s对应的二维数组
        (*m)[i] = new int[n];
        (*s)[i] = new int[n];
    }
    //初始化
    for (int i=0;i<n;i++)
        for (int j = 0; j < n; j++) 
            (*m)[i][j] = (*s)[i][j] = -1;//-1表示未使用
    for (int i = 0; i < n; i++)
        (*m)[i][i] = 0;
    for (int l = 1; l <= n; l++) //这里针对C语言数组，做了改变
        for (int i = 0; i < n - l + 1; i++)
        {
            int j = i + l - 1;
            for (int k = i; k <j; k++) {
                q = (*m)[i][k] + (*m)[k + 1][j] + p[i] * p[k+1] * p[j+1];//这里针对C语言数组做了改变，原因很简单，因为数组下标不能取-1，所以需要修改
                if ((*m)[i][j]==-1 || q < (*m)[i][j]) {
                    (*m)[i][j] = q;
                    (*s)[i][j] = k;//保留k值，方便输出
                }
            }
        }
}

另一个版本是递归版本，是recursive_matric_optimal函数。

int recursive_matric_optimal(int *p, int ***m, int ***s, int i, int j) {
    int q, n;
    if (i == j) return 0;
    if (*m == NULL && *s == NULL) {
        n = j - i + 1;
        if (n < 2) return -1;//至少两个矩阵
        *m = new int *[n];
        *s = new int *[n];
        for (int i = 0; i < n; i++) {//生成m, s对应的二维数组
            (*m)[i] = new int[n];
            (*s)[i] = new int[n];
        }
        //初始化
        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                (*m)[i][j] = (*s)[i][j] = -1;
    }
    for (int k = i; k < j; k++) {
        q = recursive_matric_optimal(p, m, s, i, k) + recursive_matric_optimal(p, m, s, k + 1, j) + p[i] * p[k + 1] * p[j + 1];
        if ((*m)[i][j] == -1 || q < (*m)[i][j]) {
            (*m)[i][j] = q;
            (*s)[i][j] = k;
        }
    }
    return (*m)[i][j];
}

matric_show_optimal函数，生成动态规划后的结果，直观看得出哪个矩阵先乘，时间最短。

void matric_show_optimal(int **s, int i, int j) {
    if (i == j)
        printf("A:%d", i);
    else {
        printf("(");
        matric_show_optimal(s, i, s[i][j]);
        matric_show_optimal(s, s[i][j] + 1, j);
        printf(")");
    }
}

数据录入

A0 30x35 
A1 35x15
A2 15x5 
A3 5x10 
A4 10x20
A5 20x25

转换为数组p

int p[] = { 30,35,15,5,10,20,25 };//A(i)的维数表示p(i) x p(i+1)

结果图

这个结果对应书上的结果图（书上旋转了），是一样的

 

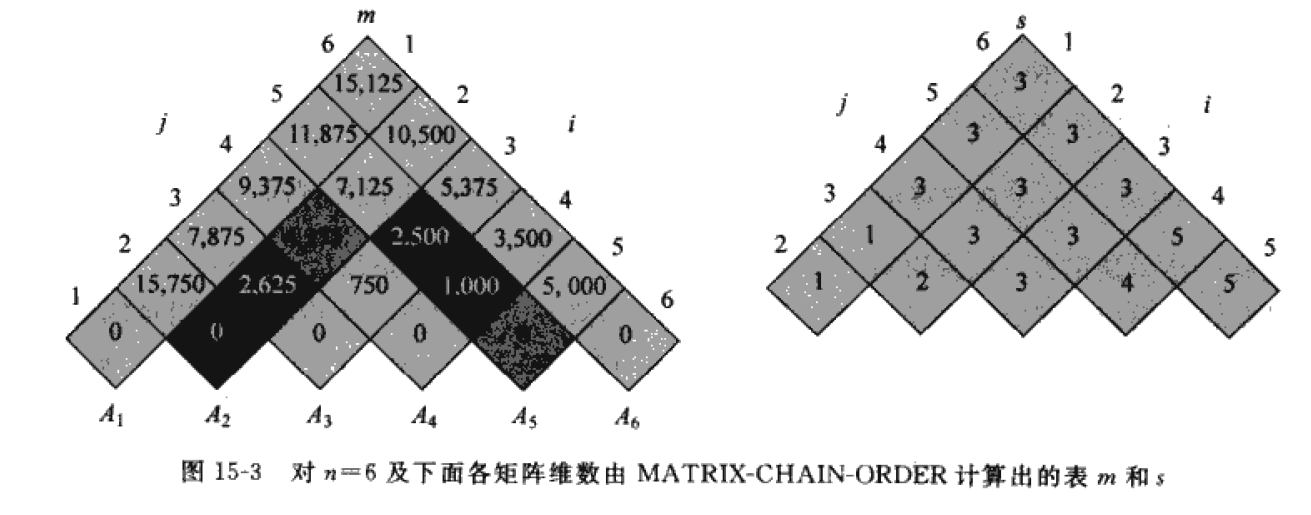
所有代码均经过测试，结果正确！！！