机器学习考试总结

哈工大研究生机器学习考试，个人感觉这些东西没什么用。所以最短时间内会做题了就行。。。

目测几套试卷(19,17,16,14,10,08)知识点如下：

一共八道题，第一题必考候选消除算法，有一题出aq，gs，id3中的某一个，一题出神经网络相关(反向传播算法)，一题出遗传算法，有一题出强化学习，剩下三题会在 knn，kmeans，样例空间，扩张矩阵，贝叶斯，foli算法中出现。

第一题

必考候选消除算法

(1)将G集合初始化为极大一般假设，将S集合初始化为极大特殊假设。

(2)接收一个新的训练例子。如果是正例，则首先由G中去掉不覆盖新正例的概念，然后修改S为由新正例和S原有元素共同归纳出的最特殊的结果(这就是尽量少修改S，但要求S覆盖新正例)。如果这是反例，则首先由S中去掉覆盖该反例的概念，然后修改G为由新反例和G原有元素共同作特殊化的最一般的结果(这就是尽量少修改G，但要求G不覆盖新反例)。

例题(1)：

 

① 把S集合初始化为H中极大特殊假设：S₀=<Ø,Ø,Ø,Ø,Ø,Ø>.    把G集合初始化为H中极大一般假设：G₀=<?,?,?,?,?,?>

②读取第一条数据

S1=<sunny,warm,Normal,strong,warm,same>,   G1=<?,?,?,?,?,?>

   读取第二条数据。 正例

S2=<sunny,warm,?,strong,warm,same>,   G2=<?,?,?,?,?,?>

   读取第三条数据。反例

S3=<sunny,warm,?,strong,warm,same>,   G3={<sunny,?,?,?,?,?>,<?,warm,?,?,?,?>,<?,?,?,?,?,Same>}

   读取第四条数据。正例

S4=<sunny,warm,?,strong,?,?>,   G4={<sunny,?,?,?,?,?>,<?,warm,?,?,?,?>}

③变形空间所有假设为：

{<sunny,warm,?,strong,?,?>,<sunny,warm,?,?,?,?>,<sunny,?,?,?,strong,?>,<?,warm,?,strong,?,?>,<sunny,?,?,?,?,?>,<?,warm,?,?,?,?>}

特殊边界为：S=<sunny,warm,?,strong,?,?> 一般边界为：G={<sunny,?,?,?,?,?>,<?,warm,?,?,?,?>}

例题(2)（19年考试题）：

 

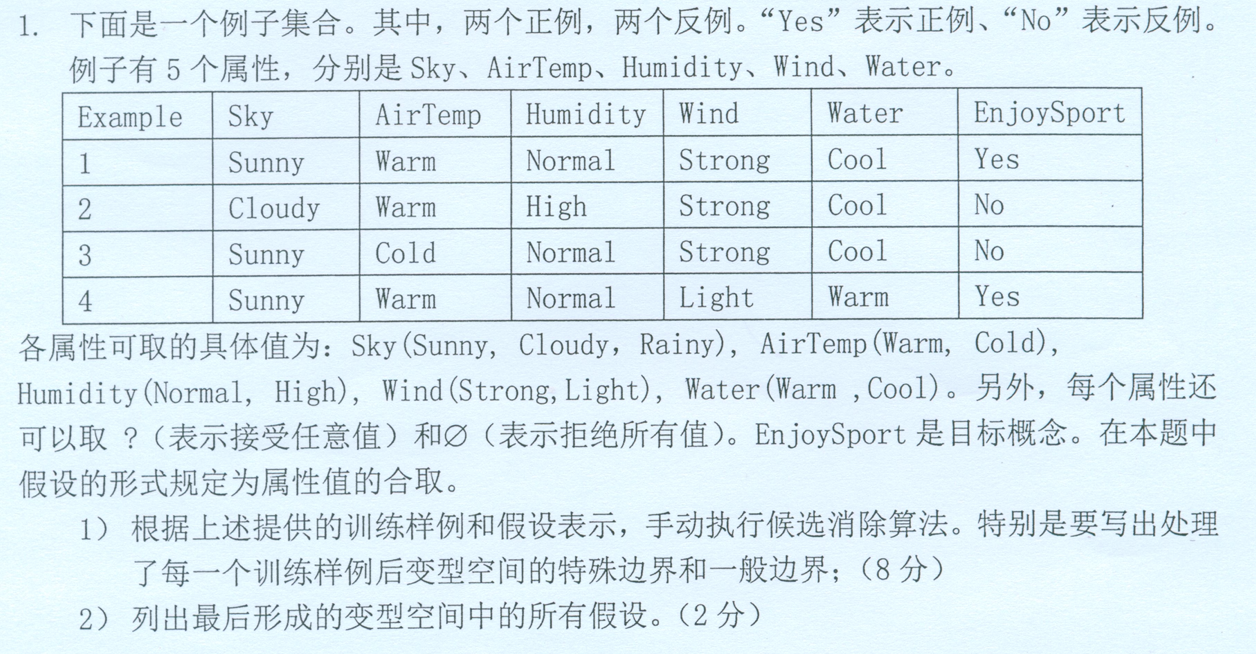
① 把S集合初始化为H中极大特殊假设：S₀=<Ø,Ø,Ø,Ø,Ø>.    把G集合初始化为H中极大一般假设：G₀=<?,?,?,?,?>

②读取第一条数据

S1=<sunny,warm,Normal,strong,cool>,   G1=<?,?,?,?,?>

   读取第二条数据。 反例

S2=<sunny,warm,Normal,strong,cool>,   G2={<sunny,?,?,?,?>,<?,?,normal,?,?>}

   读取第三条数据。反例

S3=<sunny,warm,Normal,strong,cool>,   G3={<sunny,warm,?,?,?>,<?,warm,normal,?,?>}

   读取第四条数据。正例

S4=<sunny,warm,Normal,？,？>,   G4={<sunny,warm,?,?,?>,<?,warm,normal,?,?>}

③变形空间所有假设为：

{<sunny,warm,Normal,？,？>,<sunny,warm,?,?,?>,<?,warm,normal,?,?>}

特殊边界为：S=<sunny,warm,Normal,？,？> 一般边界为：G={<sunny,warm,?,?,?>,<?,warm,normal,?,?>}

例题(3)（17年考试题）：

 

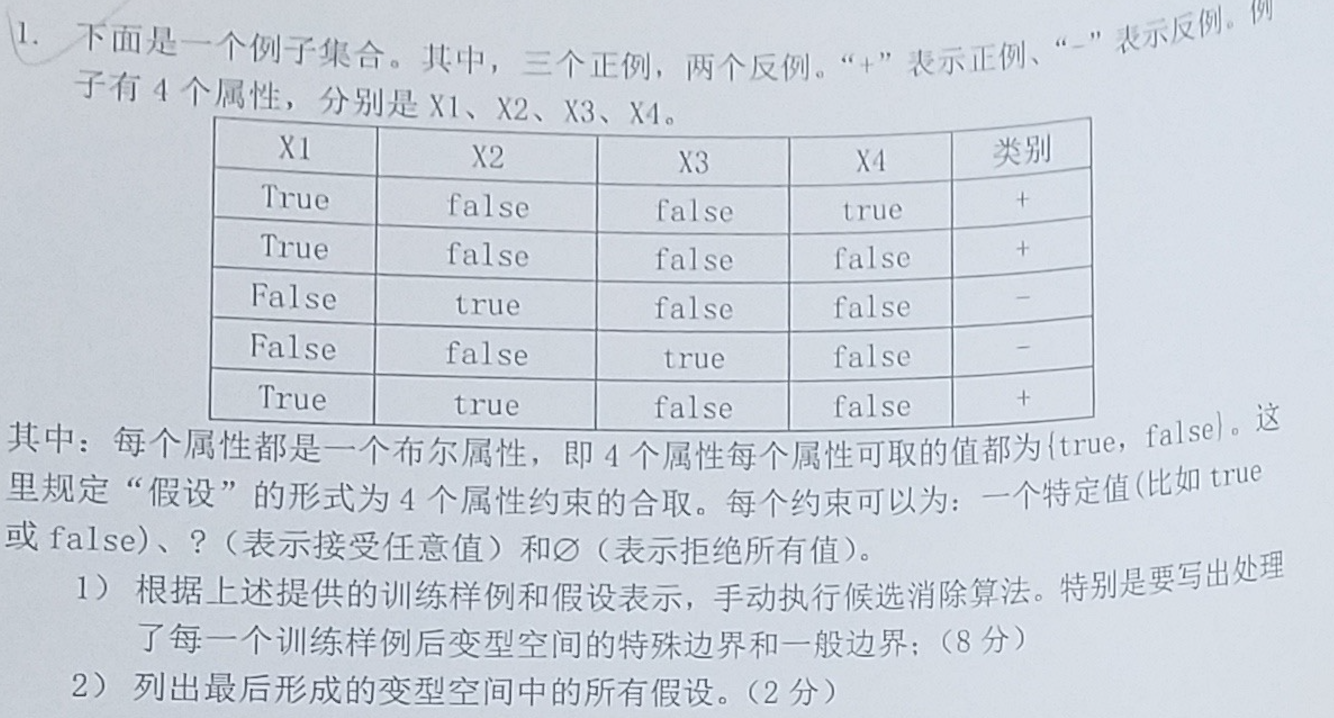
① 把S集合初始化为H中极大特殊假设：S₀=<Ø,Ø,Ø,Ø>.    把G集合初始化为H中极大一般假设：G₀=<?,?,?,?>

②读取第一条数据

S1=<1,0,0,1>,   G1=<?,?,?,?>

   读取第二条数据。 正例

S2=<1,0,0,?>,   G2=<?,?,?,?>

   读取第三条数据。反例

S3=<1,0,0,?>,   G3={<1,?,?,?>,<?,0,?,?>}

   读取第四条数据。反例

S4=<1,0,0,?>,   G4={<1,?,?,?>}

   读取第五条数据。正例

S5=<1,?,0,?>,   G5={<1,?,?,?>}

③变形空间所有假设为：

{<1,?,0,?>,<1,?,?,?>}

特殊边界为：S=<1,?,0,?> 一般边界为：G={<1,?,?,?>}

例题(4)（16年考试题）：

 

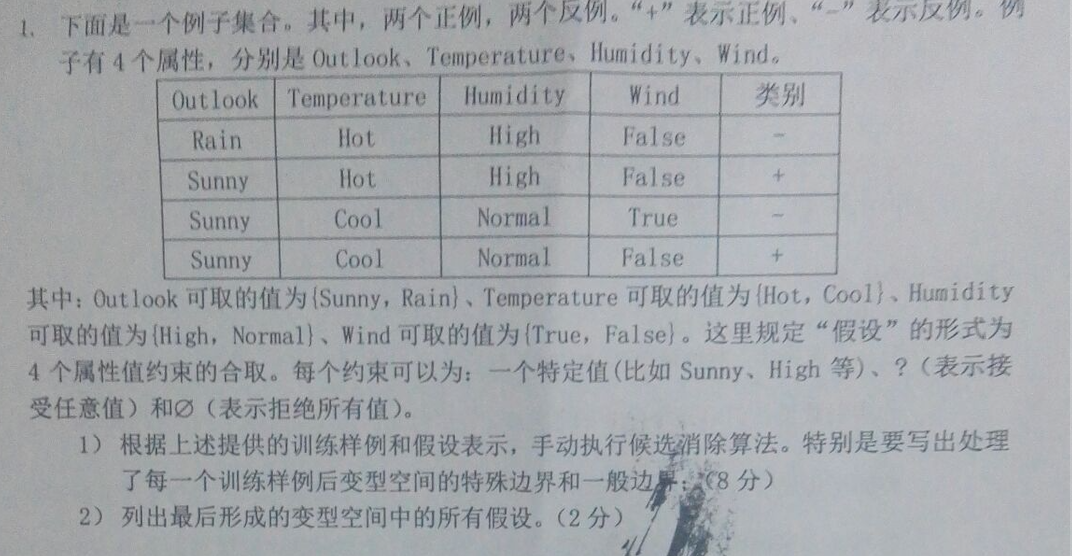
① 把S集合初始化为H中极大特殊假设：S₀=<Ø,Ø,Ø,Ø>.    把G集合初始化为H中极大一般假设：G₀=<?,?,?,?>

②读取第二条数据 正例

S1=<sunny,hot,high,false>,   G1={<?,?,?,?>}

   读取第一条数据。 反例

S2=<sunny,hot,high,false>,   G2=<sunny,?,?,?>

   读取第三条数据。反例

S3=<sunny,hot,high,false>,   G3={<sunny,hot,?,?>,<sunny,?,high,?>,<sunny,?,?,false>}

   读取第四条数据。正例

S4=<sunny,?,?,false>,   G4={<sunny,?,?,false>}

③变形空间所有假设为：<sunny,?,?,false>

特殊边界为：S=<sunny,?,?,false> 一般边界为：G=<sunny,?,?,false>

例题(5)（14年考试题）：

① 把S集合初始化为H中极大特殊假设：S₀=<Ø,Ø,Ø,Ø,Ø,Ø>.    把G集合初始化为H中极大一般假设：G₀=<?,?,?,?,?,?>

②读取第一条数据

S1=<red,small,round,humid,low,smooth>,   G1=<?,?,?,?,?,?>

   读取第二条数据。 正例

S2=<red,small,?,humid,low,smooth>,   G2=<?,?,?,?,?,?>

   读取第三条数据。反例

S3=<red,small,?,humid,low,smooth>,   G3={<red,?,?,?,?,?>,<?,small,?,?,?,?>}

   读取第四条数据。正例

S4=<red,small,?,humid,?,?>,   G4={<red,?,?,?,?,?>,<?,small,?,?,?,?>}

③变形空间所有假设为：

{<red,small,?,humid,?,?>,<red,?,?,humid,?,?>,<red,small,?,?,?,?>,<red,?,?,?,?,?>,<?,small,?,?,?,?>}

 

第二题

1、ID3算法（简单算法流程，如何在缺省值和过拟合进行改进）

基本流程：

第一步：在数据集D中计算目标属性的信息熵：

第二步：在数据集D中对每一个属性计算，在该属性值确定的条件下的信息熵，也就是条件熵。

第三步，计算信息增益度，该值如果越大，表示目标属性在该参考属性上失去的信息熵越多，那么该属性就越应该在决策树的上层。

第四步，选择信息增益度最大的属性作为当前节点。

第五步，将已经选择的参考属性从参考属性列表A中剔除，针对第四步中产生的子数据集D_i再从第一步迭代处理。迭代结束条件为：

a、当某种分类中，目标属性只有一个值。

b、当分到某类的时候，目标属性所有值中，某个值的比例达到了阈值(人为控制)结束迭代。

缺省值：

① “最通常值”办法

② 决策树方法: 把未知属性作为“类”，原来的类作为“属性”（课件上的两个方法）

③概率化缺失值（实际用的方法）

对缺失值的样本赋予该属性所有属性值的概率分布,即将缺失值按照其所在属性已知值的相对概率分布来创建决策树。用系数F进行合理的修正计算的信息量,F=数据库中缺失值所在的属性值样本数量去掉缺失值样本数量/数据库中样本数量的总和,即F表示所给属性具有已知值样本的概率。

https://www.cnblogs.com/ljygoodgoodstudydaydayup/p/7418851.html

过拟合：

一种是预剪枝，即在生成决策树的时候就决定是否剪枝。另一个是后剪枝，即先生成决策树，再通过交叉验证来剪枝。（1：删除以此结点为根的子树。2：使其成为叶子结点。3：赋予该结点关联的训练数据的最常见分类。4：当修剪后的树对于验证集合的性能不会比原来的树差时，才真正删除该结点。)

2、GS算法（手动执行过程，写出算法流程，过拟合问题，缺省值问题）

基本流程：

输入： 例子集；

输出： 规则；

原则： （a) 从所有属性值中选出覆盖正例最多的属性值；

            (b) 在覆盖正例数相同的情况下，优先选择覆盖反例少的属性值；

设PE,NE是正例，反例的集合。PE’,NE’是临时正，反例集。CPX表示公式，F表示规则（概念描述。

(1)F←false;

(2)PE’ ←PE, NE’ ←NE, CPX←true;

(3)按上述(a) (b)两原则选出一个属性值V₀, 设V₀为第j₀个属性的取值，CPX←CPX∧ [Xj₀=V₀]

(4)PE’ ← CPX覆盖的正例，NE’ ← CPX覆盖的反例，如果NE’不为空，转(3);否则，继续执行(5); 

(5) PE←PE\PE’, F ←F ∨CPX, 如果PE= 空   ,停止，否则转(2); 

例题：

 

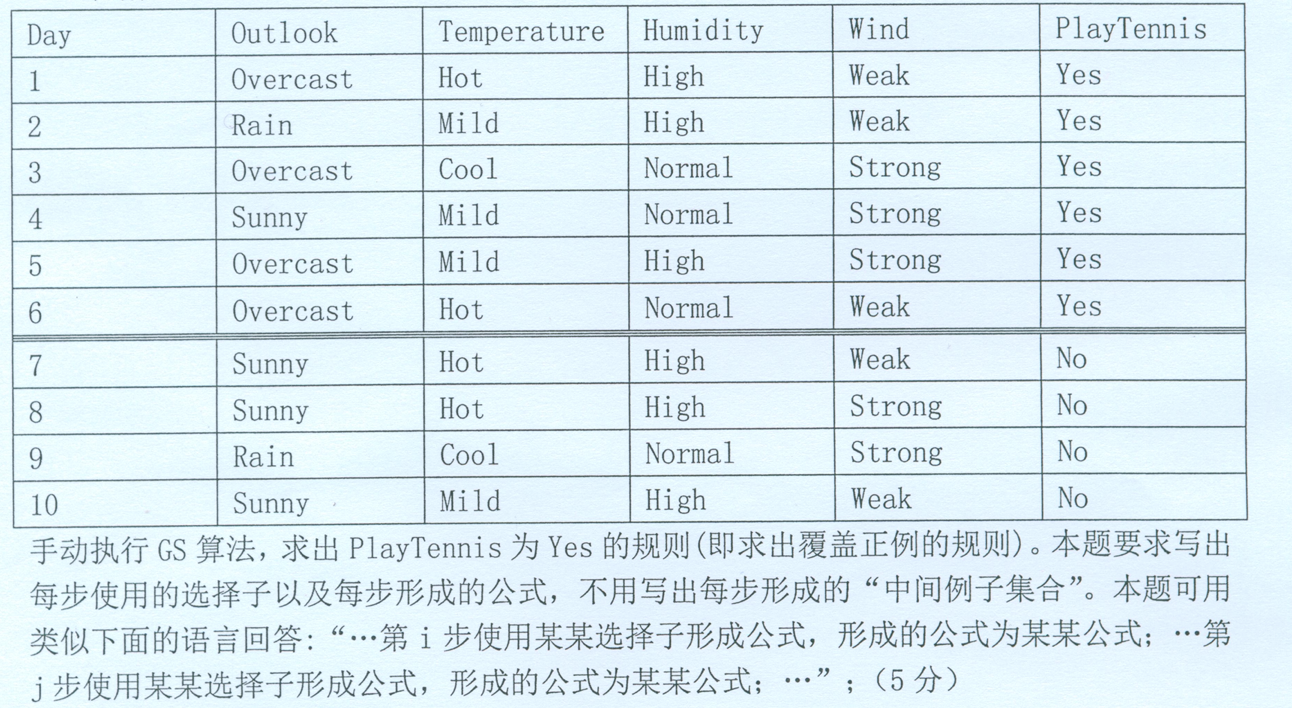
第一步： outlook = Overcast

第二步：temperature = MIld 

第三步：【temperature = MIld 】【outlook=Rain】

第四步：【temperature = MIld 】【hudimity=Normal】

综上：【outlook = Overcast】v【temperature = MIld 】【outlook=Rain】v【temperature = MIld 】【hudimity=Normal】

2、AQ算法（手动执行过程，写出算法流程）

 

 

第三题

强化学习

1、Q学习算法过程

对每个s，a初始化表项Q(s,a)=0

观察当前状态s

一直重复做：

     选择一个动作a并执行它

     接收到立即回报r

     观察新状态s‘

     对Q(s,a）更新：

           Q(s,a）<- r+ gama maxQ(s‘,a’）

     s <- s'

2、马尔可夫决策过程中的收敛性

Qn(s,a）在n->+∞ Qn(s,a）收敛到真实的Q（s，a）

证明：