[NOI2005]月下柠檬树

一堆圆台平行光的投影

在草稿纸上画一下，发现对于一个圆，它投影完还是一个半径不变的圆。

定义树的轴在投影平面上经过的点为原点，定一个正方向，建立平面直角坐标系，
能发现，对于一个半径为\(r\)，高度为\(h\)的圆，投影到平面上是圆心坐标为\((cot(\alpha)h, 0)\)，半径为\(r\)的圆

想象有一个水平的平面，竖直向上移，可以把树切出一堆圆，对于这些圆，把它们投影求个并就是答案

对于每个圆台，它一堆圆的并就是先求上下两个面的圆的投影，再对投影求外公切线，围成的图形

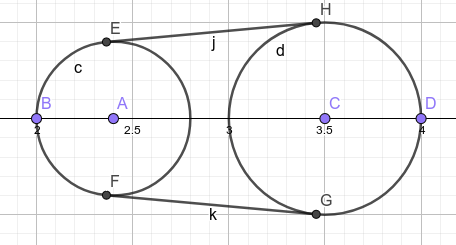
如图，就是\(BEHDGF\)围成的面积

注意对于两个圆的内含或内切关系，是没有切线的

对于树顶，我们把它当做一个半径为\(0\)的圆

那么大概可以画成这样

首先因为它是轴对称的，所以只用算出x轴上方的

但是这面积并怎么求呢？求出所有交点？

这个图挺特殊，所以可以对不规则的函数下方面积考虑使用自适应simpson

然后就做完了

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>

const double eps = 1e-6;
const double STOP = 15;
const int MAXN = 510;
double xs[MAXN], rs[MAXN], theta;
double tx1[MAXN], ty1[MAXN], tx2[MAXN], ty2[MAXN];
int bak;
inline double absx(double x) { return x < 0 ? -x : x; }
inline double sqrx(double x) { return x * x; }
int n;
double f(double at) {
	double res = 0;
	for (int i = 1; i <= n; ++i) {
		double t = absx(xs[i] - at);
		if (t < rs[i])
			res = std::max(res, sqrt(sqrx(rs[i]) - sqrx(t)));
	}
	for (int i = 1; i <= bak; ++i) {
		if (tx1[i] - eps <= at && at <= tx2[i] + eps) {
			double tanx = (ty2[i] - ty1[i]) / (tx2[i] - tx1[i]);
			res = std::max(res, ty1[i] + tanx * (at - tx1[i]));
		}
	}
	return res;
}
inline double calc(double l, double mid, double r) {
	return (l + r + mid * 4) / 6;
}
double simpson(double l, double r, double eps, double ll, double midv, double lr) {
	const double lans = calc(ll, midv, lr) * (r - l);
	const double mid = (l + r) / 2;
	const double lmid = (l + mid) / 2, rmid = (mid + r) / 2;
	const double lmidv = f(lmid), rmidv = f(rmid);
	const double lv = calc(ll, lmidv, midv) * (mid - l);
	const double rv = calc(midv, rmidv, lr) * (r - mid);
	if (absx(lv + rv - lans) <= eps * STOP) return lans;
	return  simpson(l, mid, eps / 2, ll, lmidv, midv) + 
			simpson(mid, r, eps / 2, midv, rmidv, lr);
}
int main() {
	double L = 1e10, R = -1e10;
	scanf("%d%lf", &n, &theta); ++n;
	const double transform = 1 / tanl(theta);
	double now = 0, t;
	for (int i = 1; i <= n; ++i) {
		scanf("%lf", &t);
		now += t;
		xs[i] = now * transform;
	}
	for (int i = 1; i != n; ++i) scanf("%lf", rs + i);
	for (int i = 1; i <= n; ++i) {
		L = std::min(L, xs[i] - rs[i]);
		R = std::max(R, xs[i] + rs[i]);
	}
	rs[n] = 0;
	for (int i = 1; i != n; ++i) {
		if (absx(xs[i] - xs[i + 1]) < absx(rs[i + 1] - rs[i]) + eps) continue;
		const double sina = (rs[i + 1] - rs[i]) / (xs[i + 1] - xs[i]);
		if (1 - sqrx(sina) < eps) continue;
		const double cosa = sqrt(1 - sqrx(sina));
		++bak;
		tx1[bak] = xs[i] - sina * rs[i];
		ty1[bak] = cosa * rs[i];
		tx2[bak] = xs[i + 1] - sina * rs[i + 1];
		ty2[bak] = cosa * rs[i + 1];
	}
	printf("%.2lf\n", simpson(L, R, eps, f(L), f((L + R) / 2), f(R)) * 2);
	return 0;
}